Chapter 6, Problem 6.15P

To determine

The path of minimum time to fix the point.

Answer to Problem 6.15P

The path, here, the point 3 is the lowest point on the curve for the path of the roller coaster car.

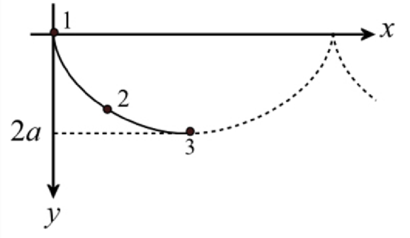
Explanation of Solution

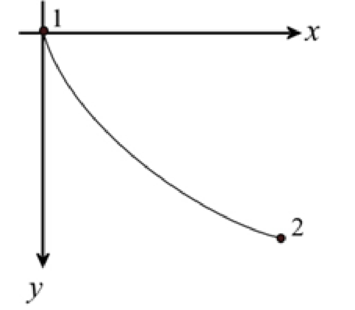
Figure1

The curve for the path of the roller coaster car between the point 1 and 2

Assume that the car is launched at any height $y$ with initial velocity $v_0$ and car reaches the point $2$ with a velocity $v$

At point1

Initial kinetic energy of the car is,

  $K{E}_i=\frac{1}{2}m{v}_0{}^2$

Here, $m$ is the mass of the car.

Initial potential energy of the car is,

  $P{E}_i=mgy$

Here, $g$ is the acceleration due to gravity.

The total initial mechanical energy of the car is the sum of the initial kinetic energy of the car and the initial potential energy of the car. That is

  $E_{\text{total,i}}=P{E}_i+K{E}_i$        (I)

Substitute $\frac{1}{2}m{v}_0{}^2$ for $K{E}_i$ and $mgy$ for $P{E}_i$

  $E_{\text{total,i}}=mgy+\frac{1}{2}m{v}_0{}^2$

At any point between 1 and 2, consider the car is moving with a velocity of $v$ at a height $y^{\prime }$ from the top. The total final mechanical energy of the car is the sum of the final kinetic energy of the car and the final potential energy of the car. That is,

  $\begin{array}{c}{E}_{\text{total,i}}=P{E}_i+K{E}_i\\ =mg\left(y-y^{\prime }\right)+\frac{1}{2}m{v}^2\end{array}$

According to the law of conservation of energy, the total initial mechanical energy of the car is equal to the total final mechanical energy of the car so,

  $\begin{array}{c}mgy+\frac{1}{2}m{v}_0{}^2=mg\left(y-y^{\prime }\right)+\frac{1}{2}m{v}^2\\ \frac{1}{2}m{v}_0{}^2=-mgy+\frac{1}{2}m{v}^2\\ v_0{}^2=-2gy+v^2\\ v=\sqrt{2gy+v_0{}^2}\end{array}$

The expression for unknown path is $x=x\left(y\right)$ thus, the expression for the distance between the neighboring points on the path is,

  $ds=\sqrt{d{x}^2+d{y}^2}$        (II)

The differential form of the variable $x$ as a function of $y$ can be written as,

  $x\text{'}\left(y\right)=\frac{dx}{dy}$

Substitute the equation $dx=x\text{'}\left(y\right)dy$ in equation (II)

  $\begin{array}{c}ds=\sqrt{{\left(x\text{'}\left(y\right)dy\right)}^2+d{y}^2}\\ =\sqrt{\left[{\left(x\text{'}\left(y\right)\right)}^2+1\right]d{y}^2}\\ =\sqrt{\left[{\left(x\text{'}\left(y\right)\right)}^2+1\right]}dy\end{array}$

The expression for the time taken to reach the car from 1 to 2 is,

  $t_{\left(1\to 2\right)}={\displaystyle \underset{1}{\overset{2}{\int }}\frac{ds}{v}}$

Substitute $\sqrt{\left[{\left(x\text{'}\left(y\right)\right)}^2+1\right]}dy$ for $ds$ and $\sqrt{2gy+v_0{}^2}$ for $v$

  $\begin{array}{c}{t}_{\left(1\to 2\right)}={\displaystyle \underset{y_1}{\overset{y_2}{\int }}\frac{\sqrt{\left[{\left(x\text{'}\left(y\right)\right)}^2+1\right]}dy}{\sqrt{2gy+v_0{}^2}}}\\ ={\displaystyle \underset{y_1}{\overset{y_2}{\int }}\frac{\sqrt{\left[{\left(x\text{'}\left(y\right)\right)}^2+1\right]}}{\sqrt{2gy+v_0{}^2}}}dy\end{array}$

Compare this equation with standard form of Euler-Lagrange equation

$S={\displaystyle \underset{x_1}{\overset{x_2}{\int }}f\left[y\left(x\right),y^{\prime }\left(x\right),x\right]}dx$  and the variable $x$ and $y$ are interchanged.

  $f\left(x,x^{\prime },y\right)=\sqrt{\frac{x^{\prime }{\left(y\right)}^2+1}{2gy+v_0{}^2}}$

Write the Euler-Lagrange equation,

  $\frac{\partial f}{\partial x}-\frac{d}{dy}\left(\frac{\partial f}{\partial x^{\prime }}\right)=0$        (III)

Calculate the value of $\frac{\partial f}{\partial x}$ as,

  $\begin{array}{c}\frac{\partial f}{\partial x}=\frac{\partial f}{\partial x}\left(\sqrt{\frac{x^{\prime }{\left(y\right)}^2+1}{2gy+v_0{}^2}}\right)\\ =0\end{array}$

Thus, the Euler-Lagrange equation becomes as,

  $\begin{array}{c}\frac{\partial f}{\partial x}-\frac{d}{dy}\left(\frac{\partial f}{\partial x^{\prime }}\right)=0\\ 0-\frac{d}{dy}\left(\frac{\partial f}{\partial x^{\prime }}\right)=0\\ \frac{d}{dy}\left(\frac{\partial f}{\partial x^{\prime }}\right)=0\\ \frac{\partial f}{\partial x^{\prime }}=C\end{array}$

Substitute $\left(\sqrt{\frac{x^{\prime }{\left(y\right)}^2+1}{2gy+v_0{}^2}}\right)$ for $f$ and $C$ for $\frac{\partial f}{\partial x^{\prime }}$ in expression (III)

  $\begin{array}{l}\frac{\partial f}{\partial x}\left(\sqrt{\frac{x^{\prime }{\left(y\right)}^2+1}{2gy+v_0{}^2}}\right)=C\\ \frac{1}{\sqrt{2gy+v_0{}^2}}\frac{\partial }{\partial x^{\prime }}\left(\sqrt{{x^{\prime }}^2+1}\right)=C\\ \frac{1}{\sqrt{2gy+v_0{}^2}}\frac{2x^{\prime }}{2\sqrt{{x^{\prime }}^2+1}}=C\\ x^{\prime }{\left(x{\text{'}}^2+1\right)}^{-\frac{1}{2}}{\left(2gy+v_0{}^2\right)}^{-\frac{1}{2}}=C\end{array}$        (IV)

But the car raises the height from $y$ to $\frac{v_0{}^2}{2g}$ so the total height raised by the car ot the variable charge in $y$ is,

  $\begin{array}{l}\widehat{y}=y+\frac{v_0{}^2}{2g}\\ 2g\widehat{y}=2gy+v_0{}^2\end{array}$

Substitute $2g\widehat{y}=2gy+v_0{}^2$ in expression (II),

  $\begin{array}{l}{x}^{\prime }{\left(x{\text{'}}^2+1\right)}^{-\frac{1}{2}}{\left(2g\widehat{y}\right)}^{-\frac{1}{2}}=C\\ x^{\prime }{\left(x{\text{'}}^2+1\right)}^{-\frac{1}{2}}{\left(2g\right)}^{-\frac{1}{2}}{\left(\widehat{y}\right)}^{-\frac{1}{2}}=C\\ x^{\prime }{\left(x{\text{'}}^2+1\right)}^{-\frac{1}{2}}{\left(\widehat{y}\right)}^{-\frac{1}{2}}=C^{\prime }\end{array}$

Take the constant as $C^{\prime }={\left(\frac{1}{2a}\right)}^{-\frac{1}{2}}$ and simplify for $x^{\prime }$

  $x^{\prime }{\left({x^{\prime }}^2+1\right)}^{-\frac{1}{2}}{\left(\widehat{y}\right)}^{-\frac{1}{2}}={\left(\frac{1}{2a}\right)}^{\frac{1}{2}}$

Square the equation $x^{\prime }{\left({x^{\prime }}^2+1\right)}^{-\frac{1}{2}}{\left(\widehat{y}\right)}^{-\frac{1}{2}}={\left(\frac{1}{2a}\right)}^{\frac{1}{2}}$ on both sides. And write in terms of $x\text{'}$

  $\begin{array}{l}\frac{{x^{\prime }}^2}{\left(x{\text{'}}^2+1\right)\left(\widehat{y}\right)}=\frac{1}{2a}\\ \left(x{\text{'}}^2+1\right)=\frac{2a}{\widehat{y}}{x^{\prime }}^2\\ \left(\frac{2a-\widehat{y}}{\widehat{y}}\right)x{\text{'}}^2=1\\ x\text{'}=\sqrt{\frac{\widehat{y}}{2a-\widehat{y}}}\end{array}$        (V)

Conclusion:

Let $\widehat{y}=a\left(1-\cos \theta \right)$ , the $d\widehat{y}$ is

  $\begin{array}{c}\frac{d\widehat{y}}{d\theta }=\frac{d}{d\theta }a\left(1-\cos \theta \right)\\ \frac{d\widehat{y}}{d\theta }=\frac{d}{d\theta }\left[\left(a-a\cos \theta \right)\right]\\ \frac{d\widehat{y}}{d\theta }=0-\left[a\left(-\sin \theta \right)\right]\\ =a\sin \theta \end{array}$

Thus, re-write the equation for $d\widehat{y}$

  $d\widehat{y}=a\sin \theta d\theta$

I

Integrate the above expression (V) by substituting , $a\sin \theta d\theta$ for $d\widehat{y}$ and $a\left(1-\cos \theta \right)$ for $\widehat{y}$

  $\begin{array}{l}x={\displaystyle \int \sqrt{\frac{a\left(1-\cos \theta \right)}{2a-a\left(1-\cos \theta \right)}}}a\sin \theta d\theta \\ x={\displaystyle \int \sqrt{\frac{a\left(1-\cos \theta \right)}{2a-a+a\cos \theta }}}a\sin \theta d\theta \\ x={\displaystyle \int \sqrt{\frac{a\left(1-\cos \theta \right)}{a\left(1+\cos \theta \right)}}}a\sin \theta d\theta \\ x={\displaystyle \int \sqrt{\frac{\left(1-\cos \theta \right)\left(1-\cos \theta \right)}{\left(1+\cos \theta \right)\left(1-\cos \theta \right)}}}a\sin \theta d\theta \\ x={\displaystyle \int \sqrt{\frac{{\left(1-\cos \theta \right)}^2}{\left(1-{\cos }^2\theta \right)}}}a\sin \theta d\theta \\ x={\displaystyle \int \frac{\left(1-\cos \theta \right)}{\sin \theta }}a\sin \theta d\theta \\ x=a\left(\theta -\sin \theta \right)+\text{const}\end{array}$

Assume that the initial point represent the origin of the path of the car, that is $\left(x,\widehat{y}\right)=\left(0,0\right)$

Substitute $0$ for $\widehat{y}$ in the equation $\widehat{y}=a\left(1-\cos \theta \right)$

  $\begin{array}{l}0=a\left(1-\cos \theta \right)\\ 0=\left(1-\cos \theta \right)\\ 1=\cos \theta \end{array}$

From the properties of the cosine function, the value of the cosine function is equal to 1 for $\theta =0°$ so the value of $\theta$ is zero.

Substitute $0$ for $x$ , $0°$ for $\theta$ in the equation $x=a\left(\theta -\sin \theta \right)+\text{const}$

  $\begin{array}{l}0=a\left(1-\sin 0°\right)\text{+const}\\ 0=0\text{+const}\\ 0=\text{const}\end{array}$

Thus, the expression $x=a\left(\theta -\sin \theta \right)+\text{const}$ becomes as

  $x=a\left(\theta -\sin \theta \right)+0$

Therefore, the final parametric equation for the path of the car is $x=a\left(\theta -\sin \theta \right)$ and $\widehat{y}=a\left(1-\cos \theta \right)$. These two equations indicate the generals expression for the cycloid through the origin generated by a circular radius $a$ constant of the point $\left(x,\widehat{y}\right)$. The rough curve for the path of roller coaster car between the point 1 and 2 is show below,

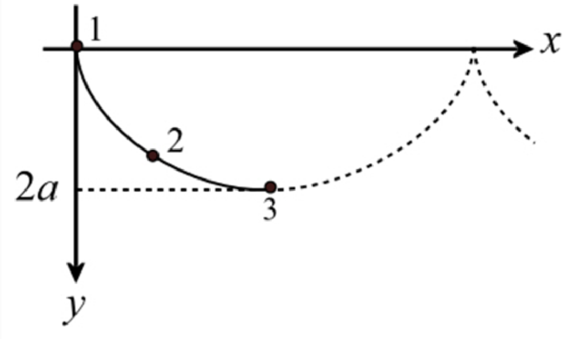
Here, the point 3 is the lowest point on the curve for the path of the roller coaster car.