
A space probe, initially at rest, undergoes an internal mechanical malfunction and breaks into three pieces. One piece of mass ml = 48.0 kg travels in the positive x-direction at 12.0 m/s, and a second piece of mass m2 = 62.0 kg travels in the xy-plane at an angle of 105° at 15.0 m/s. The third piece has mass m3 = 112 kg. (a) Sketch a diagram of the situation, labeling the different masses and their velocities, (b) Write the general expression for conservation of momentum in the x- and y-directions in terms of m1, m2, m3, v1, v2 and v3 and the sines and cosines of the angles, taking θ to be the unknown angle, (c) Calculate the final x-components of the momenta of m1 and m2. (d) Calculate the final y-components of the momenta of m1 and m2. (e) Substitute the known momentum components into the general equations of momentum for the x- and y-directions, along with the known mass m3. (f) Solve the two momentum equations for v3 cos θ and v3 sin θ, respectively, and use the identity cos2 θ + sin2 θ = 1 to obtain v3. (g) Divide the equation for v3 sin θ by that for v3 cos θ to obtain tan θ, then obtain the angle by taking the inverse tangent of both sides, (h) In general, would three such pieces necessarily have to move in the same plane? Why?
a)
Answer to Problem 46P
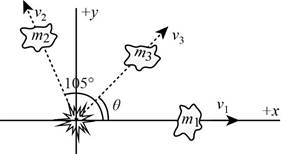
Explanation of Solution
The diagram of the breakage is,
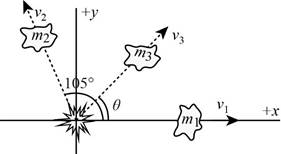
The numerical values of the masses and velocities are,
The numerical values of the masses and velocities are,
Conclusion:
Thus, the diagram of the breakage is,
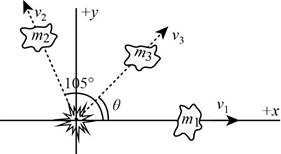
(b)
Answer to Problem 46P
Explanation of Solution
The general expression for the conservation of momentum in x-direction is,
The general expression for the conservation of momentum in y-direction is,
Conclusion:
Thus, the general expression for the conservation of momentum in x-direction is
(c)
Answer to Problem 46P
Explanation of Solution
The final x-component of the momenta of the mass
Substitute
The final x-component of the momenta of the mass
Substitute
Conclusion:
Thus, the final x-component of the momenta of the mass
(d)
Answer to Problem 46P
Explanation of Solution
The final y-component of the momenta of the mass
Substitute
The final y-component of the momenta of the mass
Substitute
Conclusion:
Thus, the final y-component of the momenta of the mass
(e)
Answer to Problem 46P
Explanation of Solution
The final x-component of the momenta of mass
The final y-component of the momenta of mass
Conclusion:
Thus, the final x and y-components of the momenta of mass
(f)
Answer to Problem 46P
Explanation of Solution
In the x-direction,
In the y-direction,
Squaring and adding the equations,
Conclusion:
Thus, the velocity
(g)
Answer to Problem 46P
Explanation of Solution
The tangent of the angle is,
Thus, the angle is,
The angle must be in third quadrant. So, angle
Conclusion:
Thus, the angle
(h)
Answer to Problem 46P
Explanation of Solution
The momentum of the third fragment must be equal in magnitude and must be in the opposite direction to the resultant of the other two fragments momenta. So, all three pieces have to move in the same plane.
Conclusion:
Thus, all three pieces have to move in the same plane.
Want to see more full solutions like this?
Chapter 6 Solutions
College Physics
Additional Science Textbook Solutions
Chemistry: A Molecular Approach (4th Edition)
General, Organic, and Biological Chemistry - 4th edition
MARINE BIOLOGY
Introductory Chemistry (6th Edition)
Organic Chemistry
Fundamentals of Physics Extended
- air is pushed steadily though a forced air pipe at a steady speed of 4.0 m/s. the pipe measures 56 cm by 22 cm. how fast will air move though a narrower portion of the pipe that is also rectangular and measures 32 cm by 22 cmarrow_forwardNo chatgpt pls will upvotearrow_forward13.87 ... Interplanetary Navigation. The most efficient way to send a spacecraft from the earth to another planet is by using a Hohmann transfer orbit (Fig. P13.87). If the orbits of the departure and destination planets are circular, the Hohmann transfer orbit is an elliptical orbit whose perihelion and aphelion are tangent to the orbits of the two planets. The rockets are fired briefly at the depar- ture planet to put the spacecraft into the transfer orbit; the spacecraft then coasts until it reaches the destination planet. The rockets are then fired again to put the spacecraft into the same orbit about the sun as the destination planet. (a) For a flight from earth to Mars, in what direction must the rockets be fired at the earth and at Mars: in the direction of motion, or opposite the direction of motion? What about for a flight from Mars to the earth? (b) How long does a one- way trip from the the earth to Mars take, between the firings of the rockets? (c) To reach Mars from the…arrow_forward
- No chatgpt pls will upvotearrow_forwarda cubic foot of argon at 20 degrees celsius is isentropically compressed from 1 atm to 425 KPa. What is the new temperature and density?arrow_forwardCalculate the variance of the calculated accelerations. The free fall height was 1753 mm. The measured release and catch times were: 222.22 800.00 61.11 641.67 0.00 588.89 11.11 588.89 8.33 588.89 11.11 588.89 5.56 586.11 2.78 583.33 Give in the answer window the calculated repeated experiment variance in m/s2.arrow_forward
- How can i solve this if n1 (refractive index of gas) and n2 (refractive index of plastic) is not known. And the brewsters angle isn't knownarrow_forward2. Consider the situation described in problem 1 where light emerges horizontally from ground level. Take k = 0.0020 m' and no = 1.0001 and find at which horizontal distance, x, the ray reaches a height of y = 1.5 m.arrow_forward2-3. Consider the situation of the reflection of a pulse at the interface of two string described in the previous problem. In addition to the net disturbances being equal at the junction, the slope of the net disturbances must also be equal at the junction at all times. Given that p1 = 4.0 g/m, H2 = 9.0 g/m and Aj = 0.50 cm find 2. A, (Answer: -0.10 cm) and 3. Ay. (Answer: 0.40 cm)please I need to show all work step by step problems 2 and 3arrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning





