Chapter 6, Problem 43P

6-37* to 6-46* For the problem specified in the table, build upon the results of the original problem to determine the minimum factor of safety for fatigue based on infinite life, using the modified Goodman criterion. The shaft rotates at a constant speed, has a constant diameter, and is made from cold-drawn AISI 1018 steel.

Problem Number	Original Problem, Page Number
6-43*	3–74, 152

3-74* In the figure, shaft AB transmits power to shaft CD through a set of bevel gears contacting at point E. The contact force at E on the gear of shaft CD is determined to be (F_E)_CD = –92.8i – 362.8j + 808.0k lbf. For shaft CD: (a) draw a free-body diagram and determine the reactions at C and D assuming simple supports (assume also that bearing C carries the thrust load), (b) draw the shear-force and bending-moment diagrams, (c) for the critical stress element, determine the torsional shear stress, the bending stress, and the axial stress, and (d) for the critical stress element, determine the principal stresses and the maximum shear stress.

To determine

The minimum factor of safety for fatigue based on infinite life.

Answer to Problem 43P

The minimum factor of safety for fatigue based on infinite life is $1.47$.

Explanation of Solution

The free body diagram of the arrangement of shafts is shown in the figure below.

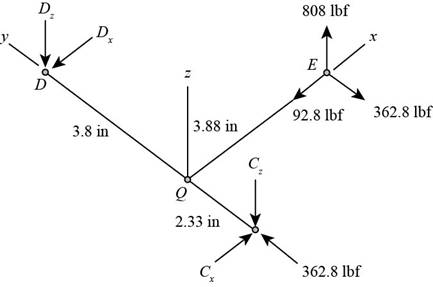
Figure (1)

Write the expression of moment at $D$ in $z\text{-}$ direction.

$\begin{array}{l}{\displaystyle \sum {\left(M_{D1}\right)}_z}=0\\ \left[\begin{array}{l}\left(l_{DQ}+l_{QC}\right)C_x+\left(l_{DQ}\times {\left(F_x\right)}_E\right)\\ +\left(d_E\times {\left(F_y\right)}_E\right)\end{array}\right]=0\\ C_x=\frac{-\left(l_{DQ}\times {\left(F_x\right)}_E\right)-\left(d_E\times {\left(F_y\right)}_E\right)}{\left(l_{DQ}+l_{QC}\right)}\end{array}$ (I)

Here, the reaction at $C$ in $x\text{-}$ direction is $C_x$, the length of the shaft $DQ$ is $l_{DQ}$, the length of the shaft $QC$ is $l_{QC}$, the component of force at $E$ in $x\text{-}$ direction is ${\left(F_x\right)}_E$, the component of force at $E$  in $y\text{-}$ direction is ${\left(F_y\right)}_E$ and the diameter of Bevel gear at $E$ is $d_E$.

Write the expression of moment at $C$ in $z\text{-}$ direction.

$\begin{array}{l}{\displaystyle \sum {\left(M_C\right)}_z}=0\\ \left[\begin{array}{l}\left(l_{DQ}+l_{QC}\right)D_x-\left(l_{QC}\times {\left(F_x\right)}_E\right)\\ +\left(d_E\times {\left(F_y\right)}_E\right)\end{array}\right]=0\\ D_x=\frac{\left(l_{QC}\times {\left(F_x\right)}_E\right)-\left(d_E\times {\left(F_y\right)}_E\right)}{\left(l_{DQ}+l_{QC}\right)}\end{array}$ (II)

Here, the reaction at $D$ in $x\text{-}$ direction is $D_x$.

Write the expression of moment at $D$ in $x\text{-}$ direction.

$\begin{array}{c}{\left({\displaystyle \sum M_D}\right)}_x=0\\ \left(l_{DQ}+l_{QC}\right)C_z-\left(l_{DQ}\times {\left(F_z\right)}_E\right)=0\\ C_z=\frac{\left(l_{DQ}\times {\left(F_z\right)}_E\right)}{\left(l_{DQ}+l_{QC}\right)}\end{array}$ (III)

Here, the reaction at $C$ in $z\text{-}$ direction is $C_z$.

Write the expression of moment at $C$ in $x\text{-}$ direction.

$\begin{array}{l}{\left({\displaystyle \sum M_C}\right)}_x=0\\ \left(l_{DQ}+l_{QC}\right)D_z-\left(l_{QC}\times {\left(F_z\right)}_E\right)=0\\ D_z=\frac{\left(l_{QC}\times {\left(F_z\right)}_E\right)}{\left(l_{DQ}+l_{QC}\right)}\end{array}$ (IV)

Write the expression of net force at $C$ in $y\text{-}$ direction.

$\begin{array}{l}{C}_y+{\left(F_y\right)}_E=0\\ C_y=-{\left(F_y\right)}_E\end{array}$ (V)

Here, the reaction at $C$ in $y\text{-}$ direction is $C_y$.

It is clear from the free body diagram of the shaft $DC$ in Figure (1) that the distance are measured in $y\text{-}$ direction and the reactions are measured in $x\text{-}$ direction and $z\text{-}$ direction. Therefore, the shear force diagram and the bending moment diagram for the shaft $DC$ are made in $x\text{-}$ direction and $z\text{-}$ direction only.

The calculations for shear force diagram in $x\text{-}$ direction on shaft $DC$.

Write the expression of Shear force at $D$ in $x\text{-}$ direction.

$S{F}_{Dx}=-D_x$ (VI)

Here, the shear at $D$ in $x\text{-}$ direction is $S{F}_{Dx}$.

Write the expression of Shear force at $Q$ in $x\text{-}$ direction.

$S{F}_{Qx}=S{F}_{Dx}+{\left(F_x\right)}_E$ (VII)

Here, the shear force at $Q$ in $x\text{-}$ direction is $S{F}_{Qx}$.

Write the expression of Shear force at $C$ in $x\text{-}$ direction.

$S{F}_{Cx}=S{F}_{Qx}+C_x$ (VIII)

Here, the shear force at $C$ in $x\text{-}$ direction is $S{F}_{Cx}$.

The calculations for bending moment diagram in $z\text{-}$ direction on shaft $DC$.

We known that, the bending moment at the supports of the simply supported beam is zero.

Write the bending moment at $D$ and $C$ in $z\text{-}$ direction.

$M_{Cz}=M_{Dz}=0$

Here, the bending moment at $D$ in $z\text{-}$ direction is $M_{Dz}$ and the bending moment at $C$ in $z\text{-}$ direction is $M_{Cz}$.

Write the expression of bending moment at $Q$ in $z\text{-}$ direction due to shear force at $D$.

$M_{Qz1}=S{F}_{Dx}\times l_{DQ}$ (IX)

Here, the bending moment at $Q$ in $z\text{-}$ direction due to shear force at $D$ is $M_{Qz1}$.

Write the expression of bending moment at $Q$ in $z\text{-}$ direction due to shear force at $C$.

$M_{Qz2}=C_x\times l_{QC}$ (X)

Here, the bending moment at $Q$ in $z\text{-}$ direction due to shear force at $C$ is $M_{Qz2}$.

The calculations for shear force diagram in $z\text{-}$ direction on shaft $DC$.

Write the expression of Shear force at $D$ in $z\text{-}$ direction.

$S{F}_{Dz}=D_z$ (XI)

Here, the shear at $D$ in $z\text{-}$ direction is $S{F}_{Dz}$.

Write the expression of Shear force at $Q$ in $z\text{-}$ direction.

$S{F}_{Qz}=S{F}_{Dz}-{\left(F_z\right)}_E$ (XII)

Here, the shear force at $Q$ in $z\text{-}$ direction is $S{F}_{Qz}$.

Write the expression of Shear force at $C$ in $z\text{-}$ direction.

$S{F}_{Cz}=S{F}_{Qz}+C_z$ (XIII)

Here, the shear force at $C$ in $z\text{-}$ direction is $S{F}_{Cz}$.

We known that, the bending moment at the supports of the simply supported beam is zero.

Write the bending moment at $D$ and $C$ in $x\text{-}$ direction.

$M_{Cx}=M_{Dx}=0$

Here, the bending moment at $D$ in $x\text{-}$ direction is $M_{Dx}$ and the bending moment at $C$ in $x\text{-}$ direction is $M_{Cx}$.

Write the expression of bending moment at $Q$ in $x\text{-}$ direction due to shear force at $D$.

$M_{Qx1}=S{F}_{Dz}\times l_{DQ}$ (XIV)

Here, the bending moment at $Q$ in $x\text{-}$ direction due to shear force at $D$ is $M_{Qx1}$.

It is clear from the bending moment diagram that the critical stress element is located at just right of $Q$, where the bending moment is maximum in both the directions and where torsional and shear stress exists.

Write the expression of maximum torque acting on the shaft $DC$.

$T={\left(F_z\right)}_E\times d_E$ (XV)

Here, the maximum torque acting on the shaft $DC$ is $T$.

Write the expression of maximum bending moment acting on the shaft $DC$.

$M=\sqrt{{\left(M_{Qz2}\right)}^2+{\left(M_{Qx1}\right)}^2}$ (XVI)

Here, the maximum bending moment acting on the shaft $DC$ is $M$.

Write the expression of torsional shear stress for critical stress element.

$\tau =\frac{16T}{\pi d^3}$ (XVII)

Here, the torsional shear stress for critical stress element is $\tau$ and diameter of the shaft is $d$.

Write the expression of bending stress for critical stress element.

${\sigma }_b=\pm \frac{32M}{\pi d^3}$ (XVIII)

Here, the bending stress for critical stress element is ${\sigma }_b$.

Write the expression of axial stress for critical stress element.

${\sigma }_a=-\frac{4F}{\pi d^2}$ (XIX)

Here, the axial stress for critical stress element is ${\sigma }_a$.

Write the expression for von Mises alternating stress.

${{\sigma }^{\prime }}_a={\left({\sigma }_a^2+3{\tau }_a^2\right)}^{\frac{1}{2}}$ (XX)

Here, the amplitude component of the axial stress is ${\sigma }_a$ and the amplitude component of the torsional stress is ${\tau }_a$.

Write the expression for von Mises mid-range stress.

${{\sigma }^{\prime }}_m={\left({\sigma }_m^2+3{\tau }_m^2\right)}^{\frac{1}{2}}$ (XXI)

Here, the mid-range component of the axial stress is ${\sigma }_m$ and the mid-range component of the torsional stress is ${\tau }_m$.

Write the expression for von Mises maximum stress.

${{\sigma }^{\prime }}_{\max }={\left({\sigma }_{\max }^2+3{\tau }_{\max }^2\right)}^{\frac{1}{2}}$ (XXII)

Here, the maximum component of the axial stress is ${\sigma }_m$ and the maximum component of the torsional stress is ${\tau }_m$.

Write the expression for yield factor of safety.

$n_y=\frac{S_y}{\max \left[{{\sigma }^{\prime }}_{\max },{{\sigma }^{\prime }}_m,{{\sigma }^{\prime }}_a\right]}$ (XXIII)

Here, the yield strength of the material is $S_y$.

Write the expression for endurance limit for test specimen.

${S^{\prime }}_e=0.5\left(S_{ut}\right)$ (XXIV)

Here, the minimum tensile strength is $S_{ut}$.

Write the surface factor for the countershaft.

$k_a=a\times S_{ut}^b$ (XXV)

Here, the constants for surface factor are $a$ and $b$.

Write the size factor for the countershaft.

$k_b=0.879d^{-0.107}$ (XXVI)

Write the endurance limit at the critical location of the machine part.

$S_e={S^{\prime }}_e\cdot k_a\cdot k_b$ (XXVII)

Write the modified Goodman equation.

$\frac{1}{n_f}=\frac{{{\sigma }^{\prime }}_a}{S_e}+\frac{{{\sigma }^{\prime }}_m}{S_{ut}}$ (XXVIII)

Here, the fatigue factor of safety is $n_f$.

Conclusion:

Substitute $-92.8\text{lbf}$ for ${\left(F_x\right)}_E$, $3.8\text{in}$ for $l_{DQ}$, $-362.8\text{lbf}$ for ${\left(F_y\right)}_E$ and $3.88\text{in}$ for $d_E$ in the Equation (I).

$\begin{array}{c}{C}_x=\frac{\left(3.8\text{in}\times 92.8\text{lbf}\right)+\left(3.88\text{in}\times 362.8\text{lbf}\right)}{\left(3.8\text{in}+2.33\text{in}\right)}\\ =\frac{352.64\text{lbf}\cdot \text{in}+1407.664\text{lbf}\cdot \text{in}}{6.13\text{in}}\\ =287.16\text{lbf}\\ \approx 287.2\text{lbf}\end{array}$

Substitute $-92.8\text{lbf}$ for ${\left(F_x\right)}_E$, $3.8\text{in}$ for $l_{DQ}$, $-362.8\text{lbf}$ for ${\left(F_y\right)}_E$ and $3.88\text{in}$ for $d_E$ in the Equation (II).

$\begin{array}{c}{D}_x=\frac{-\left(2.33\text{in}\times 92.8\text{lbf}\right)+\left(3.88\text{in}\times 362.5\text{lbf}\right)}{\left(3.8\text{in}+2.33\text{in}\right)}\\ =\frac{-\left(216.224\text{lbf}\cdot \text{in}\right)+\left(1406.5\text{lbf}\cdot \text{in}\right)}{\left(3.8\text{in}+2.33\text{in}\right)}\\ =\frac{1190.276\text{lbf}\cdot \text{in}}{6.13\text{in}}\\ \approx 194.4\text{lbf}\end{array}$

Substitute $808\text{lbf}$ for ${\left(F_z\right)}_E$, $3.8\text{in}$ for $l_{DQ}$ and $2.33\text{in}$ for $l_{QC}$ in the Equation (III).

$\begin{array}{c}{C}_z=\frac{\left(3.8\text{in}\times 808\text{lbf}\right)}{\left(3.8\text{in}+2.33\text{in}\right)}\\ =\frac{3070.4}{6.13}\text{lbf}\\ =500.88\text{lbf}\\ \approx 500.9\text{lbf}\end{array}$

Substitute $808\text{lbf}$ for ${\left(F_z\right)}_E$, $3.8\text{in}$ for $l_{DQ}$ and $2.33\text{in}$ for $l_{QC}$ in the Equation (IV).

$\begin{array}{c}{D}_z=\frac{\left(2.33\text{in}\times 808\text{lbf}\right)}{\left(3.8\text{in}+2.33\text{in}\right)}\\ =\frac{1882.64}{6.13}\text{lbf}\\ \approx 307.1\text{lbf}\end{array}$

Substitute $-362.8\text{lbf}$ for ${\left(F_y\right)}_E$ in the Equation (V).

$C_y=362.8\text{lbf}$

Substitute $194.4\text{lbf}$ for $D_x$ in the Equation (VI).

$S{F}_{Dx}=-194.4\text{lbf}$

Substitute $-194.4\text{lbf}$ for $S{F}_{Dx}$ and $-92.8\text{lbf}$ for ${\left(F_x\right)}_E$ in the Equation (VII).

$\begin{array}{c}S{F}_{Qx}=-194.4\text{lbf}-92.8\text{lbf}\\ =-287.2\text{lbf}\end{array}$

Substitute $-287.2\text{lbf}$ for $S{F}_{Qx}$ and $287.2\text{lbf}$ for $C_x$ in the Equation (VIII).

$\begin{array}{c}S{F}_{Cx}=-287.2\text{lbf}+287.2\text{lbf}\\ =0\text{lbf}\end{array}$

Substitute $-194.4\text{lbf}$ for $M_{Qz1}$ and $3.8\text{in}$ for $l_{DQ}$ in the Equation (IX).

$\begin{array}{c}{M}_{Qz1}=-194.4\text{lbf}\times 3.8\text{in}\\ =-738.72\text{lbf}\cdot \text{in}\\ \approx -738.7\text{lbf}\cdot \text{in}\end{array}$

Substitute $287.2\text{lbf}$ for $C_x$ and $2.33\text{in}$ for $l_{QC}$ in the Equation (X).

$\begin{array}{c}{M}_{Qz2}=287.2\text{lbf}\times 2.33\text{in}\\ =669.176\text{lbf}\cdot \text{in}\\ \approx 669.2\text{lbf}\cdot \text{in}\end{array}$

The figure below shows the shear force and bending moment diagram in $x\text{-}$ direction and bending moment diagram in $z\text{-}$ direction.

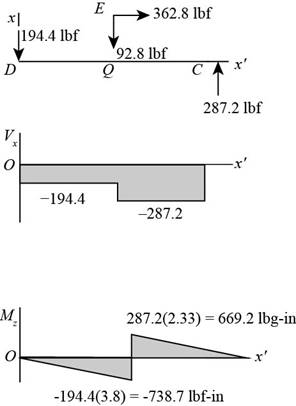
Figure-(2)

Substitute $307.1\text{lbf}$ for $D_z$ in the Equation (XI).

$S{F}_{Dz}=307.1\text{lbf}$

Substitute $307.1\text{lbf}$ for $S{F}_{Dz}$ and $808\text{lbf}$ for ${\left(F_z\right)}_E$ in the Equation (XII).

$\begin{array}{c}S{F}_{Qz}=307.1\text{lbf}-808\text{lbf}\\ =-500.9\text{lbf}\end{array}$

Substitute $-500.9\text{lbf}$ for $S{F}_{Qz}$ and $500.9\text{lbf}$ for $C_z$ in the Equation (XIII).

$\begin{array}{c}S{F}_{Cz}=-500.9\text{lbf}+500.9\text{lbf}\\ =0\text{lbf}\end{array}$

Substitute $307.1\text{lbf}$ for $S{F}_{Dz}$ and $3.8\text{in}$ for $l_{DQ}$ in the Equation (XIV).

$\begin{array}{c}{M}_{Qx1}=307.1\text{lbf}\times 3.8\text{in}\\ =1166.98\text{lbf}\cdot \text{in}\\ \approx 1167\text{lbf}\cdot \text{in}\end{array}$

The figure below shows the shear force and bending moment diagram in $z\text{-}$ direction and bending moment diagram in $x\text{-}$ direction.

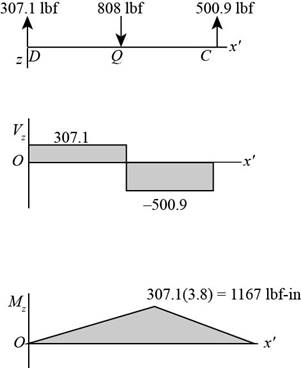
Figure (3)

Substitute $808\text{lbf}$ for ${\left(F_z\right)}_E$ and $3.88\text{in}$ for $d_E$ in the Equation (XV).

$\begin{array}{c}T=808\text{lbf}\times 3.88\text{in}\\ =3135.04\text{lbf}\cdot \text{in}\\ \approx 3135\text{lbf}\cdot \text{in}\end{array}$

Substitute $699.2\text{lbf}\cdot \text{in}$ for $M_{Qz2}$ and $1167\text{lbf}\cdot \text{in}$ for $M_{Qz1}$ in the Equation (XVI).

$\begin{array}{c}M=\sqrt{{\left(669.2\text{lbf}\cdot \text{in}\right)}^2+{\left(1167\text{lbf}\cdot \text{in}\right)}^2}\\ =\sqrt{1809717.64}\text{lbf}\cdot \text{in}\\ =1345.2\text{lbf}\cdot \text{in}\\ \approx 1345\text{lbf}\cdot \text{in}\end{array}$

Substitute $3135\text{lbf}\cdot \text{in}$ for $T$ and $1.13\text{in}$ for $d$ in the Equation (XVII).

$\begin{array}{c}\tau =\frac{16\times 3135\text{lbf}\cdot \text{in}}{\pi {\left(1.13\text{in}\right)}^3}\\ =\frac{50160\text{lbf}\cdot \text{in}}{4.533{\text{in}}^3}\left(\frac{1\text{psi}}{1\text{lbf}/{\text{in}}^2}\right)\\ \approx 11065.5\text{psi}\end{array}$

Substitute $1345\text{lbf}\cdot \text{in}$ for $M$ and $1.13\text{in}$ for $d$ in the Equation (XVIII).

$\begin{array}{c}{\sigma }_b=\pm \frac{32\times 1345}{\pi \times {\left(1.13\right)}^3}\\ =\pm 9494.8\text{psi}\\ \approx \pm 9495\text{psi}\end{array}$

Substitute $362.8\text{lbf}$ for $F$ and $1.13\text{in}$ for $d$ in the Equation (XIX).

$\begin{array}{c}{\sigma }_a=-\frac{4\times 362.8\text{lbf}}{\pi {\left(1.13\text{in}\right)}^2}\\ =\frac{1451.2\text{lbf}}{4.011{\text{in}}^2}\left(\frac{1\text{psi}}{1\text{lbf}/{\text{in}}^2}\right)\\ =-361.7\text{psi}\left(\frac{1\text{kpsi}}{1000\text{psi}}\right)\\ \approx -0.362\text{kpsi}\end{array}$

Substitute $9.495\text{kpsi}$ for ${\sigma }_a$, and $0$ for ${\tau }_a$ in Equation (XX).

$\begin{array}{c}{{\sigma }^{\prime }}_a={\left[{\left(9.495\text{kpsi}\right)}^2+3{\left(0\right)}^2\right]}^{\frac{1}{2}}\\ ={\left[{\left(9.495\text{kpsi}\right)}^2\right]}^{\frac{1}{2}}\\ =9.495\text{kpsi}\end{array}$

Substitute $-0.362\text{kpsi}$ for ${\sigma }_m$, and $11.07\text{kpsi}$ for ${\tau }_a$ in Equation (XXI).

$\begin{array}{c}{{\sigma }^{\prime }}_m={\left[{\left(0.362\text{kpsi}\right)}^2+3{\left(11.07\text{kpsi}\right)}^2\right]}^{\frac{1}{2}}\\ ={\left[0.131{\text{kpsi}}^2+367.6347{\text{kpsi}}^2\right]}^{\frac{1}{2}}\\ =19.177\text{kpsi}\\ \approx 19.18\text{kpsi}\end{array}$

Write the expression for the maximum stress.

${\sigma }_{\max }=-{\sigma }_a+{\sigma }_m$ . (XXIX)

Substitute $-0.362\text{kpsi}$ for ${\sigma }_m$, and $9.495\text{kpsi}$ for ${\sigma }_a$ in Equation (XXIX).

$\begin{array}{c}{\sigma }_{\max }=\left(-9.495\text{kpsi}\right)-0.362\text{kpsi}\\ =9.857\text{kpsi}\end{array}$

Substitute $9.857\text{kpsi}$ for ${\sigma }_{\max }$, and $11.07\text{kpsi}$ for ${\tau }_{\max }$ in Equation (XXII).

$\begin{array}{c}{{\sigma }^{\prime }}_{\max }={\left[{\left(9.857\text{kpsi}\right)}^2+3{\left(11.07\text{kpsi}\right)}^2\right]}^{\frac{1}{2}}\\ ={\left[97.16{\text{kpsi}}^2+367.63{\text{kpsi}}^2\right]}^{\frac{1}{2}}\\ ={\left[464.79{\text{kpsi}}^2\right]}^{\frac{1}{2}}\\ \approx 21.56\text{kpsi}\end{array}$

Refer to the Table A-20 “Deterministic ASTM Minimum Tensile and Yield Strengths for Some Hot-Rolled (HR) and Cold-Drawn (CD) Steels” to obtain the yield strength as $54\text{kpsi}$ and the minimum tensile strength as $64\text{kpsi}$ for AISI 1018 steel.

Substitute $21.56\text{kpsi}$ for ${{\sigma }^{\prime }}_{\max }$ and $54\text{kpsi}$ for $S_y$ in Equation (XXIII).

$\begin{array}{c}{n}_y=\frac{54\text{kpsi}}{21.56\text{kpsi}}\\ =2.5\end{array}$

Substitute $64\text{kpsi}$ for $S_{ut}$ in Equation (XXIV).

$\begin{array}{c}{S^{\prime }}_e=0.5\left(64\text{kpsi}\right)\\ =32\text{kpsi}\end{array}$

Refer to Table 6-2 “Parameters for Marin Surface Modification Factor” to obtain $2.7$ as $a$ and $-0.265$ as $b$.

Substitute $2.7$ for $a$, $64$ for $S_{ut}$ and $-0.265$ for $b$ in Equation (XXV).

$\begin{array}{c}{k}_a=2.7{\left(64\right)}^{-0.265}\\ =2.7\times 0.332\\ =0.8964\\ \approx 0.90\end{array}$

Substitute $1.13$ for $d$ in Equation (XXVI).

$\begin{array}{c}{k}_b=0.879{\left(1.13\right)}^{-0.107}\\ =0.879\times 0.987\\ =0.8675\\ \approx 0.87\end{array}$

Substitute $0.87$ for $k_b$, $0.9$ for $k_a$ and $32\text{kpsi}$ for ${S^{\prime }}_e$ in Equation (XXVII).

$\begin{array}{c}{S}_e=0.9\left(0.87\right)\left(32\text{kpsi}\right)\\ =0.783\left(32\text{kpsi}\right)\\ =25.056\text{kpsi}\\ \approx 25.1\text{kpsi}\end{array}$

Substitute $9.495\text{kpsi}$ for ${{\sigma }^{\prime }}_a$, $25.1\text{kpsi}$ for $S_e$, $64\text{kpsi}$ for $S_{ut}$ and $19.18\text{kpsi}$ for ${{\sigma }^{\prime }}_m$ in Equation (XXVIII).

$\begin{array}{c}\frac{1}{n_f}=\frac{9.495\text{kpsi}}{25.1\text{kpsi}}+\frac{19.18\text{kpsi}}{64\text{kpsi}}\\ \frac{1}{n_f}=0.677\\ n_f\approx 1.47\end{array}$

Thus, the minimum factor of safety for fatigue based on infinite life is $1.47$.