
Concept explainers
(a) Draw two typical curves y = f(x) and y = g(x), where f(x) ≥ g(x) for a ≤ x ≤ b. Show how to approximate the area between these curves by a Riemann sum and sketch the corresponding approximating rectangles. Then write an expression for the exact area.
(b) Explain how the situation changes if the curves have equations x = f(y) and x = g(y), where f(y) ≥ g(y) for c ≤ y ≤ d.
(a)
To Draw: the two typical curves y=f(x) and y=g(x).
To define: A Riemann sum that approximates the area between the two typical curves with drawing of the corresponding approximating rectangles and exact area between the two typical curves and the expression for the exact area.
Explanation of Solution
Consider the two curves y=f(x) and y=g(x).
Here, the top curve function is f(x) and the bottom curve function is g(x).
Assume f and g are continuous function and f(x)≥g(x) for a≤x≤b.
Here, the lower limit is a and the upper limit is b.
Show the approximate ith strip rectangle with base Δx and height f(x*i)−g(x*i) in the region between a and b.
Sketch the two typical curves y=f(x) and y=g(x) as shown in Figure 1.
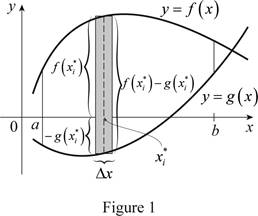
Refer to figure 1.
The two typical curves y=f(x) and y=g(x) showing the approximate ith strip rectangle is drawn.
The expression for the exact area is A=limn→∞n∑i=1[f(x*i)−g(x*i)] Δx.
Divide the area between the two typical curves into n strips of equal width and take the entire sample points to be right endpoints, in which x*i as xi. Hence the Riemann sum is
n∑i=1[f(x*i)−g(x*i)] Δx
Sketch thecorresponding approximating rectangles as shown in Figure 2.
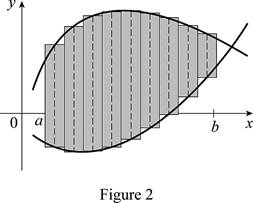
The better and better approximation occurs in n→∞. Hencethe exact areaA, between the two typical curves is the sum of the areas of the corresponding approximating rectangles as shown below.
A=limn→∞n∑i=1[f(x*i)−g(x*i)] Δx
Thus, the Riemann sum with the sketch of corresponding approximating rectangles and the exact area between the two typical curves shown.
Therefore, the approximation of the area between the two typical curves using Riemann sum with the sketch of the corresponding approximating rectangles and the sum of the areas corresponding approximating rectangles is the exact area.
(b)
To Draw: The two typical curves with the changing the situation as x=f(y) and x=g(y).
To define: The situation if the curves changes from y=f(x) and y=g(x) to x=f(y) and x=g(y) the expression for the exact area.
The expression for the exact area is A=∫dc[f(y)−g(y)]dy.
Explanation of Solution
Consider the two curves x=f(y) and x=g(y).
Here, the right curve function is f(y) and the left curve function is g(y).
Assume f and g are continuous function and f(y)≥g(y) for c≤y≤d.
Here, the bottom limit is c and the top limit is d.
Sketch the two typical curves x=f(y) and x=g(y) is shown in Figure 3.
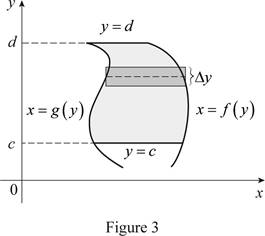
Thus, the two typical curves y=f(x) and y=g(x) are drawn.
Normally the height calculated from the top function minus bottom one and integrating from left to right. Instead of normal calculation, use “right minus left” and integrating from bottom to top. Therefore the exact area, A written as
A=∫dc[f(y)−g(y)]dy
Therefore, the changes of the situation if the curves have equations x=f(y) and x=g(y) is explained.
Want to see more full solutions like this?
Chapter 6 Solutions
Single Variable Calculus: Concepts and Contexts, Enhanced Edition
Additional Math Textbook Solutions
Precalculus: A Unit Circle Approach (3rd Edition)
Pathways To Math Literacy (looseleaf)
Precalculus
Beginning and Intermediate Algebra
Elementary Statistics: Picturing the World (7th Edition)
Calculus: Early Transcendentals (2nd Edition)
- please do Q3arrow_forwardUse the properties of logarithms, given that In(2) = 0.6931 and In(3) = 1.0986, to approximate the logarithm. Use a calculator to confirm your approximations. (Round your answers to four decimal places.) (a) In(0.75) (b) In(24) (c) In(18) 1 (d) In ≈ 2 72arrow_forwardFind the indefinite integral. (Remember the constant of integration.) √tan(8x) tan(8x) sec²(8x) dxarrow_forward
- Find the indefinite integral by making a change of variables. (Remember the constant of integration.) √(x+4) 4)√6-x dxarrow_forwarda -> f(x) = f(x) = [x] show that whether f is continuous function or not(by using theorem) Muslim_mathsarrow_forwardUse Green's Theorem to evaluate F. dr, where F = (√+4y, 2x + √√) and C consists of the arc of the curve y = 4x - x² from (0,0) to (4,0) and the line segment from (4,0) to (0,0).arrow_forward
- Evaluate F. dr where F(x, y, z) = (2yz cos(xyz), 2xzcos(xyz), 2xy cos(xyz)) and C is the line π 1 1 segment starting at the point (8, ' and ending at the point (3, 2 3'6arrow_forwardCan you help me find the result of an integral + a 炉[メをメ +炉なarrow_forward2 a Can you help me find the result of an integral a 아 x² dxarrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





