Elementary Linear Algebra (MindTap Course List)
8th Edition
ISBN: 9781305658004
Author: Ron Larson
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 5.CR, Problem 71CR
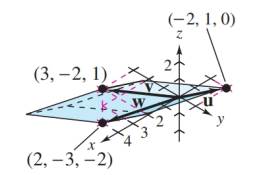
Finding the Volume of a Parallelepiped In Exercises 69-72, find the volume Vof the parallelepiped that has u, v, and was adjacent edges using the formula V=|u⋅(v×w)|.
u=−2i+jv=3i−2j+kw=2i−3j−2k
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
(a)
(b)
(c)
(d)
de
unique?
Answer the following questions related to the linear system
x + y + z = 2
x-y+z=0
2x + y 2 3
rewrite the linear system into the matrix-vector form A = 5
Fuse elementary row operation to solve this linear system. Is the solution
use elementary row operation to find the inverse of A and then solve
the linear system. Verify the solution is the same as (b).
give the null space of matrix A and find the dimension of null space.
give the column space of matrix A and find the dimension of the column
space of A (Hint: use Rank-Nullity Theorem).
please explain in a clear way
Solve questions by Course Name Ordinary Differential Equations
Chapter 5 Solutions
Elementary Linear Algebra (MindTap Course List)
Ch. 5.1 - Finding the Length of a Vector. In Exercises 1-4,...Ch. 5.1 - Finding the Length of a Vector. In Exercises 1-4,...Ch. 5.1 - Finding the Length of a Vector. In Exercises 1-4,...Ch. 5.1 - Finding the Length of a Vector. In Exercises 1-4,...Ch. 5.1 - Finding the Length of a Vector. In Exercises 5-8,...Ch. 5.1 - Finding the Length of a Vector. In Exercises 58,...Ch. 5.1 - Exercises Finding the Length of a Vector In...Ch. 5.1 - Exercises Finding the Length of a Vector In...Ch. 5.1 - Exercises Finding a Unit Vector. In Exercises 912,...Ch. 5.1 - Exercises Finding a Unit Vector. In Exercises 912,...
Ch. 5.1 - Exercises Finding a Unit Vector. In Exercises 912,...Ch. 5.1 - Exercises Finding a Unit Vector. In Exercises 912,...Ch. 5.1 - Exercises Finding a Vector. In Exercises 1316,...Ch. 5.1 - Prob. 14ECh. 5.1 - Prob. 15ECh. 5.1 - Finding a VectorIn Exercises 13-16, find the...Ch. 5.1 - Consider the vector v=(1,3,0,4). Find u such that...Ch. 5.1 - For what values of c is c(1,2,3)=1?Ch. 5.1 - Finding the Distance Between Two VectorsIn...Ch. 5.1 - Finding the Distance Between Two VectorsIn...Ch. 5.1 - Finding the Distance Between Two VectorsIn...Ch. 5.1 - Finding the Distance Between Two VectorsIn...Ch. 5.1 - Prob. 23ECh. 5.1 - Prob. 24ECh. 5.1 - Prob. 25ECh. 5.1 - Prob. 26ECh. 5.1 - Find (u+v)(2uv) when uu=4, uv=5, and vv=10.Ch. 5.1 - Find (3uv)(u3v) when uu=8, uv=7, and vv=6.Ch. 5.1 - Finding Lengths, Unit Vectors, and Dot Products In...Ch. 5.1 - Finding Lengths, Unit Vectors, and Dot Products In...Ch. 5.1 - Finding Lengths, Unit Vectors, and Dot Products In...Ch. 5.1 - Prob. 32ECh. 5.1 - Finding Lengths, Unit Vectors, and Dot Products In...Ch. 5.1 - Prob. 34ECh. 5.1 - Verifying the Cauchy-Schwarz Inequality In...Ch. 5.1 - Verifying the Cauchy-Schwarz Inequality In...Ch. 5.1 - Prob. 37ECh. 5.1 - Prob. 38ECh. 5.1 - Finding the Angle Between Two Vectors In Exercises...Ch. 5.1 - Finding the Angle Between Two Vectors In Exercises...Ch. 5.1 - Prob. 41ECh. 5.1 - Prob. 42ECh. 5.1 - Finding the Angle Between Two Vectors In Exercises...Ch. 5.1 - Finding the Angle Between Two Vectors In Exercises...Ch. 5.1 - Finding the Angle Between Two Vectors In Exercises...Ch. 5.1 - Prob. 46ECh. 5.1 - Determining a Relationship Between Two Vectors In...Ch. 5.1 - Determining a Relationship Between Two Vectors In...Ch. 5.1 - Prob. 49ECh. 5.1 - Determining a Relationship Between Two Vectors In...Ch. 5.1 - Prob. 51ECh. 5.1 - Determining a Relationship Between Two Vectors In...Ch. 5.1 - Exercises Determining a relationship Between Two...Ch. 5.1 - Prob. 54ECh. 5.1 - Prob. 55ECh. 5.1 - Exercises Finding orthogonal Vectors In Exercises...Ch. 5.1 - Exercises Finding orthogonal Vectors In Exercises...Ch. 5.1 - Prob. 58ECh. 5.1 - Prob. 59ECh. 5.1 - Verifying the Triangle Inequality. In Exercises...Ch. 5.1 - Prob. 61ECh. 5.1 - Prob. 62ECh. 5.1 - Prob. 63ECh. 5.1 - Verifying the Pythagorean Theorem In Exercises...Ch. 5.1 - Prob. 65ECh. 5.1 - Prob. 66ECh. 5.1 - Rework Exercise 23 using matrix multiplication....Ch. 5.1 - Rework Exercise 24 using matrix multiplication....Ch. 5.1 - Prob. 69ECh. 5.1 - Prob. 70ECh. 5.1 - Writing In Exercises 71 and 72, determine whether...Ch. 5.1 - Prob. 72ECh. 5.1 - True or False?In Exercises 73 and 74, determine...Ch. 5.1 - Prob. 74ECh. 5.1 - Prob. 75ECh. 5.1 - Prob. 76ECh. 5.1 - Orthogonal Vectors In Exercises 77 and 78, let...Ch. 5.1 - Orthogonal Vectors In Exercises 77 and 78, let...Ch. 5.1 - Prob. 79ECh. 5.1 - Prob. 80ECh. 5.1 - Prob. 81ECh. 5.1 - Prob. 82ECh. 5.1 - Guided Proof Prove that if u is orthogonal to v...Ch. 5.1 - Prob. 84ECh. 5.1 - Prob. 85ECh. 5.1 - Proof Prove that u+v=u+v if and only if u and v...Ch. 5.1 - Proof Use the properties of matrix multiplication...Ch. 5.1 - Prob. 88ECh. 5.1 - Writing Let x be a solution to mn homogeneous...Ch. 5.2 - Showing That a Function Is an Inner Product In...Ch. 5.2 - Showing That a Function Is an Inner Product In...Ch. 5.2 - Showing That a Function Is an Inner Product In...Ch. 5.2 - Showing That a Function Is an Inner Product In...Ch. 5.2 - Showing That a Function Is an Inner Product In...Ch. 5.2 - Showing That a Function Is an Inner Product In...Ch. 5.2 - Showing That a Function Is an Inner Product In...Ch. 5.2 - Showing That a Function Is an Inner ProductIn...Ch. 5.2 - Showing That a Function Is Not an Inner Product In...Ch. 5.2 - Showing That a Function Is Not an Inner Product In...Ch. 5.2 - Showing That a Function Is Not an Inner Product In...Ch. 5.2 - Showing That a Function Is Not an Inner Product In...Ch. 5.2 - Showing That a Function Is Not an Inner Product In...Ch. 5.2 - Showing That a Function Is Not an Inner Product In...Ch. 5.2 - Showing That a Function Is Not an Inner Product In...Ch. 5.2 - Prob. 16ECh. 5.2 - Finding Inner Product, Length, and DistanceIn...Ch. 5.2 - Prob. 18ECh. 5.2 - Finding Inner Product, Length, and DistanceIn...Ch. 5.2 - Finding Inner Product, Length, and DistanceIn...Ch. 5.2 - Finding Inner Product, Length, and DistanceIn...Ch. 5.2 - Prob. 22ECh. 5.2 - Finding Inner Product, Length, and DistanceIn...Ch. 5.2 - Finding Inner Product, Length, and DistanceIn...Ch. 5.2 - Finding Inner Product, Length, and DistanceIn...Ch. 5.2 - Prob. 26ECh. 5.2 - Showing That a Function Is an Inner ProductIn...Ch. 5.2 - Showing That a Function Is an Inner ProductIn...Ch. 5.2 - Finding Inner Product, Length, and DistanceIn...Ch. 5.2 - Prob. 30ECh. 5.2 - Finding Inner Product, Length, and DistanceIn...Ch. 5.2 - Finding Inner Product, Length, and Distance In...Ch. 5.2 - Showing That a Function Is an Inner Product In...Ch. 5.2 - Prob. 34ECh. 5.2 - Finding Inner Product, Length, and Distance In...Ch. 5.2 - Finding Inner Product, Length, and Distance In...Ch. 5.2 - Finding Inner Product, Length, and Distance In...Ch. 5.2 - Prob. 38ECh. 5.2 - Calculus In Exercises 39-42, use the functions f...Ch. 5.2 - Prob. 40ECh. 5.2 - Calculus In Exercises 39-42, use the functions f...Ch. 5.2 - Prob. 42ECh. 5.2 - Finding the Angle Between Two Vectors In Exercises...Ch. 5.2 - Finding the Angle Between Two Vectors In Exercises...Ch. 5.2 - Finding the Angle Between Two Vectors In Exercises...Ch. 5.2 - Finding the Angle Between Two Vectors In Exercises...Ch. 5.2 - Finding the Angle Between Two Vectors In Exercises...Ch. 5.2 - Prob. 48ECh. 5.2 - Finding the Angle Between Two Vectors In Exercises...Ch. 5.2 - Finding the Angle Between Two Vectors In Exercises...Ch. 5.2 - Prob. 51ECh. 5.2 - Prob. 52ECh. 5.2 - Prob. 53ECh. 5.2 - Verifying Inequalities In Exercises 53-64, verify...Ch. 5.2 - Prob. 55ECh. 5.2 - Prob. 56ECh. 5.2 - Prob. 57ECh. 5.2 - Prob. 58ECh. 5.2 - Prob. 59ECh. 5.2 - Verifying Inequalities In Exercises 53-64, verify...Ch. 5.2 - Verifying InequalitiesIn Exercises 53-64, verify a...Ch. 5.2 - Prob. 62ECh. 5.2 - Prob. 63ECh. 5.2 - Prob. 64ECh. 5.2 - Calculus In Exercises 65-68, show that f and g are...Ch. 5.2 - Prob. 66ECh. 5.2 - Calculus In Exercises 65-68, show that f and g are...Ch. 5.2 - Prob. 68ECh. 5.2 - Prob. 69ECh. 5.2 - Finding and Graphing Orthogonal Projections in R2...Ch. 5.2 - Prob. 71ECh. 5.2 - Prob. 72ECh. 5.2 - Prob. 73ECh. 5.2 - Finding Orthogonal Projections In Exercises 7376,...Ch. 5.2 - Finding Orthogonal Projections In Exercises 7376,...Ch. 5.2 - Prob. 76ECh. 5.2 - Prob. 77ECh. 5.2 - Calculus In Exercises 77-84, find the orthogonal...Ch. 5.2 - Calculus In Exercises 77-84, find the orthogonal...Ch. 5.2 - Prob. 80ECh. 5.2 - Prob. 81ECh. 5.2 - Prob. 82ECh. 5.2 - Prob. 83ECh. 5.2 - Prob. 84ECh. 5.2 - True or false?In Exercises 85 and 86, determine...Ch. 5.2 - Prob. 86ECh. 5.2 - Prob. 87ECh. 5.2 - Prob. 88ECh. 5.2 - Prob. 89ECh. 5.2 - Proof Let u and v be a nonzero vectors in an inner...Ch. 5.2 - Prob. 91ECh. 5.2 - Prob. 92ECh. 5.2 - Prob. 93ECh. 5.2 - Prob. 94ECh. 5.2 - Guided proofLet u,v be the Euclidean inner product...Ch. 5.2 - CAPSTONE (a) Explain how to determine whether a...Ch. 5.2 - Prob. 97ECh. 5.2 - Prob. 98ECh. 5.2 - Prob. 99ECh. 5.2 - Prob. 100ECh. 5.2 - Consider the vectors u=(6,2,4) and v=(1,2,0) from...Ch. 5.3 - Orthogonal and Orthonormal SetsIn Exercises 1-12,...Ch. 5.3 - Orthogonal and Orthonormal Sets In Exercises 1-12,...Ch. 5.3 - Prob. 3ECh. 5.3 - Orthogonal and Orthonormal SetsIn Exercises 1-12,...Ch. 5.3 - Orthogonal and Orthonormal Sets In Exercises 1-12,...Ch. 5.3 - Prob. 6ECh. 5.3 - Orthogonal and Orthonormal SetsIn Exercises 1-12,...Ch. 5.3 - Orthogonal and Orthonormal SetsIn Exercises 1-12,...Ch. 5.3 - Orthogonal and Orthonormal SetsIn Exercises 1-12,...Ch. 5.3 - Prob. 10ECh. 5.3 - Orthogonal and Orthonormal SetsIn Exercises 1-12,...Ch. 5.3 - Prob. 12ECh. 5.3 - Normalizing an Orthogonal Set In Exercises 13-16,...Ch. 5.3 - Prob. 14ECh. 5.3 - Normalizing an Orthogonal Set In Exercises 13-16,...Ch. 5.3 - Prob. 16ECh. 5.3 - Complete Example 2 by verifying that {1,x,x2,x3}...Ch. 5.3 - Prob. 18ECh. 5.3 - Finding a Coordinate Matrix In Exercises 19-24,...Ch. 5.3 - Prob. 20ECh. 5.3 - Finding a Coordinate Matrix In Exercises 19-24,...Ch. 5.3 - Finding a Coordinate Matrix In Exercises 19-24,...Ch. 5.3 - Prob. 23ECh. 5.3 - Finding a Coordinate Matrix In Exercises 19-24,...Ch. 5.3 - Applying the Gram-Schmidt Process In Exercises...Ch. 5.3 - Prob. 26ECh. 5.3 - Prob. 27ECh. 5.3 - Prob. 28ECh. 5.3 - Prob. 29ECh. 5.3 - Prob. 30ECh. 5.3 - Prob. 31ECh. 5.3 - Prob. 32ECh. 5.3 - Prob. 33ECh. 5.3 - Prob. 34ECh. 5.3 - Prob. 35ECh. 5.3 - Prob. 36ECh. 5.3 - Prob. 37ECh. 5.3 - Prob. 38ECh. 5.3 - Applying the Gram-Schmidt Process In Exercises...Ch. 5.3 - Prob. 40ECh. 5.3 - Use the inner product u,v=2u1v1+u2v2 in R2 and...Ch. 5.3 - WritingExplain why the result of Exercise 41 is...Ch. 5.3 - Calculus In Exercises 43-48, let B={1,x,x2} be a...Ch. 5.3 - Prob. 44ECh. 5.3 - Prob. 45ECh. 5.3 - Prob. 46ECh. 5.3 - Prob. 47ECh. 5.3 - Calculus In Exercises 43-48, let B={1,x,x2} be a...Ch. 5.3 - Prob. 49ECh. 5.3 - Prob. 50ECh. 5.3 - Applying the Alternative Form of the Gram-Schmidt...Ch. 5.3 - Prob. 52ECh. 5.3 - Applying the Alternative Form of the Gram-Schmidt...Ch. 5.3 - Prob. 54ECh. 5.3 - Prob. 55ECh. 5.3 - True or False? In Exercises 55 and 56, determine...Ch. 5.3 - Orthonormal Sets in P2In Exercises 57-62, let...Ch. 5.3 - Prob. 58ECh. 5.3 - Prob. 59ECh. 5.3 - Prob. 60ECh. 5.3 - Orthonormal Sets in P2In Exercises 57-62, let...Ch. 5.3 - Orthonormal Sets in P2In Exercises 57-62, let...Ch. 5.3 - Prob. 63ECh. 5.3 - Guided Proof Prove that if w is orthogonal to each...Ch. 5.3 - Prob. 65ECh. 5.3 - Prob. 66ECh. 5.3 - Prob. 67ECh. 5.3 - Prob. 68ECh. 5.3 - Prob. 69ECh. 5.3 - Prob. 70ECh. 5.3 - Prob. 71ECh. 5.4 - Least Squares Regression LineIn Exercises 1-4,...Ch. 5.4 - Prob. 2ECh. 5.4 - Prob. 3ECh. 5.4 - Prob. 4ECh. 5.4 - Prob. 5ECh. 5.4 - Prob. 6ECh. 5.4 - Prob. 7ECh. 5.4 - Prob. 8ECh. 5.4 - Prob. 9ECh. 5.4 - Prob. 10ECh. 5.4 - Prob. 11ECh. 5.4 - Prob. 12ECh. 5.4 - Prob. 13ECh. 5.4 - Prob. 14ECh. 5.4 - Prob. 15ECh. 5.4 - Prob. 16ECh. 5.4 - Prob. 17ECh. 5.4 - Prob. 18ECh. 5.4 - Prob. 19ECh. 5.4 - Projection Onto a Subspace In Exercises 17-20,...Ch. 5.4 - Fundamental Subspaces In Exercises 21-24, find...Ch. 5.4 - Prob. 22ECh. 5.4 - Prob. 23ECh. 5.4 - Prob. 24ECh. 5.4 - Prob. 25ECh. 5.4 - Prob. 26ECh. 5.4 - Finding the Least Squares Solutions In Exercises...Ch. 5.4 - Finding the Least Squares Solution In Exercises...Ch. 5.4 - Prob. 29ECh. 5.4 - Prob. 30ECh. 5.4 - Prob. 31ECh. 5.4 - Prob. 32ECh. 5.4 - Prob. 33ECh. 5.4 - Prob. 34ECh. 5.4 - Prob. 35ECh. 5.4 - Prob. 36ECh. 5.4 - Prob. 37ECh. 5.4 - Prob. 38ECh. 5.4 - Prob. 39ECh. 5.4 - Prob. 40ECh. 5.4 - Prob. 41ECh. 5.4 - Prob. 42ECh. 5.4 - True or false? In Exercises 43and 44, determine...Ch. 5.4 - True or false? In Exercises 43 and 44, determine...Ch. 5.4 - Proof Prove that if S1 and S2 are orthogonal...Ch. 5.4 - Prob. 46ECh. 5.4 - Prob. 47ECh. 5.4 - Prob. 48ECh. 5.5 - Finding the Cross Product In Exercises 1-6, find...Ch. 5.5 - Prob. 2ECh. 5.5 - Prob. 3ECh. 5.5 - Prob. 4ECh. 5.5 - Prob. 5ECh. 5.5 - Prob. 6ECh. 5.5 - Prob. 7ECh. 5.5 - Prob. 8ECh. 5.5 - Prob. 9ECh. 5.5 - Prob. 10ECh. 5.5 - Prob. 11ECh. 5.5 - Prob. 12ECh. 5.5 - Prob. 13ECh. 5.5 - Prob. 14ECh. 5.5 - Prob. 15ECh. 5.5 - Prob. 16ECh. 5.5 - Prob. 17ECh. 5.5 - Prob. 18ECh. 5.5 - Prob. 19ECh. 5.5 - Prob. 20ECh. 5.5 - Prob. 21ECh. 5.5 - Prob. 22ECh. 5.5 - Prob. 23ECh. 5.5 - Prob. 24ECh. 5.5 - Prob. 25ECh. 5.5 - Prob. 26ECh. 5.5 - Prob. 27ECh. 5.5 - Prob. 28ECh. 5.5 - Prob. 29ECh. 5.5 - Prob. 30ECh. 5.5 - Prob. 31ECh. 5.5 - Prob. 32ECh. 5.5 - Prob. 33ECh. 5.5 - Prob. 34ECh. 5.5 - Prob. 35ECh. 5.5 - Prob. 36ECh. 5.5 - Prob. 37ECh. 5.5 - Prob. 38ECh. 5.5 - Prob. 39ECh. 5.5 - Prob. 40ECh. 5.5 - Prob. 41ECh. 5.5 - Prob. 42ECh. 5.5 - Prob. 43ECh. 5.5 - Prob. 44ECh. 5.5 - Prob. 45ECh. 5.5 - Finding the Area of a Parallelogram In Exercises...Ch. 5.5 - Prob. 47ECh. 5.5 - Prob. 48ECh. 5.5 - Finding the Area of a Triangle In Exercises 49 and...Ch. 5.5 - Prob. 50ECh. 5.5 - Prob. 51ECh. 5.5 - Prob. 52ECh. 5.5 - Prob. 53ECh. 5.5 - Prob. 54ECh. 5.5 - Prob. 55ECh. 5.5 - Prob. 56ECh. 5.5 - Prob. 57ECh. 5.5 - Prob. 58ECh. 5.5 - Prob. 59ECh. 5.5 - Prob. 60ECh. 5.5 - Prob. 61ECh. 5.5 - Prob. 62ECh. 5.5 - Prob. 63ECh. 5.5 - Prob. 64ECh. 5.5 - Prob. 65ECh. 5.5 - Prob. 66ECh. 5.5 - Prob. 67ECh. 5.5 - Prob. 68ECh. 5.5 - Prob. 69ECh. 5.5 - Prob. 70ECh. 5.5 - Prob. 71ECh. 5.5 - Prob. 72ECh. 5.5 - Prob. 73ECh. 5.5 - Prob. 74ECh. 5.5 - Finding a Least Squares Approximation In Exercises...Ch. 5.5 - Prob. 76ECh. 5.5 - Prob. 77ECh. 5.5 - Prob. 78ECh. 5.5 - Prob. 79ECh. 5.5 - Prob. 80ECh. 5.5 - Prob. 81ECh. 5.5 - Prob. 82ECh. 5.5 - Prob. 83ECh. 5.5 - Prob. 84ECh. 5.5 - Prob. 85ECh. 5.5 - Prob. 86ECh. 5.5 - Prob. 87ECh. 5.5 - Prob. 88ECh. 5.5 - Prob. 89ECh. 5.5 - Prob. 90ECh. 5.5 - Prob. 91ECh. 5.5 - Prob. 92ECh. 5.5 - Use your schools library, the Internet, or some...Ch. 5.CR - Finding Lengths, Dot Product, and Distance In...Ch. 5.CR - Finding Lengths, Dot Product, and Distance In...Ch. 5.CR - Prob. 3CRCh. 5.CR - Prob. 4CRCh. 5.CR - Finding Lengths, Dot Product, and Distance In...Ch. 5.CR - Finding Lengths, Dot Product, and Distance In...Ch. 5.CR - Finding Lengths, Dot Product, and Distance In...Ch. 5.CR - Finding Lengths, Dot Product, and Distance In...Ch. 5.CR - Prob. 9CRCh. 5.CR - Prob. 10CRCh. 5.CR - Prob. 11CRCh. 5.CR - Prob. 12CRCh. 5.CR - Prob. 13CRCh. 5.CR - Prob. 14CRCh. 5.CR - Prob. 15CRCh. 5.CR - Prob. 16CRCh. 5.CR - Prob. 17CRCh. 5.CR - Prob. 18CRCh. 5.CR - Finding the Angle Between Two VectorsIn Exercises...Ch. 5.CR - Finding the Angle Between Two Vectors In Exercises...Ch. 5.CR - Prob. 21CRCh. 5.CR - Prob. 22CRCh. 5.CR - Prob. 23CRCh. 5.CR - Prob. 24CRCh. 5.CR - For u=(4,32,1) and v=(12,3,1), a find the inner...Ch. 5.CR - For u=(0,3,13) and v=(43,1,3), a find the inner...Ch. 5.CR - Verify the triangle inequality and the...Ch. 5.CR - Prob. 28CRCh. 5.CR - CalculusIn Exercises 29 and 30, a find the inner...Ch. 5.CR - CalculusIn Exercises 29 and 30, a find the inner...Ch. 5.CR - Prob. 31CRCh. 5.CR - Prob. 32CRCh. 5.CR - Finding an Orthogonal ProjectionIn Exercises...Ch. 5.CR - Finding an Orthogonal ProjectionIn Exercises...Ch. 5.CR - Finding an Orthogonal ProjectionIn Exercises...Ch. 5.CR - Finding an Orthogonal ProjectionIn Exercises...Ch. 5.CR - Applying the Gram-Schmidt ProcessIn Exercises...Ch. 5.CR - Prob. 38CRCh. 5.CR - Prob. 39CRCh. 5.CR - Prob. 40CRCh. 5.CR - Let B={(0,2,2),(1,0,2)} be a basis for a subspace...Ch. 5.CR - Repeat Exercise 41 for B={(1,2,2),(1,0,0)} and...Ch. 5.CR - Prob. 43CRCh. 5.CR - Prob. 44CRCh. 5.CR - Calculus In Exercises 43-46, let f and g be...Ch. 5.CR - Calculus In Exercises 43-46, let f and g be...Ch. 5.CR - Find an orthonormal basis for the subspace of...Ch. 5.CR - Find an orthonormal basis for the solution space...Ch. 5.CR - Prob. 49CRCh. 5.CR - Prob. 50CRCh. 5.CR - Prob. 51CRCh. 5.CR - Prob. 52CRCh. 5.CR - Prob. 53CRCh. 5.CR - Let V be an two dimensional subspace of R4 spanned...Ch. 5.CR - Prob. 55CRCh. 5.CR - Prob. 56CRCh. 5.CR - Prob. 57CRCh. 5.CR - Prob. 58CRCh. 5.CR - Prob. 59CRCh. 5.CR - Find the projection of the vector v=[102]T onto...Ch. 5.CR - Find the bases for the four fundamental subspaces...Ch. 5.CR - Prob. 62CRCh. 5.CR - Prob. 63CRCh. 5.CR - Prob. 64CRCh. 5.CR - Finding the Cross Product In Exercises 65-68, find...Ch. 5.CR - Finding the Cross Product In Exercises 65-68, find...Ch. 5.CR - Prob. 67CRCh. 5.CR - Finding the Cross Product In Exercises 65-68, find...Ch. 5.CR - Prob. 69CRCh. 5.CR - Prob. 70CRCh. 5.CR - Finding the Volume of a ParallelepipedIn Exercises...Ch. 5.CR - Prob. 72CRCh. 5.CR - Prob. 73CRCh. 5.CR - Prob. 74CRCh. 5.CR - Finding a Least Approximation In Exercises 75-78,...Ch. 5.CR - Finding a Least Approximation In Exercises 75-78,...Ch. 5.CR - Prob. 77CRCh. 5.CR - Finding a Least Approximation In Exercises 75-78,...Ch. 5.CR - Finding a Least Squares Approximation In Exercises...Ch. 5.CR - Finding a Least Squares Approximation In Exercises...Ch. 5.CR - Prob. 81CRCh. 5.CR - Prob. 82CRCh. 5.CR - Prob. 83CRCh. 5.CR - Prob. 84CRCh. 5.CM - Prob. 1CMCh. 5.CM - Take this test to review the material in Chapters...Ch. 5.CM - Take this test to review the material in Chapters...Ch. 5.CM - Use a software program or a graphing utility to...Ch. 5.CM - Take this test to review the material in Chapters...Ch. 5.CM - Prob. 6CMCh. 5.CM - Prob. 7CMCh. 5.CM - Take this test to review the material in Chapters...Ch. 5.CM - Take this test to review the material in Chapters...Ch. 5.CM - Prob. 10CMCh. 5.CM - Prob. 11CMCh. 5.CM - Prob. 12CMCh. 5.CM - Prob. 13CMCh. 5.CM - Prob. 14CMCh. 5.CM - Prob. 15CMCh. 5.CM - Prob. 16CMCh. 5.CM - Prob. 17CMCh. 5.CM - Prob. 18CMCh. 5.CM - Prob. 19CMCh. 5.CM - Prob. 20CMCh. 5.CM - Prob. 21CMCh. 5.CM - The two matrices A and B are row-equivalent....Ch. 5.CM - Prob. 23CMCh. 5.CM - Prob. 24CM
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.Similar questions
- Determine whether it's true or false and the reasoning is neededarrow_forward1. (20 pts) Determine whether the following statements are true (T) or false (F)? (A reasoning is required.) (1) Let V be the set of all ordered pairs of real numbers. Consider the following addition and scalar multiplication operations on u = u= (u1, u2) and v = (v1, v2): u + v = (U₁ + V₁, U₂ + v₂), ku = (ku₁, u₂). Is V a vector space under the above operations? U2 (2) The set Mmxn of all m×n matrices with the usual operations of addition and scalar multiplication is a vector space. α (3) The dimension of the vector space of all matrices A = [a b] in R2×2 with a+d=0 is 4. (4) The coordinate vector of p(x) = 2-x+x² in P3 relative to the basis S = {1, 1+x, x + x2} is [4 -2 1]. (5) If a 6×4 matrix A has a rank 3, then the dimension of N(A) is 3.arrow_forward5. (20%) The linear transformation L: P3 → P2 defined by L(f(x)) = f'(x)+ f(0). (a) Find the representing matrix A of L with respect to the ordered basis {x2, x, 1} for P3, and the ordered basis {2,1 - x} for P2. (b) Find the coordinates of the f(x) = 2x² +2 in P3 with respect to the ordered basis {x2,-x, 1}, and find the coordinates of L(f(x)) with respect to the ordered basis {2,1-x}arrow_forward
- For the spinner below, assume that the pointer can never lie on a borderline. Find the following probabilities. (enter the probabilities as fractions)arrow_forwardQuestions 1. Identify and describe potential bias in the study. 2. Identify and describe the way in which the selected participants may or may not represent the population as a whole. 3. Identify and describe the possible problems with the end results since the majority will be from females rather than an even split. 4. Identify and describe the possible problems with identifying females as possibly more vulnerable based on the data collected. 5. Identify a possible null hypothesis and problems in how the study might address this null hypothesis. 6. Identify one possible method of improving the study design and describe how it would improve the validity of the conclusions. 7. Identify a second possible method of improving the study design and describe how it would improve the validity of the conclusions.arrow_forwardThe Course Name Real Analysis please Solve questions by Real Analysisarrow_forward
- part 3 of the question is: A power outage occurs 6 min after the ride started. Passengers must wait for their cage to be manually cranked into the lowest position in order to exit the ride. Sine function model: where h is the height of the last passenger above the ground measured in feet and t is the time of operation of the ride in minutes. What is the height of the last passenger at the moment of the power outage? Verify your answer by evaluating the sine function model. Will the last passenger to board the ride need to wait in order to exit the ride? Explain.arrow_forward2. The duration of the ride is 15 min. (a) How many times does the last passenger who boarded the ride make a complete loop on the Ferris wheel? (b) What is the position of that passenger when the ride ends?arrow_forward3. A scientist recorded the movement of a pendulum for 10 s. The scientist began recording when the pendulum was at its resting position. The pendulum then moved right (positive displacement) and left (negative displacement) several times. The pendulum took 4 s to swing to the right and the left and then return to its resting position. The pendulum's furthest distance to either side was 6 in. Graph the function that represents the pendulum's displacement as a function of time. Answer: f(t) (a) Write an equation to represent the displacement of the pendulum as a function of time. (b) Graph the function. 10 9 8 7 6 5 4 3 2 1 0 t 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 -1 -5. -6 -7 -8 -9 -10-arrow_forward
- A power outage occurs 6 min after the ride started. Passengers must wait for their cage to be manually cranked into the lowest position in order to exit the ride. Sine function model: h = −82.5 cos (3πt) + 97.5 where h is the height of the last passenger above the ground measured in feet and t is the time of operation of the ride in minutes. (a) What is the height of the last passenger at the moment of the power outage? Verify your answer by evaluating the sine function model. (b) Will the last passenger to board the ride need to wait in order to exit the ride? Explain.arrow_forwardThe Colossus Ferris wheel debuted at the 1984 New Orleans World's Fair. The ride is 180 ft tall, and passengers board the ride at an initial height of 15 ft above the ground. The height above ground, h, of a passenger on the ride is a periodic function of time, t. The graph displays the height above ground of the last passenger to board over the course of the 15 min ride. Height of Passenger in Ferris Wheel 180 160 140- €120 Height, h (ft) 100 80 60 40 20 0 ך 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Time of operation, t (min) Sine function model: h = −82.5 cos (3πt) + 97.5 where h is the height of the passenger above the ground measured in feet and t is the time of operation of the ride in minutes. What is the period of the sine function model? Interpret the period you found in the context of the operation of the Ferris wheel. Answer:arrow_forward1. Graph the function f(x)=sin(x) −2¸ Answer: y -2π 一元 1 −1 -2 -3 -4+ 元 2πarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:9781305658004
Author:Ron Larson
Publisher:Cengage Learning
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Inner Product Spaces; Author: Jeff Suzuki: The Random Professor;https://www.youtube.com/watch?v=JzCZUx9ZTe8;License: Standard YouTube License, CC-BY