
Concept explainers
The Tautochrone. A problem of interest in the history of mathematics is that of finding the Tautochrone-the curve down which a particle will slide freely under gravity alone, reaching the bottom in the same time regardless of its starting point on the curve. This problem arose in the construction of a clock pendulum whose period is independent of the amplitude of its motion. The Tautochrone was found by Christian Huygens in
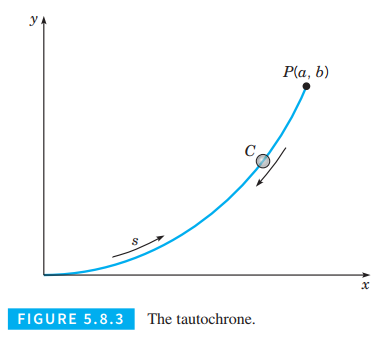
The geometric configuration is shown in Figure
Then it follows from the principle of conservation of energy that the time
(a) Assume that
Then show that
Hint: See Problem 37 of Section 5.1.
(b) Combining Eqs. (i) and (iv), show that
where
(c) Use the substitution
Equations (vi) can be identified as parametric equations of a cycloid. Thus the Tautochrone is an arc of a cycloid.
Want to see the full answer?
Check out a sample textbook solution
Chapter 5 Solutions
DIFFERENTIAL EQUATIONS W/WILEYPLUS
Additional Math Textbook Solutions
Excursions in Modern Mathematics (9th Edition)
Using and Understanding Mathematics: A Quantitative Reasoning Approach (6th Edition)
Finite Mathematics & Its Applications (12th Edition)
Mathematical Ideas (13th Edition) - Standalone book
Calculus for Business, Economics, Life Sciences, and Social Sciences (14th Edition)
Mathematics with Applications In the Management, Natural and Social Sciences (11th Edition)
- A two-stage gear train consists of four gears meshed together (Figure 10). The second and third gears are attached, so that they share the same angular velocity (2=4). Find a formula giving the angular velocity of the fourth gear, 2, in terms of 1 and the values of n1,n2,n3andn4.arrow_forwardBecause the trigonometry functions are periodic, if a basic trigonometric equation has one solution, it has ________several/infinitely many solutions.arrow_forwardThe number of cycles per second of a point in simple harmonic motion is its .arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning, Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning  Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning




