Chapter 5.5, Problem 52AYU

A Rotating Beacon Suppose that a fire truck is parked in front of a building as shown in the figure.

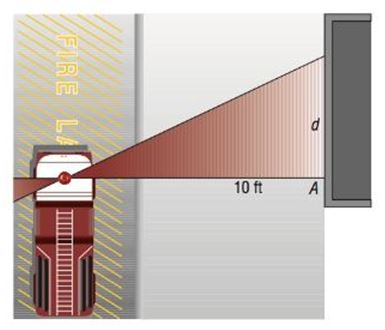
The beacon light on top of the fire truck is located 10 feet from the wall and has a light on each side. If the beacon light rotates 1 revolution every 2 seconds, then a model for determining the distance $d$, in feet, that the beacon of light is from point A on the wall after $t$ seconds is given by

$d\left(t\right)\text{ = }\left|10\tan \left(\pi t\right)\right|$

(a) Graph $d\left(t\right)\text{ = }\left|10\tan \left(\pi t\right)\right|$ for $0\le t\le \text{ 2}$.

(b) For what values of $t$ is the function undefined? Explain what this means in terms of the beam of light on the wall.

(c) Fill in the following table.

(d) Compute $\frac{d\left(0.1\right)-d\left(0\right)}{0.1-0},\frac{d\left(0.2\right)-d\left(0.1\right)}{0.2-0.1}$, and so on, for each consecutive value of $t$. These are called first differences.

(e) Interpret the first differences found in part $\left(d\right)$. What is happening to the speed of the beam of light as $d$ increases?