Chapter 54, Problem 26A

Solve the following exercises based on Principles 18 through 21, although an exercise may require the application of two or more of any of the principles. Where necessary, round linear answers in inches to 3 decimal places and millimeters to 2 decimal places. Round angular answers in decimal degrees to 2 decimal places and degrees and minutes to the nearest minute.

a. If ∠ 1 = 67°00' and ∠ 2 =93°00', find:
(1) $\stackrel{⌢}{AB}$
(2) $\stackrel{⌢}{DE}$
b.If ∠ 1 = 75°00' and ∠ 2 =85°00', find:
(1) $\stackrel{⌢}{AB}$
(2) $\stackrel{⌢}{DE}$

To determine

(a)

The value of arc $\stackrel{⌢}{AB}\text{and}\stackrel{⌢}{DE}$ in the given figure.

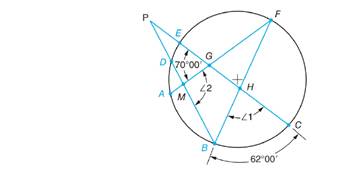
Answer to Problem 26A

The values of arcs AB and DE are $\stackrel{⌢}{AB}=86°00\text{'}$ and $\stackrel{⌢}{DE}=39°00\text{'}$.

Explanation of Solution

Given information:

The value of angle 1 is $\angle 1=67°00\text{'}$

The value of angle 2 is $\angle 2=93°00\text{'}$

The given figure is

  

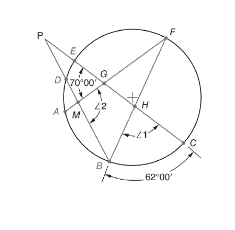
Calculation:

The angles GHF and angle 1 are opposite angles. Thus,

  $\begin{array}{l}\angle GHF=\angle BHC\\ \angle GHF=\angle 1\\ \angle GHF=67°00\text{'}\end{array}$

Similarly, the angles EGM and angle FGH are opposite angles.

  $\begin{array}{l}\angle EGM=\angle FGH\\ 70°00\text{'}=\angle FGH\\ \angle FGH=70°00\text{'}\end{array}$

In triangle FGH, the angle GFH comes out to be

  $\begin{array}{l}\angle GFH+\angle FGH+\angle GHF=180°\\ \angle GFH+70°+67°=180°\\ \angle GFH=180°-\left(70°+67°\right)\\ \angle GFH=43°\end{array}$

Now, an inscribed angle is one half the value of intercepted arc by the angle itself.

  $\begin{array}{l}\angle GFH=\angle AFB=43°00\text{'}\\ \angle AFB=\frac{1}{2}\left(\stackrel{⌢}{AB}\right)\\ \stackrel{⌢}{AB}=2\times \angle AFB\\ \stackrel{⌢}{AB}=2\times 43°00\text{'}\end{array}$

  $\stackrel{⌢}{AB}=86°00\text{'}$

The line PMB is a straight line so,

  $\begin{array}{l}\angle PMG+\angle GMB=180°\\ \angle PMG+93°00\text{'}=180°\\ \angle PMG=87°00\text{'}\end{array}$

Now, in triangle PMG, the sum of all angles should be equal to 180^o.

  $\begin{array}{l}\angle MPG+\angle PGM+\angle PMG=180°\\ \angle MPG+70°00\text{'}+87°00\text{'}=180°\\ \angle MPG=180°-\left(70°00\text{'}+87°00\text{'}\right)\\ \angle MPG=23°00\text{'}\end{array}$

Now, the value of arc DE can be found from the following formula,

  $\begin{array}{l}\angle P=\stackrel{⌢}{BC}-\stackrel{⌢}{DE}\\ 23°00\text{'}=62°00\text{'}-\stackrel{⌢}{DE}\\ \stackrel{⌢}{DE}=62°00\text{'}-23°00\text{'}\end{array}$

  $\stackrel{⌢}{DE}=39°00\text{'}$

The values of arcs AB and DE are $\stackrel{⌢}{AB}=86°00\text{'}$ and $\stackrel{⌢}{DE}=39°00\text{'}$

Conclusion:

Thus, the values of arcs AB and DE are $\stackrel{⌢}{AB}=86°00\text{'}$ and $\stackrel{⌢}{DE}=39°00\text{'}$

To determine

(b)

The value of arc $\stackrel{⌢}{AB}\text{and}\stackrel{⌢}{DE}$ in the given figure.

Answer to Problem 26A

The values of arcs AB and DE are $\stackrel{⌢}{AB}=70°00\text{'}$ and $\stackrel{⌢}{DE}=47°00\text{'}$

Explanation of Solution

Given information:

The value of angle 1 is $\angle 1=75°00\text{'}$

The value of angle 2 is $\angle 2=85°00\text{'}$

The given figure is

  

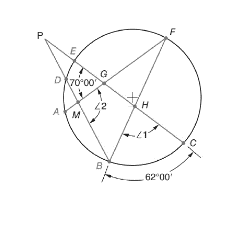
Calculation:

The angles GHF and angle 1 are opposite angles. Thus,

  $\begin{array}{l}\angle GHF=\angle BHC\\ \angle GHF=\angle 1\\ \angle GHF=75°00\text{'}\end{array}$

Similarly, the angles EGM and angle FGH are opposite angles.

  $\begin{array}{l}\angle EGM=\angle FGH\\ 70°00\text{'}=\angle FGH\\ \angle FGH=70°00\text{'}\end{array}$

In triangle FGH, the angle GFH comes out to be

  $\begin{array}{l}\angle GFH+\angle FGH+\angle GHF=180°\\ \angle GFH+70°+75°=180°\\ \angle GFH=180°-\left(70°+75°\right)\\ \angle GFH=35°\end{array}$

Now, an inscribed angle is one half the value of intercepted arc by the angle itself.

  $\begin{array}{l}\angle GFH=\angle AFB=35°00\text{'}\\ \angle AFB=\frac{1}{2}\left(\stackrel{⌢}{AB}\right)\\ \stackrel{⌢}{AB}=2\times \angle AFB\\ \stackrel{⌢}{AB}=2\times 35°00\text{'}\end{array}$

  $\stackrel{⌢}{AB}=70°00\text{'}$

The line PMB is a straight line so,

  $\begin{array}{l}\angle PMG+\angle GMB=180°\\ \angle PMG+85°00\text{'}=180°\\ \angle PMG=95°00\text{'}\end{array}$

Now, in triangle PMG, the sum of all angles should be equal to 180^o.

  $\begin{array}{l}\angle MPG+\angle PGM+\angle PMG=180°\\ \angle MPG+70°00\text{'}+95°00\text{'}=180°\\ \angle MPG=180°-\left(70°00\text{'}+95°00\text{'}\right)\\ \angle MPG=15°00\text{'}\end{array}$

Now, the value of arc DE can be found from the following formula,

  $\begin{array}{l}\angle P=\stackrel{⌢}{BC}-\stackrel{⌢}{DE}\\ 15°00\text{'}=62°00\text{'}-\stackrel{⌢}{DE}\\ \stackrel{⌢}{DE}=62°00\text{'}-15°00\text{'}\end{array}$

  $\stackrel{⌢}{DE}=47°00\text{'}$

The values of arcs AB and DE are $\stackrel{⌢}{AB}=70°00\text{'}$ and $\stackrel{⌢}{DE}=47°00\text{'}$

Conclusion:

Thus, the values of arcs AB and DE are $\stackrel{⌢}{AB}=70°00\text{'}$ and $\stackrel{⌢}{DE}=47°00\text{'}$