
Precalculus
17th Edition
ISBN: 9780078035609
Author: Miller, Julie, Gerken, Donna.
Publisher: Mcgraw-hill Education,
expand_more
expand_more
format_list_bulleted
Concept explainers
Question
Chapter 5.3, Problem 95PE
To determine
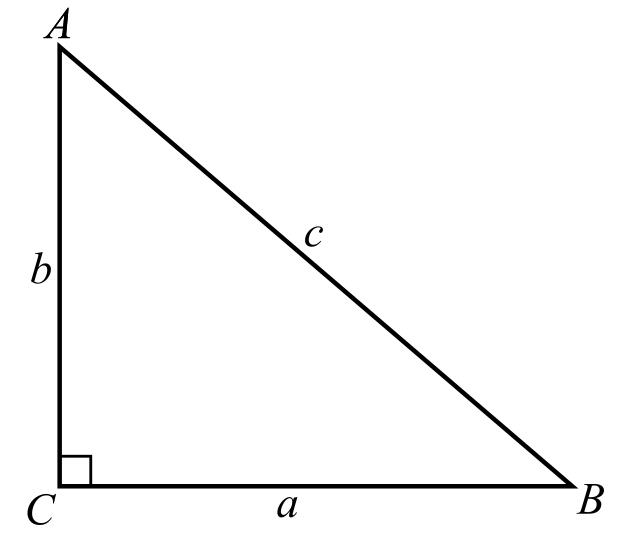
To prove: The identity sin2A=sin2B for a right ΔABC . The given figure is:
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Evaluate the definite integral using the given integration limits and the limits obtained by trigonometric substitution.
14
x²
dx
249
(a) the given integration limits
(b) the limits obtained by trigonometric substitution
Assignment #1
Q1: Test the following series for convergence. Specify the test you use:
1
n+5
(-1)n
a) Σn=o
√n²+1
b) Σn=1 n√n+3
c) Σn=1 (2n+1)3
3n
1
d) Σn=1 3n-1
e) Σn=1
4+4n
answer problem 1a, 1b, 1c, 1d, and 1e and show work/ explain how you got the answer
Chapter 5 Solutions
Precalculus
Ch. 5.1 - Simplify. Write the final form with no fractions....Ch. 5.1 - Simplify. Write the final form with no fractions....Ch. 5.1 - Simplify. Write the final form with no fractions....Ch. 5.1 - Verify that the equation is an identity....Ch. 5.1 - Prob. 5SPCh. 5.1 - Prob. 6SPCh. 5.1 - Verify that the equation is an identity....Ch. 5.1 - Prob. 8SPCh. 5.1 - Prob. 9SPCh. 5.1 - The value tan is the quotient of and , and cot...
Ch. 5.1 - Prob. 2PECh. 5.1 - Given the Pythagorean identitysin2x+cos2x=1 ,...Ch. 5.1 - Given the Pythagorean identity tan2x+1=sec2x ,...Ch. 5.1 - Prob. 5PECh. 5.1 - An equation that is true for all values of the...Ch. 5.1 - For Exercises 7-10, find the least common...Ch. 5.1 - Prob. 8PECh. 5.1 - For Exercises 7-10, find the least common...Ch. 5.1 - Prob. 10PECh. 5.1 - For Exercises 11-12, multiply. a. a+b2 b....Ch. 5.1 - Prob. 12PECh. 5.1 - Prob. 13PECh. 5.1 - Prob. 14PECh. 5.1 - Prob. 15PECh. 5.1 - Prob. 16PECh. 5.1 - Prob. 17PECh. 5.1 - For Exercises 13-20, factor each expression. a....Ch. 5.1 - Prob. 19PECh. 5.1 - Prob. 20PECh. 5.1 - Prob. 21PECh. 5.1 - For Exercises 21-36, simplify the expression....Ch. 5.1 - For Exercises 21-36, simplify the expression....Ch. 5.1 - For Exercises 21-36, simplify the expression....Ch. 5.1 - For Exercises 21-36, simplify the expression....Ch. 5.1 - For Exercises 21-36, simplify the expression....Ch. 5.1 - For Exercises 21-36, simplify the expression....Ch. 5.1 - For Exercises 21-36, simplify the expression....Ch. 5.1 - For Exercises 21-36, simplify the expression....Ch. 5.1 - For Exercises 21-36, simplify the expression....Ch. 5.1 - For Exercises 21-36, simplify the expression....Ch. 5.1 - For Exercises 21-36, simplify the expression....Ch. 5.1 - For Exercises 21-36, simplify the expression....Ch. 5.1 - For Exercises 21-36, simplify the expression....Ch. 5.1 - For Exercises 21-36, simplify the expression....Ch. 5.1 - For Exercises 21-36, simplify the expression....Ch. 5.1 - For Exercises 37-40, verify that the equation is...Ch. 5.1 - For Exercises 37-40, verify that the equation is...Ch. 5.1 - For Exercises 37-40, verify that the equation is...Ch. 5.1 - For Exercises 37-40, verify that the equation is...Ch. 5.1 - For Exercises 41-46, verify that the equation is...Ch. 5.1 - For Exercises 41-46, verify that the equation is...Ch. 5.1 - For Exercises 41-46, verify that the equation is...Ch. 5.1 - For Exercises 41-46, verify that the equation is...Ch. 5.1 - For Exercises 41-46, verify that the equation is...Ch. 5.1 - For Exercises 47-52, verify that the equation is...Ch. 5.1 - For Exercises 47-52, verify that the equation is...Ch. 5.1 - For Exercises 47-52, verify that the equation is...Ch. 5.1 - For Exercises 47-52, verify that the equation is...Ch. 5.1 - For Exercises 47-52, verify that the equation is...Ch. 5.1 - For Exercises 47-52, verify that the equation is...Ch. 5.1 - For Exercises 47-52, verify that the equation is...Ch. 5.1 - For Exercises 53-56, verify that the equation is...Ch. 5.1 - For Exercises 53-56, verify that the equation is...Ch. 5.1 - For Exercises 53-56, verify that the equation is...Ch. 5.1 - For Exercises 53-56, verify that the equation is...Ch. 5.1 - For Exercises 57-60, simplify each side of the...Ch. 5.1 - For Exercises 57-60, simplify each side of the...Ch. 5.1 - For Exercises 57-60, simplify each side of the...Ch. 5.1 - For Exercises 57-60, simplify each side of the...Ch. 5.1 - For Exercises 61-68, write the given algebraic...Ch. 5.1 - For Exercises 61-68, write the given algebraic...Ch. 5.1 - For Exercises 61-68, write the given algebraic...Ch. 5.1 - For Exercises 61-68, write the given algebraic...Ch. 5.1 - For Exercises 61-68, write the given algebraic...Ch. 5.1 - For Exercises 61-68, write the given algebraic...Ch. 5.1 - For Exercises 61-68, write the given algebraic...Ch. 5.1 - Prob. 68PECh. 5.1 - Prob. 69PECh. 5.1 - Prob. 70PECh. 5.1 - Prob. 71PECh. 5.1 - Prob. 72PECh. 5.1 - Prob. 73PECh. 5.1 - For Exercises 73-104, verify that the equation is...Ch. 5.1 - For Exercises 73-104, verify that the equation is...Ch. 5.1 - For Exercises 73-104, verify that the equation is...Ch. 5.1 - For Exercises 73-104, verify that the equation is...Ch. 5.1 - For Exercises 73-104, verify that the equation is...Ch. 5.1 - Prob. 79PECh. 5.1 - For Exercises 73-104, verify that the equation is...Ch. 5.1 - Prob. 81PECh. 5.1 - For Exercises 73-104, verify that the equation is...Ch. 5.1 - Prob. 83PECh. 5.1 - For Exercises 73-104, verify that the equation is...Ch. 5.1 - Prob. 85PECh. 5.1 - Prob. 86PECh. 5.1 - Prob. 87PECh. 5.1 - For Exercises 73-104, verify that the equation is...Ch. 5.1 - Prob. 89PECh. 5.1 - Prob. 90PECh. 5.1 - Prob. 91PECh. 5.1 - Prob. 92PECh. 5.1 - Prob. 93PECh. 5.1 - Prob. 94PECh. 5.1 - Prob. 95PECh. 5.1 - Prob. 96PECh. 5.1 - For Exercises 73-104, verify that the equation is...Ch. 5.1 - Prob. 98PECh. 5.1 - Prob. 99PECh. 5.1 - Prob. 100PECh. 5.1 - Prob. 101PECh. 5.1 - For Exercises 73-104, verify that the equation is...Ch. 5.1 - Prob. 103PECh. 5.1 - Prob. 104PECh. 5.1 - Prob. 105PECh. 5.1 - Prob. 106PECh. 5.1 - Prob. 107PECh. 5.1 - Prob. 108PECh. 5.1 - Prob. 109PECh. 5.1 - Prob. 110PECh. 5.1 - Prob. 111PECh. 5.1 - Prob. 112PECh. 5.1 - Prob. 113PECh. 5.1 - Prob. 114PECh. 5.1 - Prob. 115PECh. 5.1 - Prob. 116PECh. 5.1 - Prob. 117PECh. 5.1 - Prob. 118PECh. 5.2 - Find the exact values. a. sin195 b. cos512Ch. 5.2 - Find the exact value of the expression....Ch. 5.2 - Prob. 3SPCh. 5.2 - Prob. 4SPCh. 5.2 - Find the exact value of tan165 .Ch. 5.2 - Verify the identity. cos32=sinCh. 5.2 - Verify the identity. sinx+ysinxy=2cosxsinyCh. 5.2 - Write 4sinx+3cosx in the form ksinx+ .Ch. 5.2 - Prob. 1PECh. 5.2 - Prob. 2PECh. 5.2 - Fill in the boxes to complete each identity....Ch. 5.2 - Prob. 4PECh. 5.2 - Prob. 5PECh. 5.2 - Prob. 6PECh. 5.2 - For Exercises 7-18, use an addition or subtraction...Ch. 5.2 - For Exercises 7-18, use an addition or subtraction...Ch. 5.2 - For Exercises 7-18, use an addition or subtraction...Ch. 5.2 - For Exercises 7-18, use an addition or subtraction...Ch. 5.2 - For Exercises 7-18, use an addition or subtraction...Ch. 5.2 - For Exercises 7-18, use an addition or subtraction...Ch. 5.2 - For Exercises 7-18, use an addition or subtraction...Ch. 5.2 - For Exercises 7-18, use an addition or subtraction...Ch. 5.2 - For Exercises 7-18, use an addition or subtraction...Ch. 5.2 - For Exercises 7-18, use an addition or subtraction...Ch. 5.2 - For Exercises 7-18, use an addition or subtraction...Ch. 5.2 - For Exercises 7-18, use an addition or subtraction...Ch. 5.2 - For Exercises 19-26, use an addition or...Ch. 5.2 - For Exercises 19-26, use an addition or...Ch. 5.2 - For Exercises 19-26, use an addition or...Ch. 5.2 - For Exercises 19-26, use an addition or...Ch. 5.2 - For Exercises 19-26, use an addition or...Ch. 5.2 - For Exercises 19-26, use an addition or...Ch. 5.2 - For Exercises 19-26, use an addition or...Ch. 5.2 - For Exercises 19-26, use an addition or...Ch. 5.2 - For Exercises 27-32, find the exact value for the...Ch. 5.2 - For Exercises 27-32, find the exact value for the...Ch. 5.2 - For Exercises 27-32, find the exact value for the...Ch. 5.2 - Prob. 30PECh. 5.2 - Prob. 31PECh. 5.2 - Prob. 32PECh. 5.2 - Prob. 33PECh. 5.2 - Prob. 34PECh. 5.2 - Prob. 35PECh. 5.2 - Prob. 36PECh. 5.2 - Prob. 37PECh. 5.2 - For Exercises 33-40, find the exact value....Ch. 5.2 - Prob. 39PECh. 5.2 - Prob. 40PECh. 5.2 - Prob. 41PECh. 5.2 - Prob. 42PECh. 5.2 - Prob. 43PECh. 5.2 - For Exercises 41-62, verify the identity....Ch. 5.2 - Prob. 45PECh. 5.2 - Prob. 46PECh. 5.2 - Prob. 47PECh. 5.2 - For Exercises 41-62, verify the identity....Ch. 5.2 - Prob. 49PECh. 5.2 - Prob. 50PECh. 5.2 - Prob. 51PECh. 5.2 - For Exercises 41-62, verify the identity....Ch. 5.2 - Prob. 53PECh. 5.2 - Prob. 54PECh. 5.2 - Prob. 55PECh. 5.2 - For Exercises 41-62, verify the identity....Ch. 5.2 - Prob. 57PECh. 5.2 - Prob. 58PECh. 5.2 - Prob. 59PECh. 5.2 - Prob. 60PECh. 5.2 - Prob. 61PECh. 5.2 - Prob. 62PECh. 5.2 - Prob. 63PECh. 5.2 - For Exercises 63-66, a. Write the given expression...Ch. 5.2 - Prob. 65PECh. 5.2 - Prob. 66PECh. 5.2 - Prob. 67PECh. 5.2 - Prob. 68PECh. 5.2 - Prob. 69PECh. 5.2 - Prob. 70PECh. 5.2 - Prob. 71PECh. 5.2 - a. Is it true that cos245=2cos45 ? b. Expand...Ch. 5.2 - Derive cosu+v=cosucosvsinusinv by using the...Ch. 5.2 - Derive tanuv=tanutanv1+tanutanv by using the...Ch. 5.2 - Derive sinu+v=sinucosv+cosusinvCh. 5.2 - Prob. 76PECh. 5.2 - For fx=sinx , show that...Ch. 5.2 - Forfx=cosx , show that fx+hfxh=cosx1coshhsinxsinhhCh. 5.2 - Prob. 79PECh. 5.2 - Prob. 80PECh. 5.2 - Prob. 81PECh. 5.2 - Prob. 82PECh. 5.2 - Prob. 83PECh. 5.2 - Describe the pattern for the expansions of cosu+v...Ch. 5.2 - Prob. 85PECh. 5.2 - Prob. 86PECh. 5.2 - Prob. 87PECh. 5.2 - Prob. 88PECh. 5.2 - Prob. 89PECh. 5.2 - Prob. 90PECh. 5.2 - Prob. 91PECh. 5.2 - Prob. 92PECh. 5.2 - Prob. 93PECh. 5.2 - Prob. 94PECh. 5.2 - Prob. 95PECh. 5.2 - Prob. 96PECh. 5.2 - Prob. 97PECh. 5.2 - Suppose that ABC contains no right angle. Show...Ch. 5.2 - Let L be a line defined by y=mx+b with a positive...Ch. 5.2 - Prob. 100PECh. 5.2 - Prob. 101PECh. 5.2 - Prob. 102PECh. 5.3 - Given that sin=45 for in Quadrant II, find the...Ch. 5.3 - Prob. 2SPCh. 5.3 - Prob. 3SPCh. 5.3 - Use the half-angle formula to find the exact value...Ch. 5.3 - Show that 1cos1+cos=sin1+cos.Ch. 5.3 - Prob. 6SPCh. 5.3 - Prob. 1PECh. 5.3 - Prob. 2PECh. 5.3 - Prob. 3PECh. 5.3 - Prob. 4PECh. 5.3 - From the relationship sin2=1cos22, it follows that...Ch. 5.3 - From the relationship cos2=1+cos22 , it follows...Ch. 5.3 - For Exercises 7-14, use the given information to...Ch. 5.3 - For Exercises 7-14, use the given information to...Ch. 5.3 - For Exercises 7-14, use the given information to...Ch. 5.3 - For Exercises 7-14, use the given information to...Ch. 5.3 - For Exercises 7-14, use the given information to...Ch. 5.3 - For Exercises 7-14, use the given information to...Ch. 5.3 - For Exercises 7-14, use the given information to...Ch. 5.3 - For Exercises 7-14, use the given information to...Ch. 5.3 - For Exercises, 15-20, find the exact value of the...Ch. 5.3 - For Exercises, 15-20, find the exact value of the...Ch. 5.3 - For Exercises, 15-20, find the exact value of the...Ch. 5.3 - For Exercises, 15-20, find the exact value of the...Ch. 5.3 - For Exercises, 15-20, find the exact value of the...Ch. 5.3 - For Exercises, 15-20, find the exact value of the...Ch. 5.3 - Prob. 21PECh. 5.3 - Prob. 22PECh. 5.3 - Prob. 23PECh. 5.3 - Prob. 24PECh. 5.3 - Prob. 25PECh. 5.3 - For Exercises, 21-34, verify the identity....Ch. 5.3 - Prob. 27PECh. 5.3 - Prob. 28PECh. 5.3 - Prob. 29PECh. 5.3 - Prob. 30PECh. 5.3 - For Exercises, 21-34, verify the identity....Ch. 5.3 - Prob. 32PECh. 5.3 - For Exercises, 21-34, verify the identity....Ch. 5.3 - Prob. 34PECh. 5.3 - Prob. 35PECh. 5.3 - Prob. 36PECh. 5.3 - Prob. 37PECh. 5.3 - For Exercises 39-44, use the half-angle formula to...Ch. 5.3 - For Exercises 39-44, use the half-angle formula to...Ch. 5.3 - For Exercises 39-44, use the half-angle formula to...Ch. 5.3 - For Exercises 39-44, use the half-angle formula to...Ch. 5.3 - For Exercises 39-44, use the half-angle formula to...Ch. 5.3 - For Exercises 39-44, use the half-angle formula to...Ch. 5.3 - For Exercises 39-44, use the half-angle formula to...Ch. 5.3 - Fill the table for in the given quadrant, what do...Ch. 5.3 - What are the advantages to using the formula...Ch. 5.3 - For Exercises 47-50, use the given information to...Ch. 5.3 - For Exercises 47-50, use the given information to...Ch. 5.3 - For Exercises 47-50, use the given information to...Ch. 5.3 - For Exercises 47-50, use the given information to...Ch. 5.3 - For Exercises 51-56, verify the identity....Ch. 5.3 - Prob. 52PECh. 5.3 - Prob. 53PECh. 5.3 - Prob. 54PECh. 5.3 - Prob. 55PECh. 5.3 - Prob. 56PECh. 5.3 - Prob. 57PECh. 5.3 - Prob. 58PECh. 5.3 - Prob. 59PECh. 5.3 - Prob. 60PECh. 5.3 - Prob. 61PECh. 5.3 - Prob. 62PECh. 5.3 - Prob. 63PECh. 5.3 - Prob. 64PECh. 5.3 - Prob. 65PECh. 5.3 - Prob. 66PECh. 5.3 - Prob. 67PECh. 5.3 - Prob. 68PECh. 5.3 - Prob. 69PECh. 5.3 - Prob. 70PECh. 5.3 - For Exercises 71-74, a. Rewrite the function as a...Ch. 5.3 - Prob. 72PECh. 5.3 - For Exercises 71-74, a. Rewrite the function as a...Ch. 5.3 - For Exercises 71-74, a. Rewrite the function as a...Ch. 5.3 - Prob. 75PECh. 5.3 - For Exercises 75-80, find the exact value....Ch. 5.3 - Prob. 77PECh. 5.3 - Prob. 78PECh. 5.3 - Prob. 79PECh. 5.3 - For Exercises 75-80, find the exact value....Ch. 5.3 - Prob. 81PECh. 5.3 - Find an algebraic expression representing...Ch. 5.3 - A feeding trough for cattle is made from a metal...Ch. 5.3 - Consider the triangular area of the roof truss. a....Ch. 5.3 - Consider an object launched from an initial height...Ch. 5.3 - Refer to Exercise 85. Suppose that you kick a...Ch. 5.3 - Write cos3x as a third-degree polynomial in cosx .Ch. 5.3 - Write cos4x as a fourth-degree polynomial incosx .Ch. 5.3 - Prob. 89PECh. 5.3 - Prob. 90PECh. 5.3 - Prob. 91PECh. 5.3 - Prob. 92PECh. 5.3 - Prob. 93PECh. 5.3 - Prob. 94PECh. 5.3 - Prob. 95PECh. 5.3 - Prob. 96PECh. 5.3 - Prob. 97PECh. 5.3 - Prob. 98PECh. 5.3 - Prob. 99PECh. 5.3 - Prob. 100PECh. 5.4 - Write the product as a sum or difference. a....Ch. 5.4 - Use a product-to-sum formula to find the exact...Ch. 5.4 - Prob. 3SPCh. 5.4 - Use a sum-to-product formula to find the exact...Ch. 5.4 - Prob. 5SPCh. 5.4 - Prob. 1PECh. 5.4 - Prob. 2PECh. 5.4 - Prob. 3PECh. 5.4 - For Exercises 3-10, write the product as a sum or...Ch. 5.4 - For Exercises 3-10, write the product as a sum or...Ch. 5.4 - For Exercises 3-10, write the product as a sum or...Ch. 5.4 - For Exercises 3-10, write the product as a sum or...Ch. 5.4 - For Exercises 3-10, write the product as a sum or...Ch. 5.4 - Prob. 9PECh. 5.4 - Prob. 10PECh. 5.4 - Prob. 11PECh. 5.4 - In Exercises 11-14, use a product-to-sum formula...Ch. 5.4 - In Exercises 11-14, use a product-to-sum formula...Ch. 5.4 - In Exercises 11-14, use a product-to-sum formula...Ch. 5.4 - Prob. 15PECh. 5.4 - For Exercises 15-18, verify the identities....Ch. 5.4 - For Exercises 15-18, verify the identities....Ch. 5.4 - For Exercises 15-18, verify the identities....Ch. 5.4 - Prob. 19PECh. 5.4 - For Exercises 19-22, write each expression as a...Ch. 5.4 - Prob. 21PECh. 5.4 - For Exercises 19-22, write each expression as a...Ch. 5.4 - Prob. 23PECh. 5.4 - Prob. 24PECh. 5.4 - Prob. 25PECh. 5.4 - For Exercises 23-26, use a sum-to-product formula...Ch. 5.4 - For Exercises 27-34, verify the identity....Ch. 5.4 - For Exercises 27-34, verify the identity....Ch. 5.4 - Prob. 29PECh. 5.4 - Prob. 30PECh. 5.4 - Prob. 31PECh. 5.4 - Prob. 32PECh. 5.4 - Prob. 33PECh. 5.4 - Prob. 34PECh. 5.4 - Prob. 35PECh. 5.4 - Prob. 36PECh. 5.4 - Prob. 37PECh. 5.4 - Derive formula (3) on page 601....Ch. 5.4 - Derive formula (6) on page 602....Ch. 5.4 - Prob. 40PECh. 5.4 - Prob. 41PECh. 5.4 - Prob. 42PECh. 5.4 - Prob. 43PECh. 5.4 - Prob. 44PECh. 5.4 - Prob. 45PECh. 5.4 - Prob. 46PECh. 5.4 - Prob. 47PECh. 5.4 - Prob. 48PECh. 5.4 - In this section, we used the product-to-sum...Ch. 5.4 - In this section, we used the product-to-sum...Ch. 5.4 - Prob. 51PECh. 5.5 - Solvesinx=2sinx a. Over 0,2 . b. Over the set of...Ch. 5.5 - Solve the equation 1+cos3x=0 . a. Write the...Ch. 5.5 - Solve the equation 1+2cos2=0 . a. Write the...Ch. 5.5 - Solve the equation cotx4=1 . a. Write the solution...Ch. 5.5 - Solve the equation on the interval 0,2 ....Ch. 5.5 - Solve the equation on the interval 0,2 . 4cos2x3=0Ch. 5.5 - Solve the equation on the interval 0,2 ....Ch. 5.5 - Solve the equation on the interval 0,2 ....Ch. 5.5 - Solve the equation on the interval 0,2 ....Ch. 5.5 - Solve the equation on the interval 0,2 ....Ch. 5.5 - Solve the equation on the interval 0,2 . Give the...Ch. 5.5 - Use a graphing utility to solve the equation...Ch. 5.5 - How many solutions to the equation cosx=32 exist?...Ch. 5.5 - Prob. 2PECh. 5.5 - Prob. 3PECh. 5.5 - Given the equation sinx=0.2, one solution is...Ch. 5.5 - For Exercises 5-8, determine if the given value is...Ch. 5.5 - Prob. 6PECh. 5.5 - For Exercises 5-8, determine if the given value is...Ch. 5.5 - Prob. 8PECh. 5.5 - Prob. 9PECh. 5.5 - For Exercises 9-12, solve the equation over the...Ch. 5.5 - For Exercises 9-12, solve the equation over the...Ch. 5.5 - Prob. 12PECh. 5.5 - For Exercises 13-18, solve the equation a. Over...Ch. 5.5 - For Exercises 13-18, solve the equation a. Over...Ch. 5.5 - For Exercises 13-18, solve the equation a. Over...Ch. 5.5 - For Exercises 13-18, solve the equation a. Over...Ch. 5.5 - For Exercises 13-18, solve the equation a. Over...Ch. 5.5 - For Exercises 13-18, solve the equation a. Over...Ch. 5.5 - For Exercises 19-20, identify the number of...Ch. 5.5 - Prob. 20PECh. 5.5 - Prob. 21PECh. 5.5 - Prob. 22PECh. 5.5 - For Exercises 23-32, solve the equation. a. Write...Ch. 5.5 - For Exercises 23-32, solve the equation. a. Write...Ch. 5.5 - For Exercises 23-32, solve the equation. a. Write...Ch. 5.5 - Prob. 26PECh. 5.5 - For Exercises 23-32, solve the equation. a. Write...Ch. 5.5 - For Exercises 23-32, solve the equation. a. Write...Ch. 5.5 - Prob. 29PECh. 5.5 - For Exercises 23-32, solve the equation. a. Write...Ch. 5.5 - For Exercises 23-32, solve the equation. a. Write...Ch. 5.5 - For Exercises 23-32, solve the equation. a. Write...Ch. 5.5 - For Exercises 33-42, solve the equation on the...Ch. 5.5 - For Exercises 33-42, solve the equation on the...Ch. 5.5 - For Exercises 33-42, solve the equation on the...Ch. 5.5 - For Exercises 33-42, solve the equation on the...Ch. 5.5 - For Exercises 33-42, solve the equation on the...Ch. 5.5 - For Exercises 33-42, solve the equation on the...Ch. 5.5 - For Exercises 33-42, solve the equation on the...Ch. 5.5 - For Exercises 33-42, solve the equation on the...Ch. 5.5 - For Exercises 33-42, solve the equation on the...Ch. 5.5 - For Exercises 33-42, solve the equation on the...Ch. 5.5 - For Exercises 43-56, solve the equation on the...Ch. 5.5 - For Exercises 43-56, solve the equation on the...Ch. 5.5 - Prob. 45PECh. 5.5 - Prob. 46PECh. 5.5 - For Exercises 43-56, solve the equation on the...Ch. 5.5 - For Exercises 43-56, solve the equation on the...Ch. 5.5 - Prob. 49PECh. 5.5 - For Exercises 43-56, solve the equation on the...Ch. 5.5 - For Exercises 43-56, solve the equation on the...Ch. 5.5 - Prob. 52PECh. 5.5 - Prob. 53PECh. 5.5 - For Exercises 43-56, solve the equation on the...Ch. 5.5 - Prob. 55PECh. 5.5 - Prob. 56PECh. 5.5 - For Exercises 57-62, solve the equations on the...Ch. 5.5 - For Exercises 57-62, solve the equations on the...Ch. 5.5 - Prob. 59PECh. 5.5 - For Exercises 57-62, solve the equations on the...Ch. 5.5 - Prob. 61PECh. 5.5 - Prob. 62PECh. 5.5 - For Exercises 63-68, use a graphing utility to...Ch. 5.5 - For Exercises 63-68, use a graphing utility to...Ch. 5.5 - For Exercises 63-68, use a graphing utility to...Ch. 5.5 - Prob. 66PECh. 5.5 - For Exercises 63-68, use a graphing utility to...Ch. 5.5 - For Exercises 63-68, use a graphing utility to...Ch. 5.5 - For Exercises 69-88, solve the equation on the...Ch. 5.5 - Prob. 70PECh. 5.5 - For Exercises 69-88, solve the equation on the...Ch. 5.5 - Prob. 72PECh. 5.5 - For Exercises 69-88, solve the equation on the...Ch. 5.5 - For Exercises 69-88, solve the equation on the...Ch. 5.5 - For Exercises 69-88, solve the equation on the...Ch. 5.5 - For Exercises 69-88, solve the equation on the...Ch. 5.5 - Prob. 77PECh. 5.5 - Prob. 78PECh. 5.5 - For Exercises 69-88, solve the equation on the...Ch. 5.5 - For Exercises 69-88. solve the equation on the...Ch. 5.5 - For Exercises 69-88, solve the equation on the...Ch. 5.5 - For Exercises 69-88, solve the equation on the...Ch. 5.5 - For Exercises 69-88, solve the equation on the...Ch. 5.5 - For Exercises 69-88, solve the equation on the...Ch. 5.5 - Prob. 85PECh. 5.5 - Prob. 86PECh. 5.5 - For Exercises 69-88, solve the equation on the...Ch. 5.5 - For Exercises 69-88, solve the equation on the...Ch. 5.5 - The height ht (in feet) of the seat of a child's...Ch. 5.5 - A vertical spring is attached to the ceiling. The...Ch. 5.5 - The monthly sales of winter coats follow a...Ch. 5.5 - With each heartbeat, blood pressure increases as...Ch. 5.5 - The refractive index n of a substance is a...Ch. 5.5 - The refractive index n of a substance is a...Ch. 5.5 - Explain why cos2xcosx12=0 has no solution.Ch. 5.5 - Explain why x=sin10.4 is not a solution to the...Ch. 5.5 - What is the difference between the general...Ch. 5.5 - Explain two different methods to solve the...Ch. 5.5 - For Exercises 99-112, solve the equation on the...Ch. 5.5 - Prob. 100PECh. 5.5 - Prob. 101PECh. 5.5 - For Exercises 99-112, solve the equation on the...Ch. 5.5 - Prob. 103PECh. 5.5 - Prob. 104PECh. 5.5 - Prob. 105PECh. 5.5 - For Exercises 99-112, solve the equation on the...Ch. 5.5 - Prob. 107PECh. 5.5 - Prob. 108PECh. 5.5 - Prob. 109PECh. 5.5 - For Exercises 99-112, solve the equation on the...Ch. 5.5 - Prob. 111PECh. 5.5 - Prob. 112PECh. 5.5 - Consider the equation sinx+1=cosx from Example 10....Ch. 5.5 - For Exercises 114-116, use the technique from...Ch. 5.5 - Prob. 115PECh. 5.5 - Prob. 116PECh. 5.5 - Prob. 117PECh. 5.5 - From Exercise 83 in Section 5.3, the...Ch. 5.5 - Consider an isosceles triangle with two sides of...Ch. 5.5 - For Exercises 120-121, consider a projectile...Ch. 5.5 - For Exercises 120-121, consider a projectile...Ch. 5.5 - Suppose that a rectangle is bounded by the x-axis...Ch. 5.5 - For Exercises 1-6, prove the identity in part (a),...Ch. 5.5 - Prob. 2PRECh. 5.5 - Prob. 3PRECh. 5.5 - Prob. 4PRECh. 5.5 - Prob. 5PRECh. 5.5 - Prob. 6PRECh. 5.5 - Prob. 7PRECh. 5.5 - a. Compute cos12 by applying a sum or difference...Ch. 5 - For Exercises 1-2, factor the expression...Ch. 5 - For Exercises 1-2, factor the expression...Ch. 5 - For Exercises 3-4, find the LCD of the...Ch. 5 - Prob. 4RECh. 5 - Prob. 5RECh. 5 - For Exercises 5-6, simplify the expression....Ch. 5 - Prob. 7RECh. 5 - Prob. 8RECh. 5 - For Exercises 7-14, verify the identity....Ch. 5 - Prob. 10RECh. 5 - For Exercises 7-14, verify the identity....Ch. 5 - For Exercises 7-14, verify the identity....Ch. 5 - Prob. 13RECh. 5 - Prob. 14RECh. 5 - Write 16x2 as a function of by making the...Ch. 5 - Prob. 16RECh. 5 - Prob. 17RECh. 5 - In Exercises 17-26, use an addition or subtraction...Ch. 5 - Prob. 19RECh. 5 - Prob. 20RECh. 5 - Prob. 21RECh. 5 - In Exercises 17-26, use an addition or subtraction...Ch. 5 - In Exercises 17-26, use an addition or subtraction...Ch. 5 - In Exercises 17-26, use an addition or subtraction...Ch. 5 - In Exercises 17-26, use an addition or subtraction...Ch. 5 - In Exercises 17-26, use an addition or subtraction...Ch. 5 - Prob. 27RECh. 5 - Find the exact value for cos given sin=2129 for ...Ch. 5 - For Exercises 29-32, verify the identity....Ch. 5 - For Exercises 29-32, verify the identity....Ch. 5 - Prob. 31RECh. 5 - For Exercises 29-32, verify the identity....Ch. 5 - Write 3sinxcosx in the form ksinx+ for 02 .Ch. 5 - Write 3cosx4sinx in the form ksinx+a for 02 ....Ch. 5 - For Exercises 35-38, verify the identity....Ch. 5 - Prob. 36RECh. 5 - For Exercises 35-38, verify the identity....Ch. 5 - Prob. 38RECh. 5 - Write 16cos4x in terms of first powers of cosine.Ch. 5 - Prob. 40RECh. 5 - For Exercises 41-44, use the given information to...Ch. 5 - For Exercises 41-44, use the given information to...Ch. 5 - Prob. 43RECh. 5 - Prob. 44RECh. 5 - Prob. 45RECh. 5 - For Exercises 45-46, use the given information to...Ch. 5 - Prob. 47RECh. 5 - Prob. 48RECh. 5 - For Exercises 47-50, write the product as a sum or...Ch. 5 - For Exercises 47-50, write the product as a sum or...Ch. 5 - Prob. 51RECh. 5 - For Exercises 51-54, write each expression as a...Ch. 5 - Prob. 53RECh. 5 - Prob. 54RECh. 5 - For Exercises 55-56, use a product-to-sum formula...Ch. 5 - For Exercises 55-56, use a product-to-sum formula...Ch. 5 - Prob. 57RECh. 5 - Prob. 58RECh. 5 - For Exercises 59-60, use the sum-to-product...Ch. 5 - Prob. 60RECh. 5 - For Exercises 61-62, verify the identity....Ch. 5 - For Exercises 61-62, verify the identity....Ch. 5 - Prob. 63RECh. 5 - For Exercises 63-70, a. Write the solution set for...Ch. 5 - For Exercises 63-70, a. Write the solution set for...Ch. 5 - Prob. 66RECh. 5 - Prob. 67RECh. 5 - For Exercises 63-70, a. Write the solution set for...Ch. 5 - For Exercises 63-70, a. Write the solution set for...Ch. 5 - For Exercises 63-70, a. Write the solution set for...Ch. 5 - Prob. 71RECh. 5 - For Exercises 71-88, solve the equations on the...Ch. 5 - Prob. 73RECh. 5 - For Exercises 71-88, solve the equations on the...Ch. 5 - Prob. 75RECh. 5 - For Exercises 71-88, solve the equations on the...Ch. 5 - Prob. 77RECh. 5 - For Exercises 71-88, solve the equations on the...Ch. 5 - For Exercises 71-88, solve the equations on the...Ch. 5 - For Exercises 71-88, solve the equations on the...Ch. 5 - For Exercises 71-88, solve the equations on the...Ch. 5 - Prob. 82RECh. 5 - Prob. 83RECh. 5 - For Exercises 71-88, solve the equations on the...Ch. 5 - Prob. 85RECh. 5 - Prob. 86RECh. 5 - For Exercises 71-88, solve the equations on the...Ch. 5 - Prob. 88RECh. 5 - Prob. 89RECh. 5 - Prob. 90RECh. 5 - Prob. 91RECh. 5 - Prob. 92RECh. 5 - Prob. 93RECh. 5 - For Exercises 1-2, simplify the expression....Ch. 5 - Prob. 2TCh. 5 - Prob. 3TCh. 5 - For Exercises 3-8, verify the identity....Ch. 5 - Prob. 5TCh. 5 - Prob. 6TCh. 5 - Prob. 7TCh. 5 - Prob. 8TCh. 5 - Prob. 9TCh. 5 - Write 8cosx15sinx in the form ksinx+ for 02 ....Ch. 5 - Prob. 11TCh. 5 - For Exercises 12-17, find the exact value....Ch. 5 - Prob. 13TCh. 5 - For Exercises 12-17, find the exact value....Ch. 5 - Prob. 15TCh. 5 - Prob. 16TCh. 5 - For Exercises 12-17, find the exact value....Ch. 5 - Prob. 18TCh. 5 - Prob. 19TCh. 5 - Given tan=158 and 32 find the exact function...Ch. 5 - For Exercises 21-22 a. Write the solution set for...Ch. 5 - Prob. 22TCh. 5 - For Exercises 23-30, solve the equation on the...Ch. 5 - For Exercises 23-30, solve the equation on the...Ch. 5 - For Exercises 23-30, solve the equation on the...Ch. 5 - Prob. 26TCh. 5 - Prob. 27TCh. 5 - Prob. 28TCh. 5 - Prob. 29TCh. 5 - For Exercises 23-30, solve the equation on the...Ch. 5 - Prob. 31TCh. 5 - For a projectile launched from ground level at an...Ch. 5 - Prob. 1CRECh. 5 - Prob. 2CRECh. 5 - Prob. 3CRECh. 5 - Prob. 4CRECh. 5 - Prob. 5CRECh. 5 - Prob. 6CRECh. 5 - Prob. 7CRECh. 5 - Prob. 8CRECh. 5 - Prob. 9CRECh. 5 - Prob. 10CRECh. 5 - Prob. 11CRECh. 5 - Prob. 12CRECh. 5 - Prob. 13CRECh. 5 - Prob. 14CRECh. 5 - Prob. 15CRECh. 5 - Prob. 16CRECh. 5 - Given fx=log3x, a. Write the domain and range in...Ch. 5 - Prob. 18CRECh. 5 - Prob. 19CRECh. 5 - Prob. 20CRE
Additional Math Textbook Solutions
Find more solutions based on key concepts
29-36. Total and Annual Returns. Compute the total and annual returns on the following investments.
29. Five ye...
Using and Understanding Mathematics: A Quantitative Reasoning Approach (6th Edition)
Heights Refer to the dotplot in the previous question. a. What is the height of a woman with a z-score of -1? b...
Introductory Statistics
Identify f as being linear, quadratic, or neither. If f is quadratic, identify the leading coefficient a and ...
College Algebra with Modeling & Visualization (5th Edition)
Fill in each blank so that the resulting statement is true. Any set of ordered pairs is called a/an ____.The se...
Algebra and Trigonometry (6th Edition)
The missing measure x in two similar triangles given.
Pre-Algebra Student Edition
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Provethat a) prove that for any irrational numbers there exists? asequence of rational numbers Xn converg to S. b) let S: RR be a sunctions-t. f(x)=(x-1) arc tan (x), xe Q 3(x-1) 1+x² x&Q Show that lim f(x)= 0 14x C) For any set A define the set -A=yarrow_forwardQ2: Find the interval and radius of convergence for the following series: Σ n=1 (-1)η-1 xn narrow_forward8. Evaluate arctan x dx a) xartanx 2 2 In(1 + x²) + C b) xartanx + 1½-3ln(1 + x²) + C c) xartanx + In(1 + x²) + C d) (arctanx)² + C 2 9) Evaluate Inx³ dx 3 a) +C b) ln x² + C c)¾½ (lnx)² d) 3x(lnx − 1) + C - x 10) Determine which integral is obtained when the substitution x = So¹² √1 - x²dx sine is made in the integral πT π π a) √ sin cos e de b) √ cos² de c) c Ꮎ Ꮎ cos² 0 de c) cos e de d) for cos² e de πT 11. Evaluate tan³xdx 1 a) b) c) [1 - In 2] 2 2 c) [1 − In2] d)½½[1+ In 2]arrow_forward
- 12. Evaluate ſ √9-x2 -dx. x2 a) C 9-x2 √9-x2 - x2 b) C - x x arcsin ½-½ c) C + √9 - x² + arcsin x d) C + √9-x2 x2 13. Find the indefinite integral S cos³30 √sin 30 dᎾ . 2√√sin 30 (5+sin²30) √sin 30 (3+sin²30) a) C+ √sin 30(5-sin²30) b) C + c) C + 5 5 5 10 d) C + 2√√sin 30 (3-sin²30) 2√√sin 30 (5-sin²30) e) C + 5 15 14. Find the indefinite integral ( sin³ 4xcos 44xdx. a) C+ (7-5cos24x)cos54x b) C (7-5cos24x)cos54x (7-5cos24x)cos54x - 140 c) C - 120 140 d) C+ (7-5cos24x)cos54x e) C (7-5cos24x)cos54x 4 4 15. Find the indefinite integral S 2x2 dx. ex - a) C+ (x²+2x+2)ex b) C (x² + 2x + 2)e-* d) C2(x²+2x+2)e¯* e) C + 2(x² + 2x + 2)e¯* - c) C2x(x²+2x+2)e¯*arrow_forward4. Which substitution would you use to simplify the following integrand? S a) x = sin b) x = 2 tan 0 c) x = 2 sec 3√√3 3 x3 5. After making the substitution x = = tan 0, the definite integral 2 2 3 a) ៖ ស្លឺ sin s π - dᎾ 16 0 cos20 b) 2/4 10 cos 20 π sin30 6 - dᎾ c) Π 1 cos³0 3 · de 16 0 sin20 1 x²√x²+4 3 (4x²+9)2 π d) cos²8 16 0 sin³0 dx d) x = tan 0 dx simplifies to: de 6. In order to evaluate (tan 5xsec7xdx, which would be the most appropriate strategy? a) Separate a sec²x factor b) Separate a tan²x factor c) Separate a tan xsecx factor 7. Evaluate 3x x+4 - dx 1 a) 3x+41nx + 4 + C b) 31n|x + 4 + C c) 3 ln x + 4+ C d) 3x - 12 In|x + 4| + C x+4arrow_forward1. Abel's Theorem. The goal in this problem is to prove Abel's theorem by following a series of steps (each step must be justified). Theorem 0.1 (Abel's Theorem). If y1 and y2 are solutions of the differential equation y" + p(t) y′ + q(t) y = 0, where p and q are continuous on an open interval, then the Wronskian is given by W (¥1, v2)(t) = c exp(− [p(t) dt), where C is a constant that does not depend on t. Moreover, either W (y1, y2)(t) = 0 for every t in I or W (y1, y2)(t) = 0 for every t in I. 1. (a) From the two equations (which follow from the hypotheses), show that y" + p(t) y₁ + q(t) y₁ = 0 and y½ + p(t) y2 + q(t) y2 = 0, 2. (b) Observe that Hence, conclude that (YY2 - Y1 y2) + P(t) (y₁ Y2 - Y1 Y2) = 0. W'(y1, y2)(t) = yY2 - Y1 y2- W' + p(t) W = 0. 3. (c) Use the result from the previous step to complete the proof of the theorem.arrow_forward
- 2. Observations on the Wronskian. Suppose the functions y₁ and y2 are solutions to the differential equation p(x)y" + q(x)y' + r(x) y = 0 on an open interval I. 1. (a) Prove that if y₁ and y2 both vanish at the same point in I, then y₁ and y2 cannot form a fundamental set of solutions. 2. (b) Prove that if y₁ and y2 both attain a maximum or minimum at the same point in I, then y₁ and Y2 cannot form a fundamental set of solutions. 3. (c) show that the functions & and t² are linearly independent on the interval (−1, 1). Verify that both are solutions to the differential equation t² y″ – 2ty' + 2y = 0. Then justify why this does not contradict Abel's theorem. 4. (d) What can you conclude about the possibility that t and t² are solutions to the differential equation y" + q(x) y′ + r(x)y = 0?arrow_forwardQuestion 4 Find an equation of (a) The plane through the point (2, 0, 1) and perpendicular to the line x = y=2-t, z=3+4t. 3t, (b) The plane through the point (3, −2, 8) and parallel to the plane z = x+y. (c) The plane that contains the line x = 1+t, y = 2 − t, z = 4 - 3t and is parallel to the plane 5x + 2y + z = 1. (d) The plane that passes through the point (1,2,3) and contains the line x = 3t, y = 1+t, and z = 2-t. (e) The plane that contains the lines L₁: x = 1 + t, y = 1 − t, z = 2t and L2 : x = 2 − s, y = s, z = 2.arrow_forwardPlease find all values of x.arrow_forward
- 3. Consider the initial value problem 9y" +12y' + 4y = 0, y(0) = a>0: y′(0) = −1. Solve the problem and find the value of a such that the solution of the initial value problem is always positive.arrow_forward5. Euler's equation. Determine the values of a for which all solutions of the equation 5 x²y" + axy' + y = 0 that have the form (A + B log x) x* or Ax¹¹ + Bä” tend to zero as a approaches 0.arrow_forward4. Problem on variable change. The purpose of this problem is to perform an appropriate change of variables in order to reduce the problem to a second-order equation with constant coefficients. ty" + (t² − 1)y'′ + t³y = 0, 0arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning  Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage

Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning

Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning

Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Fundamental Trigonometric Identities: Reciprocal, Quotient, and Pythagorean Identities; Author: Mathispower4u;https://www.youtube.com/watch?v=OmJ5fxyXrfg;License: Standard YouTube License, CC-BY