Chapter 5.2, Problem 4CYU

To determine

Solve for the unknown variable from the inequality equation.

Answer to Problem 4CYU

  $c\le -42$

Explanation of Solution

Given:

The inequality equation: $-\frac{c}{6}\ge 7$

Concept Used:

In mathematics, an inequality is a relation which makes a non-equal comparison between two numbers or other mathematical expressions. It is used most often to compare two numbers on the number line by their size.

An inequality compares two values, showing if one is less than, greater than, or simply not equal to another value. a ≠ b says that a is not equal to b. a < b says that a is less than b. a > b says that a is greater than b.

There are four different types of inequalities:

Greater than − $(>)$ ; Less than − $(<)$ ; Greater than or equal to − $(\ge )$ ; Less than or equal to − $(\le )$

For Inequality equation: If $b>c\Rightarrow c<b\text{or}b<c\Rightarrow c>b$

Rules for solving inequality equations:

These things do not affect the direction of the inequality:

• Add (or subtract) a number from both sides
• Multiply (or divide) both sides by a positive number
• Simplify a side

But these things do change the direction of the inequality (" $<$ " becomes " $>$ " for example):

• Multiply (or divide) both sides by a negative number
• Swapping left and right hand sides

Calculation:

The inequality equation: $-\frac{c}{6}\ge 7$

Solve:

  $\begin{array}{l}-\frac{c}{6}\ge 7\\ -6·\frac{c}{6}\le -6·7[[\text{Multiply}\text{both}\text{sides}\text{by}-6\text{and}\text{reverse}\text{the}\text{inequality}\text{]}\\ c\le -42\end{array}$

Solution of the inequality equation is $c\le -42$

Solution set: $(-\infty ,-42]$

A closed, or shaded, circle is used to represent the inequalities greater than or equal to ( $\ge$ ) or less than or equal to ( $\le$ ). The point is part of the solution.

Solution set on the number line

  

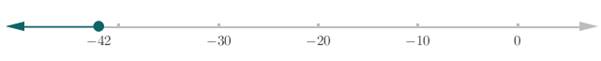
Thus, the solution of the inequality equation $-\frac{c}{6}\ge 7$ is $c\le -42$