
Calculus: Early Transcendentals (3rd Edition)
3rd Edition
ISBN: 9780134763644
Author: William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 5.2, Problem 47E
Net area from graphs The accompanying figure shows four regions bounded by the graph of y = x sin x: R1, R2, R3, and R4, whose areas are 1, π − 1, π + 1, and 2π − 1, respectively. (We verify these results later in the text.) Use this information to evaluate the following integrals.
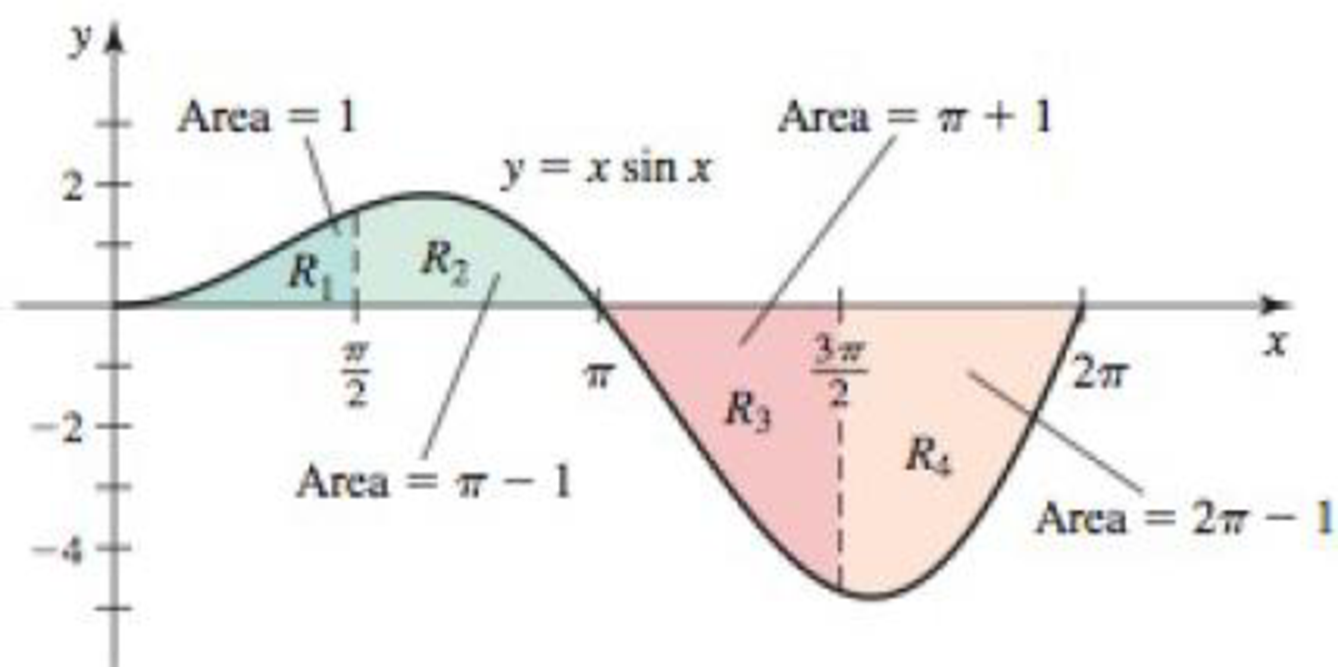
37. ∫π0xsinx dx
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
I forgot to mention to you to solve question 1 and 2. Can you solve it using all data that given in the pict i given and can you teach me about that.
exam review please help!
exam review please help!
Chapter 5 Solutions
Calculus: Early Transcendentals (3rd Edition)
Ch. 5.1 - What is the displacement of an object that travels...Ch. 5.1 - In Example 1, if we used n = 32 subintervals of...Ch. 5.1 - If the interval [1, 9] is partitioned into 4...Ch. 5.1 - If the function in Example 2 is replaced with f(x)...Ch. 5.1 - Suppose an object moves along a line at 15 m/s,...Ch. 5.1 - Given the graph of the positive velocity of an...Ch. 5.1 - Prob. 3ECh. 5.1 - The velocity in ft/s or an object moving along a...Ch. 5.1 - The velocity in ft/s of an object moving along a...Ch. 5.1 - The velocity in ft/s of an object moving along a...
Ch. 5.1 - Prob. 7ECh. 5.1 - Explain how Riemann sum approximations to the area...Ch. 5.1 - Prob. 9ECh. 5.1 - Prob. 10ECh. 5.1 - Suppose the interval [1, 3] is partitioned into n...Ch. 5.1 - Prob. 12ECh. 5.1 - Does a right Riemann sum underestimate or...Ch. 5.1 - Does a left Riemann sum underestimate or...Ch. 5.1 - Approximating displacement The velocity in ft/s of...Ch. 5.1 - Approximating displacement The velocity in ft/s of...Ch. 5.1 - Approximating displacement The velocity of an...Ch. 5.1 - Approximating displacement The velocity of an...Ch. 5.1 - Approximating displacement The velocity of an...Ch. 5.1 - Approximating displacement The velocity of an...Ch. 5.1 - Approximating displacement The velocity of an...Ch. 5.1 - Approximating displacement The velocity of an...Ch. 5.1 - Prob. 23ECh. 5.1 - Prob. 24ECh. 5.1 - Prob. 25ECh. 5.1 - Prob. 26ECh. 5.1 - Prob. 27ECh. 5.1 - Prob. 28ECh. 5.1 - Prob. 29ECh. 5.1 - Prob. 30ECh. 5.1 - Prob. 31ECh. 5.1 - Prob. 32ECh. 5.1 - A midpoint Riemann sum Approximate the area of the...Ch. 5.1 - Prob. 34ECh. 5.1 - Free fall On October 14, 2012, Felix Baumgartner...Ch. 5.1 - Free fall Use geometry and the figure given in...Ch. 5.1 - Prob. 37ECh. 5.1 - Midpoint Riemann sums Complete the following steps...Ch. 5.1 - Prob. 39ECh. 5.1 - Prob. 40ECh. 5.1 - Prob. 41ECh. 5.1 - Prob. 42ECh. 5.1 - Riemann sums from tables Evaluate the left and...Ch. 5.1 - Prob. 44ECh. 5.1 - Displacement from a table of velocities The...Ch. 5.1 - Displacement from a table of velocities The...Ch. 5.1 - Sigma notation Express the following sums using...Ch. 5.1 - Sigma notation Express the following sums using...Ch. 5.1 - Sigma notation Evaluate the following expressions....Ch. 5.1 - Evaluating sums Evaluate the following expressions...Ch. 5.1 - Prob. 51ECh. 5.1 - Prob. 52ECh. 5.1 - Prob. 53ECh. 5.1 - Prob. 54ECh. 5.1 - Prob. 55ECh. 5.1 - Prob. 56ECh. 5.1 - Prob. 57ECh. 5.1 - Prob. 58ECh. 5.1 - Explain why or why not Determine whether the...Ch. 5.1 - Prob. 60ECh. 5.1 - Prob. 61ECh. 5.1 - Prob. 62ECh. 5.1 - Prob. 63ECh. 5.1 - Prob. 64ECh. 5.1 - Identifying Riemann sums Fill in the blanks with...Ch. 5.1 - Identifying Riemann sums Fill in the blanks with...Ch. 5.1 - Prob. 67ECh. 5.1 - Prob. 68ECh. 5.1 - Approximating areas Estimate the area of the...Ch. 5.1 - Displacement from a velocity graph Consider the...Ch. 5.1 - Displacement from a velocity graph Consider the...Ch. 5.1 - Flow rates Suppose a gauge at the outflow of a...Ch. 5.1 - Mass from density A thin 10-cm rod is made of an...Ch. 5.1 - Prob. 74ECh. 5.1 - Prob. 75ECh. 5.1 - Prob. 76ECh. 5.1 - Prob. 77ECh. 5.1 - Riemann sums for constant functions Let f(x) = c,...Ch. 5.1 - Prob. 79ECh. 5.1 - Prob. 80ECh. 5.1 - Prob. 81ECh. 5.2 - Suppose f(x) = 5. What is the net area of the...Ch. 5.2 - Sketch a continuous function f that is positive...Ch. 5.2 - Graph f(x) = x and use geometry to evaluate 11xdx.Ch. 5.2 - Let f(x) = 5 and use geometry to evaluate...Ch. 5.2 - Evaluate abf(x)dx+baf(x)dx assuming f is integrate...Ch. 5.2 - Evaluate 12xdx and 12|x|dx using geometry.Ch. 5.2 - What does net area measure?Ch. 5.2 - Under what conditions does the net area of a...Ch. 5.2 - Prob. 3ECh. 5.2 - Use the graph of y = g(x) to estimate 210g(x)dx...Ch. 5.2 - Suppose f is continuous on [2, 8]. Use the table...Ch. 5.2 - Suppose g is continuous on [1, 9]. Use the table...Ch. 5.2 - Sketch a graph of y = 2 on [1, 4] and use geometry...Ch. 5.2 - Sketch a graph of y = 3 on [1, 5] and use geometry...Ch. 5.2 - Sketch a graph of y = 2x on [1, 2] and use...Ch. 5.2 - Suppose 13f(x)dx=10 and 13g(x)dx=20. Evaluate...Ch. 5.2 - Use graphs to evaluate 02sinxdx and 02cosxdx.Ch. 5.2 - Explain how the notation for Riemann sums,...Ch. 5.2 - Give a geometrical explanation of why aaf(x)dx=0.Ch. 5.2 - Use Table 5.4 to rewrite 16(2x34x)dx as the...Ch. 5.2 - Use geometry to find a formula for 0axdx, in terms...Ch. 5.2 - If f is continuous on [a, b] and abf(x)dx=0, what...Ch. 5.2 - Approximating net area The following functions are...Ch. 5.2 - Approximating net area The following functions are...Ch. 5.2 - Approximating net area The following functions are...Ch. 5.2 - Approximating net area The following functions are...Ch. 5.2 - Approximating net area The following functions are...Ch. 5.2 - Approximating net area The following functions are...Ch. 5.2 - Approximating net area The following functions are...Ch. 5.2 - Approximating net area The following functions are...Ch. 5.2 - Approximating net area The following functions are...Ch. 5.2 - Approximating net area The following functions are...Ch. 5.2 - Prob. 27ECh. 5.2 - Prob. 28ECh. 5.2 - Prob. 29ECh. 5.2 - Prob. 30ECh. 5.2 - Approximating definite integrals Complete the...Ch. 5.2 - Approximating definite integrals Complete the...Ch. 5.2 - Approximating definite integrals Complete the...Ch. 5.2 - Approximating definite integrals Complete the...Ch. 5.2 - Prob. 35ECh. 5.2 - Prob. 36ECh. 5.2 - Identifying definite integrals as limits of sums...Ch. 5.2 - Prob. 38ECh. 5.2 - Net area and definite integrals Use geometry (not...Ch. 5.2 - Net area and definite integrals Use geometry (not...Ch. 5.2 - Net area and definite integrals Use geometry (not...Ch. 5.2 - Net area and definite integrals Use geometry (not...Ch. 5.2 - Net area and definite integrals Use geometry (not...Ch. 5.2 - Net area and definite integrals Use geometry (not...Ch. 5.2 - Net area and definite integrals Use geometry (not...Ch. 5.2 - Net area and definite integrals Use geometry (not...Ch. 5.2 - Net area from graphs The accompanying figure shows...Ch. 5.2 - Net area from graphs The accompanying figure shows...Ch. 5.2 - Net area from graphs The accompanying figure shows...Ch. 5.2 - Net area from graphs The accompanying figure shows...Ch. 5.2 - Properties of integrals Use only the fact that...Ch. 5.2 - Properties of integrals Suppose 14f(x)dx=8 and...Ch. 5.2 - Properties of integrals Suppose 03f(x)dx=2,...Ch. 5.2 - Properties of integrals Suppose f(x) 0 on [0, 2],...Ch. 5.2 - More properties of integrals Consider two...Ch. 5.2 - Suppose f is continuous on [1, 5] and 2 f(x) 3...Ch. 5.2 - Using properties of integrals Use the value of the...Ch. 5.2 - Using properties of integrals Use the value of the...Ch. 5.2 - Net area from graphs The figure shows the areas of...Ch. 5.2 - Net area from graphs The figure shows the areas of...Ch. 5.2 - Net area from graphs The figure shows the areas of...Ch. 5.2 - Net area from graphs The figure shows the areas of...Ch. 5.2 - Definite integrals from graphs The figure shows...Ch. 5.2 - Definite integrals from graphs The figure shows...Ch. 5.2 - Definite integrals from graphs The figure shows...Ch. 5.2 - Definite integrals from graphs The figure shows...Ch. 5.2 - Use geometry and properties of integrals to...Ch. 5.2 - Use geometry and properties of integrals to...Ch. 5.2 - Explain why or why not Determine whether the...Ch. 5.2 - Approximating definite integrals with a calculator...Ch. 5.2 - Approximating definite integrals with a calculator...Ch. 5.2 - Approximating definite integrals with a calculator...Ch. 5.2 - Approximating definite integrals with a calculator...Ch. 5.2 - Approximating definite integrals with a calculator...Ch. 5.2 - Midpoint Riemann sums with a calculator Consider...Ch. 5.2 - Midpoint Riemann sums with a calculator Consider...Ch. 5.2 - Midpoint Riemann sums with a calculator Consider...Ch. 5.2 - Midpoint Riemann sums with a calculator Consider...Ch. 5.2 - Limits of sums Use the definition of the definite...Ch. 5.2 - Limits of sums Use the definition of the definite...Ch. 5.2 - Limits of sums Use the definition of the definite...Ch. 5.2 - Limits of sums Use the definition of the definite...Ch. 5.2 - Limits of sums Use the definition of the definite...Ch. 5.2 - Limits of sums Use the definition of the definite...Ch. 5.2 - Limits of sums Use the definition of the definite...Ch. 5.2 - Area by geometry Use geometry to evaluate the...Ch. 5.2 - Area by geometry Use geometry to evaluate the...Ch. 5.2 - Integrating piecewise continuous functions Suppose...Ch. 5.2 - Integrating piecewise continuous functions Use...Ch. 5.2 - Integrating piecewise continuous functions Use...Ch. 5.2 - Integrating piecewise continuous functions Recall...Ch. 5.2 - Integrating piecewise continuous functions Recall...Ch. 5.2 - Constants in integrals Use the definition of the...Ch. 5.2 - Zero net area If 0 c d, then find the value of b...Ch. 5.2 - A nonintegrable function Consider the function...Ch. 5.2 - Powers of x by Riemann sums Consider the integral...Ch. 5.2 - An exact integration formula Evaluate abdxx2,...Ch. 5.2 - Use Property 3 of Table 5.4 and Property 7 of...Ch. 5.3 - In Example 1, let B(x) be the area function for f...Ch. 5.3 - Verify that the area function in Example 2c gives...Ch. 5.3 - Evaluate (xx+1)|12.Ch. 5.3 - Explain why f is an antiderivative of f.Ch. 5.3 - Suppose A is an area function of f. What is the...Ch. 5.3 - Suppose F is an antiderivative of f and A is an...Ch. 5.3 - Explain in words and write mathematically how the...Ch. 5.3 - Let f(x) = c, where c is a positive constant....Ch. 5.3 - The linear function f(x) = 3 x is decreasing on...Ch. 5.3 - Evaluate 023x2dx and 223x2dx.Ch. 5.3 - Explain in words and express mathematically the...Ch. 5.3 - Why can the constant of integration be omitted...Ch. 5.3 - Evaluate ddxaxf(t)dt and ddxabf(t)dt, where a and...Ch. 5.3 - Explain why abf(x)dx=f(b)f(a).Ch. 5.3 - Evaluate 38f(t)dt, where f is continuous on [3,...Ch. 5.3 - Evaluate 273dx using the Fundamental Theorem of...Ch. 5.3 - Prob. 13ECh. 5.3 - Area functions The graph of f is shown in the...Ch. 5.3 - Area functions for constant functions Consider the...Ch. 5.3 - Area functions for constant functions Consider the...Ch. 5.3 - Area functions for the same linear function Let...Ch. 5.3 - Area functions for the same linear function Let...Ch. 5.3 - Area functions for linear functions Consider the...Ch. 5.3 - Area functions for linear functions Consider the...Ch. 5.3 - Area functions for linear functions Consider the...Ch. 5.3 - Area functions for linear functions Consider the...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following definite...Ch. 5.3 - Definite integrals Evaluate the following definite...Ch. 5.3 - Definite integrals Evaluate the following definite...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following definite...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following definite...Ch. 5.3 - Definite integrals Evaluate the following definite...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Areas Find (i) the net area and (ii) the area of...Ch. 5.3 - Areas Find (i) the net area and (ii) the area of...Ch. 5.3 - Areas Find (i) the net area and (ii) the area of...Ch. 5.3 - Areas Find (i) the net area and (ii) the area of...Ch. 5.3 - Areas of regions Find the area of the region...Ch. 5.3 - Areas of regions Find the area of the region...Ch. 5.3 - Areas of regions Find the area of the region...Ch. 5.3 - Areas of regions Find the area of the region...Ch. 5.3 - Areas of regions Find the area of the region...Ch. 5.3 - Areas of regions Find the area of the region...Ch. 5.3 - Derivatives of integrals Simplify the following...Ch. 5.3 - Derivatives and integrals Simplify the given...Ch. 5.3 - Derivatives of integrals Simplify the following...Ch. 5.3 - Derivatives of integrals Simplify the following...Ch. 5.3 - Derivatives of integrals Simplify the following...Ch. 5.3 - Derivatives and integrals Simplify the given...Ch. 5.3 - Derivatives and integrals Simplify the given...Ch. 5.3 - Derivatives of integrals Simplify the following...Ch. 5.3 - Derivatives of integrals Simplify the following...Ch. 5.3 - Derivatives of integrals Simplify the following...Ch. 5.3 - Derivatives and integrals Simplify the given...Ch. 5.3 - Derivatives and integrals Simplify the given...Ch. 5.3 - Derivatives of integrals Simplify the following...Ch. 5.3 - Derivatives of integrals Simplify the following...Ch. 5.3 - Prob. 87ECh. 5.3 - Working with area functions Consider the function...Ch. 5.3 - Prob. 89ECh. 5.3 - Prob. 90ECh. 5.3 - Prob. 91ECh. 5.3 - Prob. 92ECh. 5.3 - Area functions from graphs The graph of f is given...Ch. 5.3 - Prob. 94ECh. 5.3 - Working with area functions Consider the function...Ch. 5.3 - Working with area functions Consider the function...Ch. 5.3 - Prob. 97ECh. 5.3 - Prob. 98ECh. 5.3 - Find the critical points of the function...Ch. 5.3 - Determine the intervals on which the function...Ch. 5.3 - Prob. 101ECh. 5.3 - Prob. 102ECh. 5.3 - Areas of regions Find the area of the region R...Ch. 5.3 - Prob. 104ECh. 5.3 - Areas of regions Find the area of the region R...Ch. 5.3 - Areas of regions Find the area of the region R...Ch. 5.3 - Explain why or why not Determine whether the...Ch. 5.3 - Explorations and Challenges Evaluate...Ch. 5.3 - Maximum net area What value of b 1 maximizes the...Ch. 5.3 - Maximum net area Graph the function f(x) = 8 + 2x ...Ch. 5.3 - Prob. 111ECh. 5.3 - Cubic zero net area Consider the graph of the...Ch. 5.3 - An integral equation Use the Fundamental Theorem...Ch. 5.3 - Prob. 114ECh. 5.3 - Asymptote of sine integral Use a calculator to...Ch. 5.3 - Sine integral Show that the sine integral...Ch. 5.3 - Prob. 117ECh. 5.3 - Continuity at the endpoints Assume that f is...Ch. 5.3 - Discrete version of the Fundamental Theorem In...Ch. 5.4 - If f and g are both even functions, is the product...Ch. 5.4 - Prob. 2QCCh. 5.4 - Explain why f(x) = 0 for at least one point of (a,...Ch. 5.4 - If f is an odd function, why is aaf(x)dx=0?Ch. 5.4 - If f is an even function, why is...Ch. 5.4 - Using symmetry Suppose f is an even function and...Ch. 5.4 - Using symmetry Suppose f is an odd function,...Ch. 5.4 - Use symmetry to explain why...Ch. 5.4 - Use symmetry to fill in the blanks:...Ch. 5.4 - Is x12 an even or odd function? Is sin x2 an even...Ch. 5.4 - Prob. 8ECh. 5.4 - Prob. 9ECh. 5.4 - Prob. 10ECh. 5.4 - Symmetry in integrals Use symmetry to evaluate the...Ch. 5.4 - Symmetry in integrals Use symmetry to evaluate the...Ch. 5.4 - Symmetry in integrals Use symmetry to evaluate the...Ch. 5.4 - Symmetry in integrals Use symmetry to evaluate the...Ch. 5.4 - Symmetry in integrals Use symmetry to evaluate the...Ch. 5.4 - Symmetry in integrals Use symmetry to evaluate the...Ch. 5.4 - Symmetry in integrals Use symmetry to evaluate the...Ch. 5.4 - Symmetry in integrals Use symmetry to evaluate the...Ch. 5.4 - Symmetry in integrals Use symmetry to evaluate the...Ch. 5.4 - Symmetry in integrals Use symmetry to evaluate the...Ch. 5.4 - Symmetry in integrals Use symmetry to evaluate the...Ch. 5.4 - Symmetry in integrals Use symmetry to evaluate the...Ch. 5.4 - Symmetry in integrals Use symmetry to evaluate the...Ch. 5.4 - Symmetry in integrals Use symmetry to evaluate the...Ch. 5.4 - Average values Find the average value of the...Ch. 5.4 - Average values Find the average value of the...Ch. 5.4 - Average values Find the average value of the...Ch. 5.4 - Average values Find the average value of the...Ch. 5.4 - Average values Find the average value of the...Ch. 5.4 - Average values Find the average value of the...Ch. 5.4 - Average values Find the average value of the...Ch. 5.4 - Average values Find the average value of the...Ch. 5.4 - Average distance on a parabola What is the average...Ch. 5.4 - Average elevation The elevation of a path is given...Ch. 5.4 - Average velocity The velocity in m/s of an object...Ch. 5.4 - Average velocity A rock is launched vertically...Ch. 5.4 - Average height of an arch The height of an arch...Ch. 5.4 - Average height of a wave The surface of a water...Ch. 5.4 - Mean Value Theorem for Integrals Find or...Ch. 5.4 - Mean Value Theorem for Integrals Find or...Ch. 5.4 - Mean Value Theorem for Integrals Find or...Ch. 5.4 - Mean Value Theorem for Integrals Find or...Ch. 5.4 - Mean Value Theorem for Integrals Find or...Ch. 5.4 - Mean Value Theorem for Integrals Find or...Ch. 5.4 - Explain why or why not Determine whether the...Ch. 5.4 - Planetary orbits The planets orbit the Sun in...Ch. 5.4 - Gateway Arch The Gateway Arch in St. Louis is 630...Ch. 5.4 - Comparing a sine and a quadratic function Consider...Ch. 5.4 - Symmetry of composite functions Prove that the...Ch. 5.4 - Symmetry of composite functions Prove that the...Ch. 5.4 - Prob. 51ECh. 5.4 - Symmetry of composite functions Prove that the...Ch. 5.4 - Prob. 53ECh. 5.4 - Alternative definitions of means Consider the...Ch. 5.4 - Problems of antiquity Several calculus problems...Ch. 5.4 - Prob. 56ECh. 5.4 - Symmetry of powers Fill in the following table...Ch. 5.4 - Bounds on an integral Suppose f is continuous on...Ch. 5.4 - Generalizing the Mean Value Theorem for Integrals...Ch. 5.4 - A sine integral by Riemann sums Consider the...Ch. 5.5 - Find a new variable u so that 4x3(x4+5)10dx=u10du.Ch. 5.5 - In Example 2a, explain why the same substitution...Ch. 5.5 - Evaluate cos6xdxwithout using the substitution...Ch. 5.5 - Evaluate 44x2dx.Ch. 5.5 - Changes of variables occur frequently in...Ch. 5.5 - Review Questions 1. On which derivative rule is...Ch. 5.5 - Why is the Substitution Rule referred to as a...Ch. 5.5 - The composite function f(g(x)) consists of an...Ch. 5.5 - Find a suitable substitution for evaluating...Ch. 5.5 - When using a change of variables u = g(x) to...Ch. 5.5 - If the change of variables u = x2 4 is used to...Ch. 5.5 - Substitution given Use the given substitution to...Ch. 5.5 - Substitution given Use the given substitution to...Ch. 5.5 - Substitution given Use the given substitution to...Ch. 5.5 - Substitution given Use the given substitution to...Ch. 5.5 - Use a substitution of the form u = ax + b to...Ch. 5.5 - Use a substitution of the form u = ax + b to...Ch. 5.5 - Use a substitution of the form u = ax + b to...Ch. 5.5 - Use a substitution of the form u = ax + b to...Ch. 5.5 - Use Table 5.6 to evaluate the following indefinite...Ch. 5.5 - Use Table 5.6 to evaluate the following definite...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - x9sinx10dxCh. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - sec2(10x+7)dxCh. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Definite integrals Use a change of variables or...Ch. 5.5 - Definite integrals Use a change of variables or...Ch. 5.5 - Definite integrals Use a change of variables or...Ch. 5.5 - Definite integrals Use a change of variables or...Ch. 5.5 - Definite integrals Use a change of variables or...Ch. 5.5 - Definite integrals Use a change of variables or...Ch. 5.5 - Definite integrals Use a change of variables or...Ch. 5.5 - Definite integrals Use a change of variables or...Ch. 5.5 - Definite integrals Use a change of variables or...Ch. 5.5 - Definite integrals Use a change of variables or...Ch. 5.5 - Definite integrals Use a change of variables or...Ch. 5.5 - Definite integrals Use a change of variables or...Ch. 5.5 - Definite integrals Use a change of variables or...Ch. 5.5 - Definite integrals Use a change of variables or...Ch. 5.5 - Definite integrals Use a change of variables or...Ch. 5.5 - Definite integrals Use a change of variables or...Ch. 5.5 - Definite integrals Use a change of variables or...Ch. 5.5 - Definite integrals Use a change of variables or...Ch. 5.5 - Definite integrals Use a change of variables or...Ch. 5.5 - 0ln4ex3+2exdxCh. 5.5 - 01x1x2dxCh. 5.5 - Prob. 66ECh. 5.5 - Prob. 67ECh. 5.5 - 06/5dx25x2+36Ch. 5.5 - 02x316x4dxCh. 5.5 - 11(x1)(x22x)7dxCh. 5.5 - 0sinx2+cosxdxCh. 5.5 - 01(v+1)(v+2)2v3+9v2+12v+36dvCh. 5.5 - 1249x2+6x+1dxCh. 5.5 - 0/4esin2xsin2xdxCh. 5.5 - Average velocity An object moves in one dimension...Ch. 5.5 - Periodic motion An object moves along a line with...Ch. 5.5 - Population models The population of a culture of...Ch. 5.5 - Variations on the substitution method Evaluate the...Ch. 5.5 - Variations on the substitution method Find the...Ch. 5.5 - Variations on the substitution method Find the...Ch. 5.5 - Variations on the substitution method Find the...Ch. 5.5 - Variations on the substitution method Find the...Ch. 5.5 - Variations on the substitution method Find the...Ch. 5.5 - Variations on the substitution method Find the...Ch. 5.5 - x(x+10)9dxCh. 5.5 - 033dx9+x2Ch. 5.5 - Integrals with sin2 x and cos2 x Evaluate the...Ch. 5.5 - Integrals with sin2 x and cos2 x Evaluate the...Ch. 5.5 - Integrals with sin2 x and cos2 x Evaluate the...Ch. 5.5 - Integrals with sin2 x and cos2 x Evaluate the...Ch. 5.5 - Integrals with sin2 x and cos2 x Evaluate the...Ch. 5.5 - Integrals with sin2 x and cos2 x Evaluate the...Ch. 5.5 - Integrals with sin2 x and cos2 x Evaluate the...Ch. 5.5 - Prob. 94ECh. 5.5 - Explain why or why not Determine whether the...Ch. 5.5 - Prob. 96ECh. 5.5 - Prob. 97ECh. 5.5 - Areas of regions Find the area of the following...Ch. 5.5 - Prob. 99ECh. 5.5 - Prob. 100ECh. 5.5 - Substitutions Suppose that p is a nonzero real...Ch. 5.5 - Prob. 102ECh. 5.5 - Average value of sine functions Use a graphing...Ch. 5.5 - Equal areas The area of the shaded region under...Ch. 5.5 - Equal areas The area of the shaded region under...Ch. 5.5 - Prob. 106ECh. 5.5 - Prob. 107ECh. 5.5 - Prob. 108ECh. 5.5 - More than one way Occasionally, two different...Ch. 5.5 - Prob. 110ECh. 5.5 - Prob. 111ECh. 5.5 - sin2 ax and cos2 ax integrals Use the Substitution...Ch. 5.5 - Integral of sin2 x cos2 x Consider the integral...Ch. 5.5 - Substitution: shift Perhaps the simplest change of...Ch. 5.5 - Prob. 115ECh. 5.5 - Prob. 116ECh. 5.5 - Prob. 117ECh. 5.5 - Prob. 118ECh. 5.5 - Multiple substitutions If necessary, use two or...Ch. 5 - Explain why or why not Determine whether the...Ch. 5 - Prob. 2RECh. 5 - Ascent rate of a scuba diver Divers who ascend too...Ch. 5 - Use the tabulated values of f to estimate the...Ch. 5 - Estimate 144x+1dx by evaluating the left, right,...Ch. 5 - Prob. 6RECh. 5 - Estimating a definite integral Use a calculator...Ch. 5 - Suppose the expression lim0k=1n(xk3+xk)xk is the...Ch. 5 - Integration by Riemann sums Consider the integral...Ch. 5 - Limit definition of the definite integral Use the...Ch. 5 - Limit definition of the definite integral Use the...Ch. 5 - Limit definition of the definite integral Use the...Ch. 5 - Prob. 13RECh. 5 - Sum to integral Evaluate the following limit by...Ch. 5 - Symmetry properties Suppose that 04f(x)dx=10 and...Ch. 5 - Properties of integrals The figure shows the areas...Ch. 5 - Properties of integrals Suppose that 14f(x)dx=6,...Ch. 5 - Properties of integrals Suppose that 14f(x)dx=6,...Ch. 5 - Properties of integrals Suppose that 14f(x)dx=6,...Ch. 5 - Properties of integrals Suppose that 14f(x)dx=6,...Ch. 5 - Properties of integrals Suppose that 14f(x)dx=6,...Ch. 5 - Properties of integrals Suppose that 14f(x)dx=6,...Ch. 5 - Area by geometry Use geometry to evaluate the...Ch. 5 - Displacement by geometry Use geometry to find the...Ch. 5 - Area by geometry Use geometry to evaluate...Ch. 5 - Use geometry and properties of integrals to...Ch. 5 - Prob. 27RECh. 5 - Prob. 28RECh. 5 - Evaluate the following derivatives. 29....Ch. 5 - Evaluate the following derivatives....Ch. 5 - Evaluate the following derivatives. 31....Ch. 5 - Evaluate the following derivatives. 32....Ch. 5 - Evaluate the following derivatives. 33....Ch. 5 - Evaluate the following derivatives. 34....Ch. 5 - Find the intervals on which f(x)=x1(t3)(t6)11dt is...Ch. 5 - Area function by geometry Use geometry to find the...Ch. 5 - Given that F=f, use the substitution method to...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - 015re3r2+2drCh. 5 - sinzsin(cosz)dzCh. 5 - ex+exdxCh. 5 - Evaluating integrals Evaluate the following...Ch. 5 - dx14x2Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - 02cos2x6dxCh. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Prob. 71RECh. 5 - 33(511x17+302x13+117x9+303x3+x2)dxCh. 5 - 1x2sin1xdxCh. 5 - (tan1x)51+x2dxCh. 5 - dx(tan1x)(1+x2)Ch. 5 - sin1x1x2dxCh. 5 - x(x+3)10dxCh. 5 - x7x4+1dxCh. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - 2/52/5dxx25x21Ch. 5 - sin2x1+cos2xdx (Hint: sin2x=2sinxcosx.)Ch. 5 - 1010x200x2dxCh. 5 - /2/2(cos2x+cosxsinx3sinx5)dxCh. 5 - 04f(x)dx for f(x)={2x+1ifx33x2+2x8ifx3Ch. 5 - 05|2x8|dxCh. 5 - Prob. 87RECh. 5 - Area of regions Compute the area of the region...Ch. 5 - Prob. 89RECh. 5 - Prob. 90RECh. 5 - Prob. 91RECh. 5 - Area versus net area Find (i) the net area and...Ch. 5 - Gateway Arch The Gateway Arch in St Louis is 630...Ch. 5 - Root mean square The root mean square (or RMS) is...Ch. 5 - Displacement from velocity A particle moves along...Ch. 5 - Velocity to displacement An object travels on the...Ch. 5 - Find the average value of f(x)=e2xon [0, ln 2].Ch. 5 - Average height A baseball is launched into the...Ch. 5 - Average values Integration is not needed. a. Find...Ch. 5 - Prob. 100RECh. 5 - An unknown function Assume f is continuous on [2,...Ch. 5 - Prob. 102RECh. 5 - Prob. 103RECh. 5 - Change of variables Use the change of variables u3...Ch. 5 - Prob. 105RECh. 5 - Area functions and the Fundamental Theorem...Ch. 5 - Limits with integrals Evaluate the following...Ch. 5 - Limits with integrals Evaluate the following...Ch. 5 - Prob. 109RECh. 5 - Area with a parameter Let a 0 be a real number...Ch. 5 - Inverse tangent integral Prove that for nonzero...Ch. 5 - Prob. 112RECh. 5 - Prob. 113RECh. 5 - Exponential inequalities Sketch a graph of f(t) =...Ch. 5 - Equivalent equations Explain why if a function u...Ch. 5 - Unit area sine curve Find the value of c such that...Ch. 5 - Unit area cubic Find the value of c0 such that the...
Additional Math Textbook Solutions
Find more solutions based on key concepts
Answer the following regarding the English alphabet. a. Determine the ratio of vowels to consonants. b. What is...
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
To calculate the value of ‘x’ in the figure.
Pre-Algebra Student Edition
Identifying a Test In Exercises 21–24, determine whether the hypothesis test is left-tailed, right-tailed, or t...
Elementary Statistics: Picturing the World (7th Edition)
Females’ Pulse Rates before and after a Fright (Example 17) In a statistics class taught by one of the authors,...
Introductory Statistics
How many outcome sequences are possible ten a die is rolled four times, where we say, for instance, that the ou...
A First Course in Probability (10th Edition)
Explain the meaning of the term “statistically significant difference” in statistics terminology.
Intro Stats, Books a la Carte Edition (5th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Intermediate AlgebraAlgebraISBN:9781285195728Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Intermediate AlgebraAlgebraISBN:9781285195728Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage

Intermediate Algebra
Algebra
ISBN:9781285195728
Author:Jerome E. Kaufmann, Karen L. Schwitters
Publisher:Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Numerical Integration Introduction l Trapezoidal Rule Simpson's 1/3 Rule l Simpson's 3/8 l GATE 2021; Author: GATE Lectures by Dishank;https://www.youtube.com/watch?v=zadUB3NwFtQ;License: Standard YouTube License, CC-BY