
(a)
The number of degrees present in 1 circle.
Answer to Problem 8A
The number of degrees present in 1 circle is 360 degree
Explanation of Solution
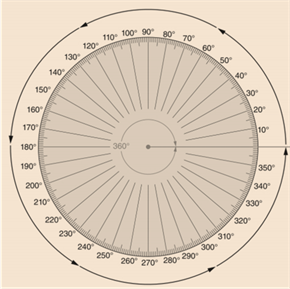
There are 360 degree in 1 circle.
(b)
The total number of minutes in 1degree.
Answer to Problem 8A
Explanation of Solution
A degree is divided into 60-parts called as minutes.
So, the total number of minutes in 1-degree is 60.
(c)
The total number of seconds in 1 minute.
Answer to Problem 8A
Explanation of Solution
A minute is divided into 60-parts called as second.
So, the total number of seconds in 1minute is 60.
(d)
The total number of seconds in 1-degree.
Answer to Problem 8A
The total number of seconds in 1-degree is
Explanation of Solution
so, total number of seconds in 1-degree is
(e)
The total number of minutes in 1-circle.
Answer to Problem 8A
The total number of minutes in 1-circle is
Explanation of Solution
So, the total number of minutes in 1-circle is
Want to see more full solutions like this?
Chapter 50 Solutions
EBK MATHEMATICS FOR MACHINE TECHNOLOGY
- Problem 14 (Orthogonal Matrices). Prove each of the following. 1. P is orthogonal PT is orthogonal. 2. If P is orthogonal, then P-1 is orthogonal. 3. If P, Q are orthogonal, then PQ is orthogonal. Problem 15 (Orthogonal Complement). Consider P2 with the inner product, (f,g) = f(x)g(x)dx. Put W = span(2x+1). Find a basis of W. (1)arrow_forwardProblem 8 (Diagonalization). Let T : P₂ → P₂ be defined as, T(p(x)) = xp'(x). 1. Find the eigenvalues and eigenvectors of T. 2. Show that T is diagonalizable and write P2 as the sum of the eigenspaces of T. Problem 9 (Basis). Determine all the values of the scalar k for which the following four matrices form a basis for M2×2: A₁ = , A2 = k -3 0 , A3 = [ 1 0 -k 2 0 k " A₁ = . -1 -2 Problem 10 (Orthogonality). In this question, we will again see how orthogonality makes computations sim- pler. 1. Let u1,..., un be an (ONB) of a finite-dimensional inner product space V. Let v = c₁u₁ + ... + Сnun and w = d¹µ₁ + ... + dnUn be any two elements of V. Prove that (v, w) = c₁d₁ + ... + Cndn. 2. Write down the corresponding inner product formula for an orthogonal basis.arrow_forwardLet 01(x) = * 0(t) dt, for x > 1, where 0 is Chebyshev's function. Let A1(n) = log n if n is prime, and A₁(n) = 0 otherwise. Prove that 01(x) = (x − n) A1(n), narrow_forwardLet 01 (x) = [* 0(t) dt, for x > 1, where 0 is Chebyshev's function. Let = lim 01(x)/x². 1+00 By considering (t) dt, prove that T-ET 01(x) 01(x Ex) Ex-(x), where = (> 0) is small. - Assuming that 0(x)/x →1 as x → ∞, deduce that (1-1) ≤ 1. By similarly considering (t) dt, prove that (1+½)1 ≥1. 2 Deduce that 01(x) 1½². 2arrow_forwardConsider a rectangular membrane with fixed boundaries of dimensions 5 (horizontal) by 3 (vertical). The deflection u(x, y, t) satisfies the equation utt = 6(uxx + Uyy). (a) Find a formula for the deflection u(x, y, t), if the initial velocity g(x, y) is zero and the initial displacement f(x, y) is f(x, y) = u(x, y, 0) = 2 sin(5πx) sin(лy) - 4 sin(2x) sin(3лy) Do not show the separation of variables. Start with the formula for u(x, y, t). You need to show all details of integration or superposition (if it applies) for credit. (b) Find a numerical approximation for u(5/2, 3/2, 2).arrow_forward(a) Find the general solution to the following differential equation. Express your answer in terms of Bessel functions of the first and second kinds. Do not write any series expansions of these Bessel functions. Please explain how you arrived at your answer. x²y" + xy' + (2x² - 5)y = 0 (b) Solve the heat flow problem. Please start with the formula for u(x, t); Do not show separation of variables. Simplify your answer as much as possible. ди Ət = J²u 2 მე2 u(0,t) = u(5,t) = 0 x, 0 < x <1 u(x, 0): = 1, 1 ≤ x < 4 0, 4≤x≤5arrow_forwardis g(x) = x^4 + x -2 contraction on [0;2]?arrow_forwardConsider the steady state temperature problem over the disk of radius 3 centered at the origin. ▼²u(r, 0) = 0 subject to the following boundary condition: u(3,0) = f(0) = 4 sin³ (0) + 4 cos³ (0) (a) Find u(r, 0). Please go straight to the final formula for u(r, 0); do not show the separation of variables process. You need to show all details of integration or superposition (if it applies) for credit. (b) Approximate numerically u(3/2,π/4).arrow_forward(a) If X is a normal N(2,64) distribution, find k such that P(k ≤ X ≤12) = 0.2957 (b) The random variable T follows a t-distribution with 14 degrees of freedom. Find k such that P(-0.54arrow_forward. (a) A shipment of 30 computers to a store contains 5 that are defective. If the store sells 3 computers, X of which are defective, find the 1. cumulative distribution of X. 2. expected value of X. 3. variance of X. (b) The probability that "heads” will occur in flipping an unfair coin is 2/3. If we flip the coin 5 times, find the probability of obtaining 1. at least 3 heads. 2. at most 3 heads.arrow_forwardnot use ai pleasearrow_forwardChat gpt give wrong answer Plz expert no Chatgptarrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_iosRecommended textbooks for you
 Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning, Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell Elementary AlgebraAlgebraISBN:9780998625713Author:Lynn Marecek, MaryAnne Anthony-SmithPublisher:OpenStax - Rice University
Elementary AlgebraAlgebraISBN:9780998625713Author:Lynn Marecek, MaryAnne Anthony-SmithPublisher:OpenStax - Rice University
 Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning, Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell Elementary AlgebraAlgebraISBN:9780998625713Author:Lynn Marecek, MaryAnne Anthony-SmithPublisher:OpenStax - Rice University
Elementary AlgebraAlgebraISBN:9780998625713Author:Lynn Marecek, MaryAnne Anthony-SmithPublisher:OpenStax - Rice University