
Concept explainers
5.137 and 5.138 Locate the centroid of the plane area shown.
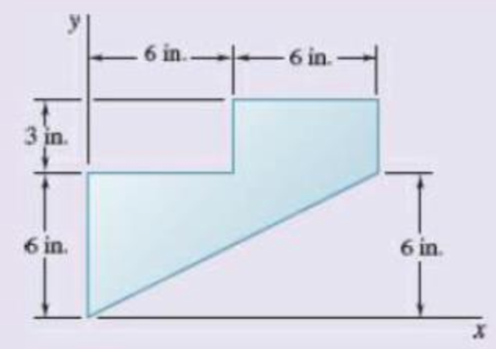
Fig. P5.137
The centroid of the plane shown.
Answer to Problem 5.137RP
The centroid of the plane area
Explanation of Solution
Refer Figure 1.
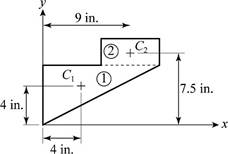
The plane is considered as two separate sections as in figure 1. Section 1 is a perpendicular triangle and section 2 is a rectangle.
Write an expression to calculate the area of section 1.
Here,
Write an expression to calculate the area of section 2.
Here,
Write an expression to calculate the area of the plane.
Here,
Write an expression to calculate the x component of the centroid of the plane.
Here,
There are two sections in the plane. Rewrite equation (IV) according to the plane.
Here,
Write an expression to calculate the y component of the centroid of the plane.
Here,
There are two sections in the plane. Rewrite equation (VI) according to the plane.
Here,
Conclusion:
Substitute
Substitute
Substitute
Substitute
Substitute
Thus, the centroid of the plane area
Want to see more full solutions like this?
Chapter 5 Solutions
VECTOR MECH...,STAT.+DYN.(LL)-W/ACCESS
- 5.8 Locate the centroid of the plane area shown. 16 in. + 20 in. r = 38 in.arrow_forwardLocate the center of gravity of the sheet-metal form shown.arrow_forwardThe horizontal x axis is drawn through the centroid C of the area shown, and it divides the area into two component areas A1 and A2. Determine the first moment of each component area with respect to the x axis, and explain the results obtained. 7.5 in. A1 C A2 4.5 in. 4.5 in. Fig. P5.21arrow_forward
- Determine by direct integration the centroid of the area shown. Fig. P5.34 y h Xarrow_forward5.35 Determine by direct integration the centroid of the area shown. y 3/2 = kx¹/2 ^y₁ = mx b Xarrow_forwardFor the semiannular area of Prob. 5.12, determine the ratio r1 to r2 so that the centroid of the area is located at x = -1/2 r2 and y= 0.(Reference to Problem 5.12):Locate the centroid of the plane area shown.arrow_forward
- The composite body shown is formed by removing a semi ellipsoid of revolution of semi major axis h and semiminor axis a/2 from a hemisphere of radius a. Determine (a)the ij coordinate of the centroid when h=a/2, (b) the ratio h/a for which ij =—0,4a.arrow_forwardDetermine the volume of the solid obtained by rotating the area of Prob. 5.4 about (a) the x axis, (b) the y axis.arrow_forward5.115 and 5.116 Locate the center of gravity of the figure shown, knowing that it is made of thin brass rods of uniform diameter. B D Fig. P5.116 r = 16 in. E 30 in.arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





