EBK ELECTRIC CIRCUITS
10th Edition
ISBN: 8220100801792
Author: Riedel
Publisher: YUZU
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Question
Chapter 5, Problem 1P
(a)
To determine
Label the five terminals in the operational amplifier.
(a)
Expert Solution
Explanation of Solution
Given data:
Refer to Figure P5.1 in the textbook for the ideal op amp circuit.
Discussion:
The five terminals of the op amp are labeled as shown in Figure 1.
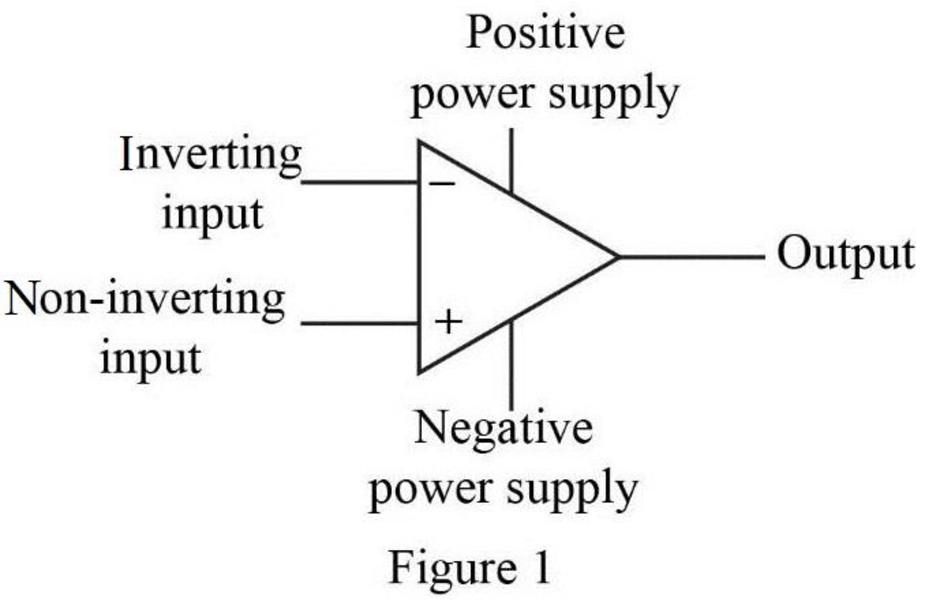
Conclusion:
Thus, the five op-amp terminals with their names are labeled as shown in Figure 1.
(b)
To determine
Mention the ideal op amp constraint that determines the value of
(b)
Expert Solution
Answer to Problem 1P
The input resistance of the op amp constraints determines the value of
Explanation of Solution
Discussion:
The input resistance available at the input terminals will determines the current value
Conclusion:
Thus, the input resistance of the op amp constraints determines the value of
(c)
To determine
Mention the ideal op amp constraints that determines the value of
(c)
Expert Solution
Answer to Problem 1P
The open loop voltage gain of the op amp constraints the value of
Explanation of Solution
Discussion:
The open loop voltage gain of an ideal op amp determines the value of
Conclusion:
Thus, the open loop voltage gain of the op amp constraints the value of
(d)
To determine
Find the value of voltage
(d)
Expert Solution
Answer to Problem 1P
The value of voltage
Explanation of Solution
PSpice Simulation:
Draw the given circuit in PSPICE as shown in Figure 1.
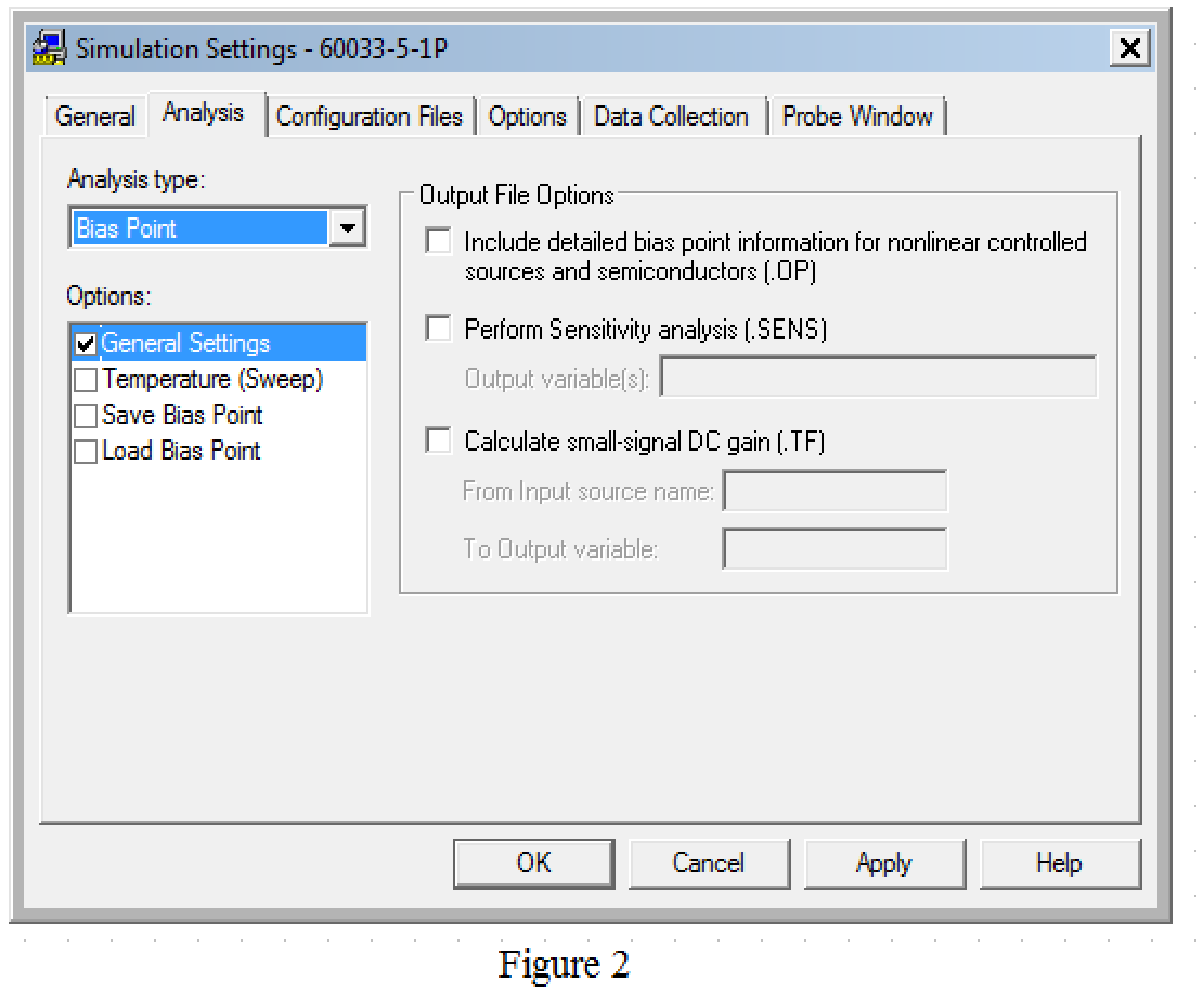
Provide the simulation settings as shown in Figure 2 to obtain output parameters.
After simulating the PSPICE circuit, the output voltage
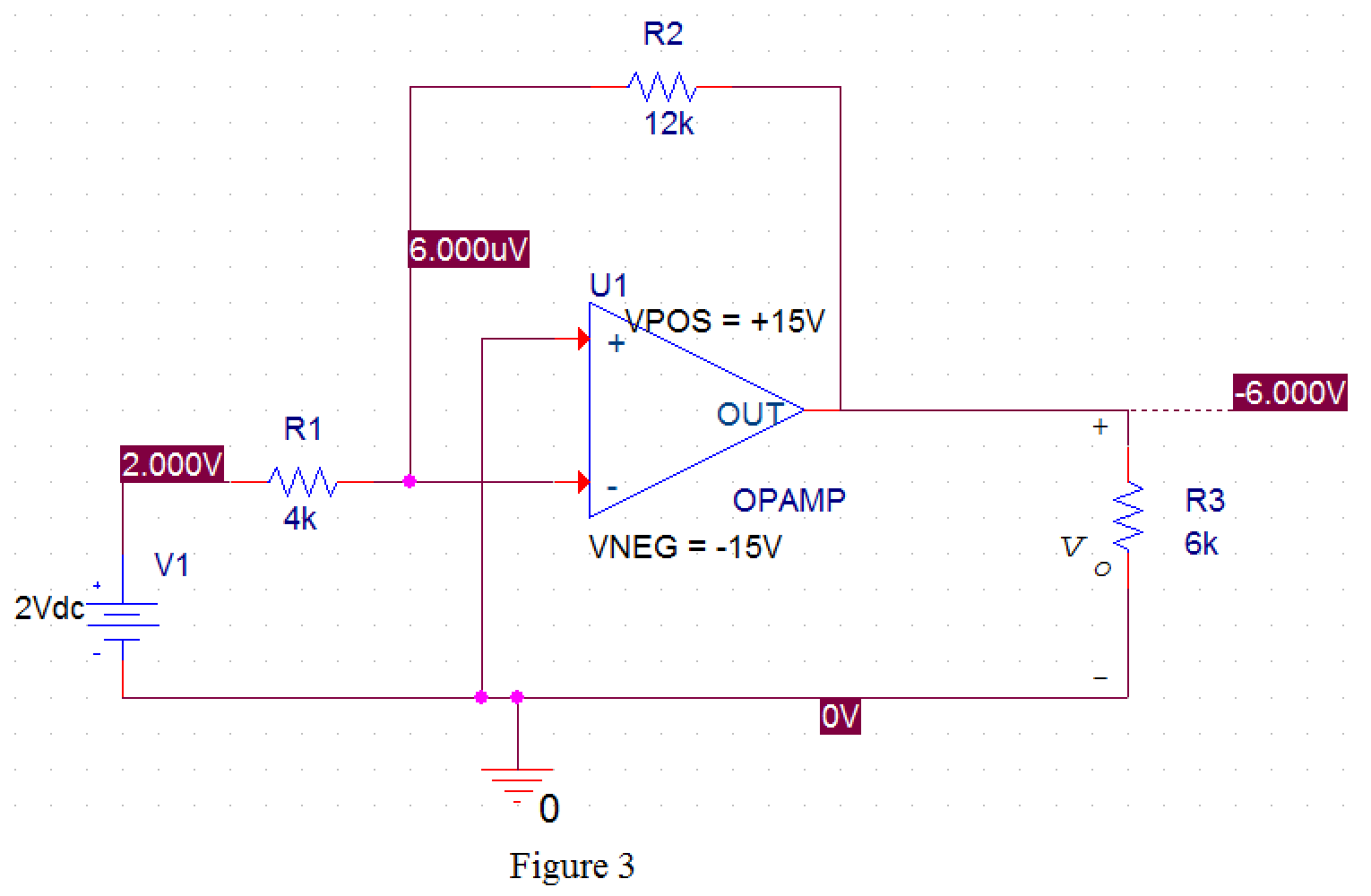
From Figure 3, the value of output voltage is
Conclusion:
Thus, the value of voltage
Want to see more full solutions like this?
Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!
Students have asked these similar questions
control system
G = X^4+X+1
M = X^9+X^8+X^6+X^4+X^3+X+1
2.52. The step response s(t) of a continuous-time LTI system is given by
s(1) = [cos wol ]u(1)
Find the impulse response h(t) of the system.
Ans. h(t)=8(1) - wo[sin w₁t]u(t)
Chapter 5 Solutions
EBK ELECTRIC CIRCUITS
Ch. 5.2 - Assume that the op amp in the circuit shown is...Ch. 5.3 - The source voltage vs in the circuit in Assessment...Ch. 5.4 - Find vo in the circuit shown if va = 0.1 V and vb...Ch. 5.5 - Assume that the op amp in the circuit shown is...Ch. 5.6 - In the difference amplifier shown, vb = 4.0 V....Ch. 5.7 - The inverting amplifier in the circuit shown has...Ch. 5 - Prob. 1PCh. 5 - Replace the 2 V source in the circuit in Fig. P5.1...Ch. 5 - Find iL (in milliamperes) in the circuit in Fig....Ch. 5 - The op amp in the circuit in Fig. P5.4 is...
Ch. 5 - Find io in the circuit in Fig. P5.3 if the op amp...Ch. 5 - The op amp in the circuit in Fig. P5.5 is ideal....Ch. 5 - Prob. 7PCh. 5 - Design an inverting amplifier with a gain of 4....Ch. 5 - Design an inverting amplifier with a gain of 2.5,...Ch. 5 - The op amp in the circuit shown in Fig. P5.11 is...Ch. 5 - The op amp in the circuit in Fig. P5.10 is...Ch. 5 - The op amp in Fig. P5.12 is ideal.
What circuit...Ch. 5 - Refer to the circuit in Fig. 5.12, where the op...Ch. 5 - The op amp in Fig. P5.14 is ideal. Find vo if va =...Ch. 5 - Prob. 15PCh. 5 - Design an inverting-summing amplifier using a 120...Ch. 5 - Design an inverting-summing amplifier so...Ch. 5 - Prob. 18PCh. 5 - The op amp in the circuit of Fig. P5.18 is...Ch. 5 - Prob. 20PCh. 5 - Prob. 21PCh. 5 - Prob. 22PCh. 5 - Prob. 23PCh. 5 - The circuit in Fig. P5.24 is a noninverting...Ch. 5 - Prob. 25PCh. 5 - The op amp in the circuit of Fig. P5.25 is...Ch. 5 - The resistors in the difference amplifier shown in...Ch. 5 - Prob. 28PCh. 5 - Prob. 29PCh. 5 - The op amp in the adder-subtracter circuit shown...Ch. 5 - Select the values of Rb and Rf in the circuit in...Ch. 5 - The op amp in the circuit of Fig. P5.34 is...Ch. 5 - Prob. 33PCh. 5 - In the difference amplifier shown in Fig. P5.34,...Ch. 5 - Prob. 36PCh. 5 - Show that when the ideal op amp in Fig. P5.38 is...Ch. 5 - Assume that the ideal op amp in the circuit seen...Ch. 5 - The two op amps in the circuit in Fig. P5.40 are...Ch. 5 - Assume that the ideal op amp in the circuit in...Ch. 5 - The op amps in the circuit in Fig. P5.39 are...Ch. 5 - The circuit inside the shaded area in Fig. P5.41...Ch. 5 - Derive Eq. 5.31.
(5.31)
Ch. 5 - Prob. 44PCh. 5 - Prob. 45PCh. 5 - Repeat Problem 5.45 assuming an ideal op...Ch. 5 - Prob. 47PCh. 5 - The op amp in the noninverting amplifier circuit...Ch. 5 - Suppose the strain gages in the bridge in Fig....Ch. 5 - For the circuit shown in Fig. P5.50, show that if...Ch. 5 - Prob. 51PCh. 5 - Prob. 52PCh. 5 - Prob. 53P
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, electrical-engineering and related others by exploring similar questions and additional content below.Similar questions
- 2.48. Show that if y(t) = x(t)* h(t), then y' (t) = x' (1) * h(t) = x(t) * h'(t) Hint: Differentiate Eqs. (2.6) and (2.10) with respect to t. 2.49. Show that x(1) * 8'(t) = x(t) Hint: Use the result from Prob. 2.48 and Eq. (2.58).arrow_forward2.47. Compute the convolution sum y[n] = x[n]+h[n] of the following pairs of sequences: (a) x[n] = u[n], h[n] = 2"u[n] (b) x[n]=u[n]-u[n-N], h[n]=a"u[n], 0 < a <1 (c) x[n]=()"u[n], h[n] = 8[n] - 8[n-1]arrow_forward2.55. Consider a discrete-time LTI system with impulse response h[n] given by Is this system memoryless? Ans. No, the system has memory. h[n] = [n-1]arrow_forward
- "4. The load impedance connected to the secondary winding of the ideal transformer in the following circuit consists of a resistance of 237.5m2 in series with an inductor of 125µH. If the sinusoidal voltage source v, is generating the voltage 2500 cos(400t) V, calculate the steady-state equations for: (a) 21. (b) v1. (c) i₂, and (d) v2." 08 0,255 mH 237,5 m2 10:1 01 - Ideal 02 125 pharrow_forward2.55. Consider a discrete-time LTI system with impulse response h[n] given by h[n]=8[n-1] Is this system memoryless? Ans. No, the system has memory.arrow_forward"1. Formulate the matrix system to find the voltages and currents of the transformer in the following circuit. Hint: Use KVL (Kirchhoff's Voltage Law) in each winding of the transformer and use the voltage and current relationships." RT www pNp Ns Rc Vp idealarrow_forward
- 2.62. Write the input-output equation for the system shown in Fig. 2-34. Ans. 2y[n]-y[n-1] = 4x[n] + 2x[n-1] x[n] Unit delay Fig. 2-34 y[n] Σ + +arrow_forward(ii) Register B hold the data byte 28H and accumulator hold 97H. Show the contents of the registers B, C and accumulator after the execution of the following instructions. MOV A, B MOV C, Aarrow_forward2.53. The system shown in Fig. 2-31 is formed by connection two systems in parallel. The impulse responses of the systems are given by h₁(t)=eu(1) and h₂(1) = 2e'u(1) (a) Find the impulse response h(t) of the overall system. (b) Is the overall system stable? Ans. (a) h(t) = (e-21 + 2e')u(t) (b) Yes x(t) h₁(1) + h₂(1) Fig. 2-31 + y(t) Σarrow_forward
- 2.54. Consider an integrator whose input x(t) and output y(t) are related by y(t) = '_x(T) dT (a) Find the impulse response h(t) of the integrator. (b) Is the integrator stable? Ans. (a) h(t) = u(t) (b) Noarrow_forward2.61. Is the system described by the differential equation linear? Ans. No, it is nonlinear. dy(t) +5y(1)+2=x(1) dtarrow_forward2.64. Consider a discrete-time system whose input x[n] and output y[n] are related by y[n] y[n-1] = x[n] with y[-1] = 0. Find the output y[n] for the following inputs: (a) x[n]=()u[n]; (b) x[n]=()u[n] Ans. (a) y[n] = 6[()*+' - (¹)" + ¹]u[n] (b) y[n] = (n+1X)"u[n]arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON
Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning
Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education
Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON
Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,
Introductory Circuit Analysis (13th Edition)
Electrical Engineering
ISBN:9780133923605
Author:Robert L. Boylestad
Publisher:PEARSON
Delmar's Standard Textbook Of Electricity
Electrical Engineering
ISBN:9781337900348
Author:Stephen L. Herman
Publisher:Cengage Learning
Programmable Logic Controllers
Electrical Engineering
ISBN:9780073373843
Author:Frank D. Petruzella
Publisher:McGraw-Hill Education
Fundamentals of Electric Circuits
Electrical Engineering
ISBN:9780078028229
Author:Charles K Alexander, Matthew Sadiku
Publisher:McGraw-Hill Education
Electric Circuits. (11th Edition)
Electrical Engineering
ISBN:9780134746968
Author:James W. Nilsson, Susan Riedel
Publisher:PEARSON
Engineering Electromagnetics
Electrical Engineering
ISBN:9780078028151
Author:Hayt, William H. (william Hart), Jr, BUCK, John A.
Publisher:Mcgraw-hill Education,
Electrical Engineering: Ch 5: Operational Amp (2 of 28) Inverting Amplifier-Basic Operation; Author: Michel van Biezen;https://www.youtube.com/watch?v=x2xxOKOTwM4;License: Standard YouTube License, CC-BY