
Interpretation:
To sketch the super-current Ic sin ϕ (t) as a function of t assuming that IIc is slightly greater than 1 and IIc >> 1, for a Josephson junction in the over-damped limit β = 0. To sketch the instantaneous voltage V(t) for both the cases
Concept Introduction:
The Josephson relation in the over-damped limit β = 0 is given by ˙ϕ = IIc - sin ϕ.
Josephson voltage-phase relation is given by V = ℏ2e˙ϕ
Answer to Problem 1E
Solution:
a) The super-current Ic sin ϕ (t) as a function of t assuming that IIc is slightly greater than 1 and IIc >> 1 for a Josephson junction in the over-damped limit β = 0 is sketched.
b) The instantaneous voltage V(t) for both the cases is sketched.
Explanation of Solution
Josephson junctions are superconducting devices that are capable of generating voltage oscillations of extraordinarily high frequency. It consists of two closely spaced superconductors separated by a weak connection.
The Josephson relation in the over-damped limit β = 0 is given by
˙ϕ = IIc - sin ϕ
Here, Ic is the critical current.
Assuming that IIc is slightly greater than 1
Consider IIc = 1.1
˙ϕ = 1.1 - sin ϕ
The graph of ϕ vs. t is shown below
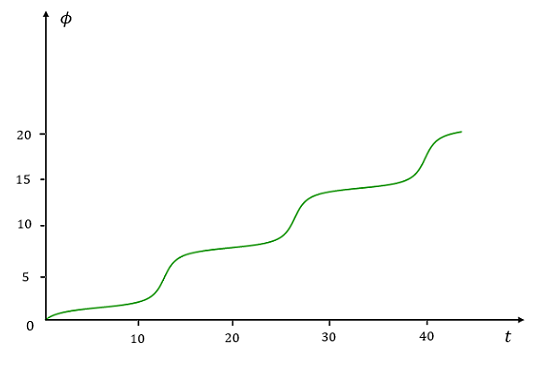
Assuming that IIc >> 1.
Consider IIc = 10,
ϕ′ = 10 - sin ϕ
The graph of ϕ vs. t is shown below.
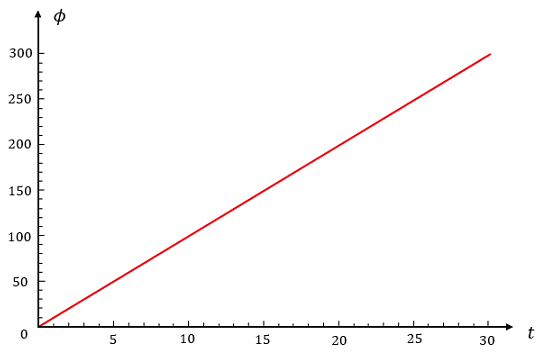
b) Josephson voltage-phase relation is given by
V = ℏ2e˙ϕ
Substituting ˙ϕ = IIc - sin ϕ, we get
V = ℏ2e(IIc - sin ϕ)
Consider IIc = 1.1
The graph of voltage vs. ϕ is shown below.
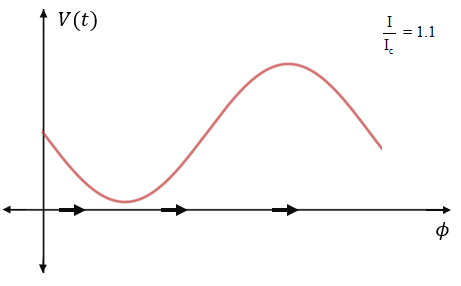

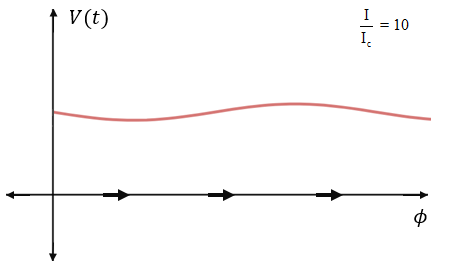
V = ℏ2e(IIc - sin ϕ)
Consider IIc = 10
The graph of voltage vs. ϕ is shown below.

Want to see more full solutions like this?
Chapter 4 Solutions
Nonlinear Dynamics and Chaos
- 25.2. Find the Laurent series for the function 1/[z(z-1)] in the follow- ing domains: (a). 0<|z|< 1, (b). 1<|z, (c). 0arrow_forward25.5. Find the Laurent series for the function 1/[(z - 1)(-2)(z - 3)] in the following domains: (a). 0 3. شهریarrow_forward25.1. Expand each of the following functions f(z) in a Laurent series on the indicated domain: (a). z² - 2z+5 (2-2)(z² + 1)' (c). Log za 2 b (z - موجود 11, 29, where b>a> 1 are real, |z| > b.arrow_forward
- 25.3. Find the Laurent series for the function z/[(22 + 1)(z² + 4)] in the following domains (a). 02.arrow_forward25.2. Find the Laurent series for the function 1/[z(z-1)] in the follow- ing domains: (a). 0<|z|< 1, (b). 1 <|z|, (c). 0<|z1|< 1, (d). 1< |z1|, (e). 1<|z2|<2.arrow_forward25.1. Expand each of the following functions f(z) in a Laurent series on the indicated domain: 22-2z+5 (z - 2) (z² + 1)' (z 11, 22 (a). (c). Log (2-8) where b>a> 1 are real, |z|> b. barrow_forward
- 25.5. Find the Laurent series for the function 1/[(2-1)(z-2)(z-3)] in the following domains: (a). 0 3.arrow_forwardCan you explain how the error term in the CF Algorithm relates to the (m+1)th complete quotient? Also, what would be a good way to explain the connection between these two slides? How can one transition between them for a presentation?arrow_forwardHow can I explain the pi example in a presentation? I'm having trouble transitioning between these two slidesarrow_forward
- McGilla Golf has decided to sell a new line of golf clubs. The clubs will sell for $895 per set and have a variable cost of $431 per set. The company has spent $200,000 for a marketing study that determined the company will sell 80,000 sets per year for seven years. The marketing study also determined that the company will lose sales of 8,600 sets per year of its high-priced clubs. The high-priced clubs sell at $1,325 and have variable costs of $645. The company will also increase sales of its cheap clubs by 10,800 sets per year. The cheap clubs sell for $340 and have variable costs of $141 per set. The fixed costs each year will be $14,350,000. The company has also spent $1,500,000 on research and development for the new clubs. The plant and equipment required will cost $43,700,000 and will be depreciated on a straight-line basis. The new clubs will also require an increase in net working capital of $3,625,000 that will be returned at the end of the project. The tax rate is 25…arrow_forwardTri-County Utilities, Inc., supplies natural gas to customers in a three-county area. The company purchases natural gas from two companies: Southern Gas and Northwest Gas. Demand forecasts for the coming winter season are as follows: Hamilton County, 400 units; Butler County, 200 units; and Clermont County, 300 units. Contracts to provide the following quantities have been written: Southern Gas, 500 units; and Northwest Gas, 400 units. Distribution costs for the counties vary, depending upon the location of the suppliers. The distribution costs per unit (in thousands of dollars) are as follows. From To Hamilton Butler Clermont Southern Gas 10 20 15 Northwest Gas 12 15 18 (a) Develop a network representation of this problem. (Submit a file with a maximum size of 1 MB.) Choose File No file chosen Assignment 3 graph.docx Score: 1 out of 1 Comment: (b) Develop a linear programming model that can be used to determine the plan that will minimize total distribution costs (in thousands of…arrow_forwardUse the method of undetermined coefficients to solve the given nonhomogeneous system. dx dt = 2x + 3y − 8 dy dt = −x − 2y + 6 X(t) =arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
