
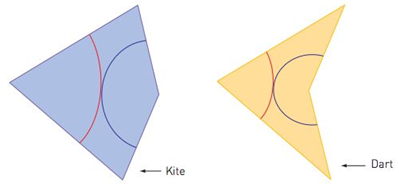
Penrose tiles. Roger Penrose constructed two tiles that can be used to cover the plane only in aperiodic ways. One tile is called a kite, one is called a dart. Show how to construct a tiling using these tiles. Notice that each tile contains both a blue and red arc. The only rule for assembling the tiles is that the ends of blue arcs must touch only the ends of other blue arcs and ends of red arcs must touch only the ends of other red arcs. Given this rule and using many copies of the kites and darts, show how to construct a tiling using these two tiles.
Want to see the full answer?
Check out a sample textbook solution
Chapter 4 Solutions
The Heart of Mathematics: An Invitation to Effective Thinking
Additional Math Textbook Solutions
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Thinking Mathematically (6th Edition)
Elementary Statistics (13th Edition)
Algebra and Trigonometry (6th Edition)
Using and Understanding Mathematics: A Quantitative Reasoning Approach (6th Edition)
University Calculus: Early Transcendentals (4th Edition)
- A television network earns an average of $14 million each season from a hit program and loses an average of $8 million each season on a program that turns out to be a flop. Of all programs picked up by this network in recent years, 25% turn out to be hits and 75% turn out to be flops. At a cost of C dollars, a market research firm will analyze a pilot episode of a prospective program and issue a report predicting whether the given program will end up being a hit. If the program is actually going to be a hit, there is a 75% chance that the market researchers will predict the program to be a hit. If the program is actually going to be a flop, there is only a 30% chance that the market researchers will predict the program to be a hit. What is the maximum value of C that the network should be willing to pay the market research firm? Enter your answer in dollars, not in million dollars. $ __________ Calculate EVPI for this decision problem. Enter your answer in dollars, not in million…arrow_forwardEvaluate the line integral sin z dz, So sin where C is the portion of the curve y = x² from 0 to −1 + i.arrow_forwardLet f(z) be complex differentiable everywhere in C. Fix two distinct complex numbers a and b and a circle C of radius R with |a| < R,|b| < R traversed in the counter-clockwise direction. Evaluate the integral Sc − f(z)dz (z - a)(z – b) in terms of a, b and the values of f at those points.arrow_forward
- | Let C be a circle (with a positive radius) such that z = 1 lies in its interior. Evaluate the contour integral So Tz zez (z - 1)³ = where C is traversed in the clockwise direction. dzarrow_forwardquestion 8arrow_forwardTwo construction companies are bidding against one another for the right to construct a new community center building. The first construction company, Fine Line Homes, believes that its competitor, Buffalo Valley Construction, will place a bid for this project according to the distribution shown in this table: Buffalo Valley's Bid Bid Probability $160,000 0.2 $165,000 0.5 $170,000 0.2 $175,000 0.1 Furthermore, Fine Line Homes estimates that it will cost $160,000 for its own company to construct this building. Given its fine reputation and long-standing service within the local community, Fine Line Homes believes that it will likely be awarded the project in the event that it and Buffalo Valley Construction submit exactly the same bids. Find the bid that maximizes Fine Line’s expected profit. Max expected profit $ ________ . Bid that maximizes profit $ ________ .arrow_forward
 Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGALAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGALAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
 College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning





