
Concept explainers
(a)
To show: The point where
(a)
Answer to Problem 38.72AP
Explanation of Solution
Given info: The equation of the intensity of the light in the diffraction pattern is
The formula to calculate the intensity of the light is,
Here,
The value of
Substitute
Conclusion
Therefore, the point where
(b)
To draw: Plot
(b)
Answer to Problem 38.72AP
The graph between
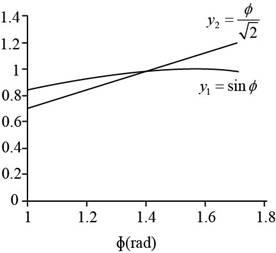
Figure (1)
Explanation of Solution
Given info: The equation of the intensity of the light in the diffraction pattern is
The equation of
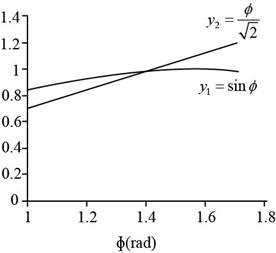
The solution of both the equation to coincide at a point is ,
So the solution of the transcendental equation is
(c)
To show: The angular full width at half maximum of the central diffraction maximum is
(c)
Answer to Problem 38.72AP
Explanation of Solution
Given info: The equation of the intensity of the light in the diffraction pattern is
The formula to calculate the phase angle is,
Rewrite the above equation for
If the value of
The path covered by the light is symmetric so the phase angle is double the initial value.
Substitute
Conclusion
Therefore, the angular full width at half maximum of the central diffraction maximum is
(d)
The number of steps involved to solve the transcendental equation ϕ = 2 sin ϕ
(d)
Answer to Problem 38.72AP
Explanation of Solution
Given info: The equation of the intensity of the light in the diffraction pattern is
The equation of
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The solution of the transcendental equation
Conclusion
Therefore, the number of steps involved to solve the transcendental equation
Want to see more full solutions like this?
Chapter 38 Solutions
Physics for Scientists and Engineers, Technology Update (No access codes included)
- A piece of silicon semiconductor has length L=0.01cm and cross-section in a square shape with an area of A=5×10−4cm2 . The semiconductor is doped with 1012cm−3 Phosphorus atoms and 1017cm−3 Boron atoms. An external electric field E=1.5×104N/C is applied to the silicon piece along the length direction, through the cross section. What is the total current in the silicon at T=300K? Assume the mobility of silicon is 1400cm2V−1s−1 for electrons and 450cm2V−1s−1 for holes, respectively. Assume the intrinsic carrier concentration in silicon is 1010cm−3 . Give your answer in mA, rounded to 3 significant figures. Just enter the number, nothing else.arrow_forwardAn impurity with a charge of 2e is placed in a three-dimensional metal. Assume that the Friedel sum rule holds for this system, and only the scattering phase shifts from the electrons contribute to this sum (we don't need to consider ion phase shifts). This metal has a spherical Fermi surface with Fermi wave vector kF . The only degeneracy for the electrons at the Fermi surface is spin (two-fold) and angular momentum ( 2l+1 for each angular momentum l ). Ignore scattering for l>2 and assume that the scattering doesn't depend on the spin degree of freedom. Denote the scattering phase shift at the Fermi wave vector in the l -th angular momentum channel as δl(kF) . If δ0(kF)=11π31 , and δ1(kF)=π29 , what is δ2(kF)? Round your answer to three significant figures. Just enter the number, nothing else.arrow_forwardA pilot with a mass of 75 kg is flying an airplane at a true airspeed of 55m/s in air that is still relative to the ground. The pilot enters a coordinated turn of constant bank angle and constant altitude, and the pilot experiences an effective weight of 1471.5N normal to the wings of the plane. What is the rate of turn (in degrees per second) for the aircraft? Round your answer to three significant figures. Just enter the number, nothing else.arrow_forward
- Imagine you are out for a stroll on a sunny day when you encounter a lake. Unpolarized light from the sun is reflected off the lake into your eyes. However, you notice when you put on your vertically polarized sunglasses, the light reflected off the lake no longer reaches your eyes. What is the angle between the unpolarized light and the surface of the water, in degrees, measured from the horizontal? You may assume the index of refraction of air is nair=1 and the index of refraction of water is nwater=1.33 . Round your answer to three significant figures. Just enter the number, nothing else.arrow_forwardRed, yellow, green, and blue light with wavelengths of λred=700 nm , λyellow=580 nm , λgreen=520 nm , and λblue=475 nm are directed at a slit that is 20 μm wide at normal incidence. The light hits a screen 1 m behind the slit. Which color of light will have an interference minimum closest to a point 10 cm away from its central maxima? You may assume the small angle approximation sinθ≈tanθ≈θ for angles smaller than 10∘ . Just enter the wavelength of that color in nm, nothing else.arrow_forwardIn the circuit shown, the switch is initially open and the capacitor isuncharged. What will be the current through R1 the instant after the switch isclosed? Take V=10 V, R1 = 20 W, R2 = 20 W, R3 = 10 W and C = 2 mF.arrow_forward
 University Physics Volume 3PhysicsISBN:9781938168185Author:William Moebs, Jeff SannyPublisher:OpenStax
University Physics Volume 3PhysicsISBN:9781938168185Author:William Moebs, Jeff SannyPublisher:OpenStax
