Chapter 3.7, Problem 9P

Problems 7 through 10 deal with the RC circuit in Fig. 3.7.8, containing a resistor (R ohms), a capacitor (C farads), a switch, a source of emf, but no inductor Substitution of $L=0$ in Eq. (3) gives the linear first-order differential equation $R\frac{dQ}{dt}+\frac{1}{C}Q=E\left(t\right)$

for the charge $Q=Q\left(t\right)$ on the capacitor at time t. Note that $I\left(t\right)=Q\text{'}\left(t\right)$ .

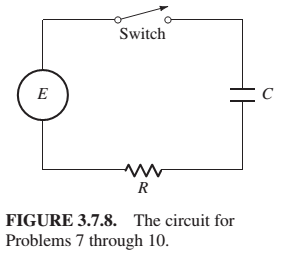
Suppose that in the circuit of Fig. 3.7.8, $R=200,C=2.5\times {10}^{-4},Q\left(10\right)=0,\text{and}E\left(t\right)=100\cos 120t$. (a) Find Q (t ) and I (t ). (b) What is the amplitude of the steady-state current?