
Concept explainers
Pierre de Fermat (1601–1665) showed that whenever light travels from one point to another, its actual path is the path that requires the smallest time interval. This statement is known as Fermat’s principle. The simplest example is for light propagating in a homogeneous medium. It moves in a straight line because a straight line is the shortest distance between two points. Derive Snell’s law of refraction from Fermat’s principle. Proceed as follows. In Figure P34.54, a light ray travels from point P in medium 1 to point Q in medium 2. The two points are, respectively, at perpendicular distances a and b from the interface. The displacement from P to Q has the component d parallel to the interface, and we let x represent the coordinate of the point where the ray enters the second medium. Let t = 0 be the instant the light starts from P. (a) Show that the time at which the light arrives at Q is
(b) To obtain the value of x for which t has its minimum value, differentiate t with respect to x and set the derivative equal to zero. Show that the result implies
(c) Show that this expression in turn gives Snell’s law.
Figure P34.54 Problems 54 and 55.
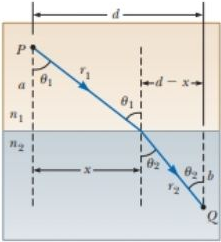
(a)
To show: The time at which the light arrives at Q is
Answer to Problem 35.84CP
Explanation of Solution
The given figure is shown below.
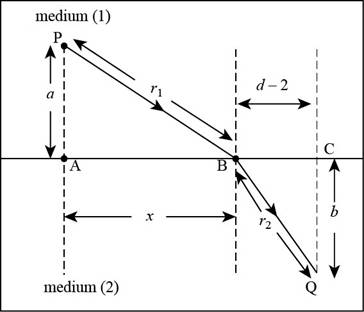
Figure (1)
In right angle triangle PAB,
In right angle triangle BCQ,
The time taken by light to travel from point P to Q is,
Here,
The expression for refractive index is,
Substitute
Substitute
Substitute
Conclusion:
Therefore, the time at which the light arrives at Q is
(b)
To show: The result
Answer to Problem 35.84CP
Explanation of Solution
Apply the condition of maxima and minima,
Substitute
Conclusion:
Therefore, the result
(c)
To show: The expression of Snell’s law,
Answer to Problem 35.84CP
Explanation of Solution
In right angle triangle PAB,
Similarly, in right angle triangle BCQ,
Substitute,
Conclusion:
Therefore, the expression of Snell’s law is
Want to see more full solutions like this?
Chapter 35 Solutions
Physics for Scientists and Engineers, Technology Update (No access codes included)
- A beam of light traveling in air strikes a slab of transparent material. The incident beam makes an angle of 60° with the normal, and the refracted beam make an angle of 50° with the normal. What is the speed of light in the transparent material? (c = 3.0 × 108 m/s) Provide the answer: x 108 m/sarrow_forwardAn incident light ray is aimed at the open top of a tank filled with Benzene, kerosene and glycerin. Determine the angle of incidence and refraction of the light at the 1st and 3rd mediums if the angle in the 2nd medium is 20°. The indices of refraction for kerosene and glycerin are 1.39 and 1.46 respectively. What is the index of refraction of the first medium if the light ray travels the first medium at is 2 x 10^8 m/s.arrow_forwardA beam of light traveling through a liquid (of index of refraction n1 = 1.51) is incident on a surface at an angle of θ1 = 59° with respect to the normal to the surface. It passes into the second medium and refracts at an angle of θ2 = 69° with respect to the normal. a) What is the index of refraction of the second material? b) Numerically, what is the light's velocity in medium 1, in meters per second? c) Numerically, what is the light's velocity in medium 2, in meters per second?arrow_forward
- As sunlight enters the Earth’s atmosphere, it changes direction due to the small difference between the speeds of light in vacuum and in air. The duration of an optical day is defined as the time interval between the instant when the top of the rising Sun is just visible above the horizon andthe instant when the top of the Sun just disappears below the horizontal plane. The duration of the geometric day is defined as the time interval between the instant a mathematically straight line between an observer and the top of the Sun just clears the horizon and the instant this linejust dips below the horizon. (a) Explain which is longer, an optical day or a geometric day. (b) Find the difference between these two time intervals. Model the Earth’s atmosphere as uniform, with index of refraction 1.000 293, a sharply defined upper surface, and depth 8 614 m. Assume the observer is at the Earth’s equator so that the apparent path of the rising and setting Sun is perpendicular to the horizon.arrow_forwardWhen a ray of light changes media , it will refract (bend). With angles being measured from the normal, the amount of refraction can be found using Snell's Law . Traveling through any medium light will have a speed given by the equation shown where n represents the index of refraction and is the speed of light in a vacuum (3 * 10 ^ 8 * m/c) . A) In the picture of refraction shown which index of refraction is larger n1 or n2 B)In what medium does the lightbeam shown travel faster C) Measure the angles, Assuming n1 refers to vaccum what is the value of n2? How fast does light travel within n2?arrow_forwardConsider the following situation for the next two problems. A piece of transparent material with unknown index of refraction is immersed in water (n = 1.333). A ray of light propagating within the material strikes the top surface at an angle of 0, = 58° as shown below and undergoes total internal reflection. This is the smallest incident angle for which total internal reflection can occur. The reflected ray then hits the right side of the material and enters the surrounding water at an angle of 0,. Note: Figure not to scale. water 0f 2-15 What is the index of refraction of the transparent material? (± 0.002)arrow_forward
- A beam of light traveling through a liquid (of index of refraction n1 = 1.3) is incident on a surface at an angle of θ1 = 55° with respect to the normal to the surface. It passes into the second medium and refracts at an angle of θ2 = 65° with respect to the normal. Part (a) Write an equation for the index of refraction of the second material. Part (b) What is the index of refraction of the second material? Part (c) Numerically, what is the light's velocity in medium 1, in meters per second? Part (d) Numerically, what is the light's velocity in medium 2, in meters per second?arrow_forwardConsider a layer of Oil, Glass, and Air where the oil/glass boundary is parallel to the glass/air boundary. Let the index of refraction for the glass be 1.55 and the index of refraction for the oil to be 1.31. At what angle relative to the normal should a ray of light be directed upon the oil/glass interface such that it strikes the glass/air interface at the critical angle?arrow_forwardThe drawing shows a ray of light traveling from point A to point B, a distance of 9.10 m in a material than has an index of refraction n₁. At point B, the light encounters a different substance whose index of refraction is n₂ = 1.63. The light strikes the interface at the critical angle of 0c = 58.9°. How much time does it take for the light to travel from A to B? Number i n₂ = 1.63 n1 A Units >arrow_forward
- Problem 2: A beam of light traveling through a liquid (of index of refraction n1 = 1.31) is incident on a surface at an angle of θ1 = 55° with respect to the normal to the surface. It passes into the second medium and refracts at an angle of θ2 = 66.5° with respect to the normal. Part (a) Write an equation for the index of refraction of the second material. Part (b) What is the index of refraction of the second material? Part (c) Numerically, what is the light's velocity in medium 1, in meters per second? Part (d) Numerically, what is the light's velocity in medium 2, in meters per second?arrow_forwardA common trick in fiber optics is to send several colors of light down the same fiber (this is a form of what's called multiplexing). Each color of light can carry a separate signal, letting you squeeze more information into your beam. This, of course, leaves you with the problem of how to separate the colors back out once your beam gets to where its going. One way to do this involves total internal reflection.The index of refraction of glass isn't fixed; it's actually a function of frequency. Specifically, the index of the glass n and the angular frequency ω of the light are related by the equation below. Since different colors of light see different indices of refraction, different colors of light will see different critical angles.Suppose we have a beam with green light (frequency ω=3.7e+15 rad/s and red light (frequency ω=2.9e+15 rad/s traveling through this glass. Eventually, it's going to hit a glass-air boundary. At what angle of incidence θ should the light hit the boundary if…arrow_forwardA common trick in fiber optics is to send several colors of light down the same fiber (this is a form of what's called multiplexing). Each color of light can carry a separate signal, letting you squeeze more information into your beam. This, of course, leaves you with the problem of how to separate the colors back out once your beam gets to where its going. One way to do this involves total internal reflection.The index of refraction of glass isn't fixed; it's actually a function of frequency. Specifically, the index of the glass n and the angular frequency ω of the light are related by (see equation in image). Since different colors of light see different indices of refraction, different colors of light will see different critical angles.Suppose we have a beam with orange light (frequency ω=3.1e+15 rad/s and red light (frequency ω=2.9e+15 rad/s traveling through this glass. Eventually it's going to hit a glass-air boundary. At what angle of incidence θ should the light hit the…arrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
