College Algebra (Collegiate Math)
2nd Edition
ISBN: 9780077836344
Author: Julie Miller, Donna Gerken
Publisher: McGraw-Hill Education
expand_more
expand_more
format_list_bulleted
Videos
Question
Chapter 3.5, Problem 13PE
(a)
To determine
To fill: The blanks provided for the statement “In the given graph of a function, as
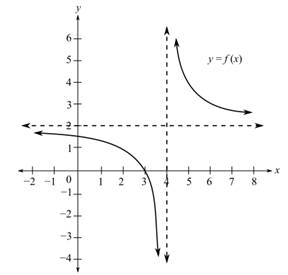
(b)
To determine
To fill: The blanks provided for the statement “In the given graph of a function, as
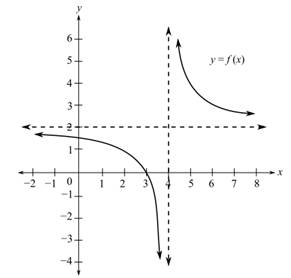
(c)
To determine
To fill: The blanks provided for the statement “In the given graph of a function, as
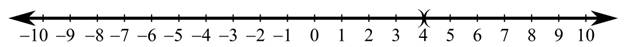
(d)
To determine
To fill: The blanks provided for the statement “In the given graph of a function, as
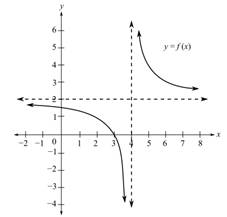
(e)
To determine
To fill: The blanks provided for the statement “The given graph of a function is increasing over the interval(s) _____________”
(f)
To determine
To fill: The blanks provided for the statement “The given graph of a function is decreasing over the interval(s) _____________”
(g)
To determine
To fill: The blanks provided for the statement “In the given graph of a function, the domain is _____________”
(h)
To determine
To fill: The blanks provided for the statement “In the given graph of a function, the range is _____________”
(i)
To determine
To fill: The blanks provided for the statement “In the given graph of a function, the vertical asymptote is the line _____________”
(j)
To determine
To fill: The blanks provided for the statement “In the given graph of a function, the horizontal asymptote is the line _____________”
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Describe the end behavior of the function f (æ) = -2x +3x2 – 5x + 1.
.f (x) →
as x →
.f (a) →
as x →
3R
Which graph represents the function y-2sin(x-x)+1?
A.
3n/2
3n/2
3n/2
21
3/2
2n
-2n
3n/2
B.
Chapter 3 Solutions
College Algebra (Collegiate Math)
Ch. 3.1 - Skill Practice 1
Repeat Example 1 with
Ch. 3.1 - Skill Practice 2 Repeat Example 2 with...Ch. 3.1 - Skill Practice 3 Repeat Example 3 with f(x)=x24x7.Ch. 3.1 - Skill Practice 4 A quarterback throws a football...Ch. 3.1 - Skill Practice 5
A farmer has 200 ft of fencing...Ch. 3.1 - Skill Practice 6 The funding f(t) (in $ millions)...Ch. 3.1 - 1. A function defined by is called a...Ch. 3.1 - Prob. 2PECh. 3.1 - Prob. 3PECh. 3.1 - Prob. 4PE
Ch. 3.1 - 5. Given if, the parabola opens (upward/downward)...Ch. 3.1 - Prob. 6PECh. 3.1 - For Exercises 7–14,
a. Determine whether the graph...Ch. 3.1 - For Exercises 714, a. Determine whether the graph...Ch. 3.1 - For Exercises 7–14,
a. Determine whether the graph...Ch. 3.1 - For Exercises 7–14,
a. Determine whether the graph...Ch. 3.1 - For Exercises 714, a. Determine whether the graph...Ch. 3.1 - For Exercises 714, a. Determine whether the graph...Ch. 3.1 - For Exercises 714, a. Determine whether the graph...Ch. 3.1 - Prob. 14PECh. 3.1 - For Exercises 15–24,
a. Write the function in...Ch. 3.1 - Prob. 16PECh. 3.1 - For Exercises 15–24,
a. Write the function in...Ch. 3.1 - For Exercises 1524, a. Write the function in...Ch. 3.1 - For Exercises 1524, a. Write the function in...Ch. 3.1 - For Exercises 15–24,
a. Write the function in...Ch. 3.1 - For Exercises 1524, a. Write the function in...Ch. 3.1 - Prob. 22PECh. 3.1 - For Exercises 1524, a. Write the function in...Ch. 3.1 - Prob. 24PECh. 3.1 - For Exercises 2532, find the vertex of the...Ch. 3.1 - Prob. 26PECh. 3.1 - For Exercises 2532, find the vertex of the...Ch. 3.1 - For Exercises 2532, find the vertex of the...Ch. 3.1 - For Exercises 25–32, find the vertex of the...Ch. 3.1 - For Exercises 25–32, find the vertex of the...Ch. 3.1 - For Exercises 25–32, find the vertex of the...Ch. 3.1 - For Exercises 2532, find the vertex of the...Ch. 3.1 - For Exercises 33–42,
a. State whether the graph of...Ch. 3.1 - For Exercises 33–42,
a. State whether the graph of...Ch. 3.1 - For Exercises 33–42,
a. State whether the graph of...Ch. 3.1 - For Exercises 3342, a. State whether the graph of...Ch. 3.1 - For Exercises 3342, a. State whether the graph of...Ch. 3.1 - For Exercises 33–42,
a. State whether the graph of...Ch. 3.1 - For Exercises 33–42,
a. State whether the graph of...Ch. 3.1 - For Exercises 3342, a. State whether the graph of...Ch. 3.1 - For Exercises 3342, a. State whether the graph of...Ch. 3.1 - For Exercises 3342, a. State whether the graph of...Ch. 3.1 - 43. The monthly profit for a small company that...Ch. 3.1 - 44. The monthly profit for a company that makes...Ch. 3.1 - A long jumper leaves the ground at an angle of 208...Ch. 3.1 - 46. A firefighter holds a hose 3 m off the ground...Ch. 3.1 - 47. The population of a culture of the bacterium...Ch. 3.1 - 48. The gas mileage m(x) (in mpg) for a certain...Ch. 3.1 - 49. The sum of two positive numbers is 24. What...Ch. 3.1 - Prob. 50PECh. 3.1 - Prob. 51PECh. 3.1 - Prob. 52PECh. 3.1 - Suppose that a family wants to fence in an area of...Ch. 3.1 - 54. Two chicken coops are to be built adjacent to...Ch. 3.1 - 55. A trough at the end of a gutter spout is meant...Ch. 3.1 - A rectangular frame of uniform depth for a shadow...Ch. 3.1 - Prob. 57PECh. 3.1 - Gas mileage is tested for a car under different...Ch. 3.1 - 59. Fluid runs through a drainage pipe with a...Ch. 3.1 - The braking distance required for a car to stop...Ch. 3.1 - Prob. 61PECh. 3.1 - For Exercises 6164, given a quadratic function...Ch. 3.1 - Prob. 63PECh. 3.1 - For Exercises 61–64, given a quadratic function...Ch. 3.1 - Prob. 65PECh. 3.1 - Prob. 66PECh. 3.1 - Prob. 67PECh. 3.1 - Prob. 68PECh. 3.1 - Prob. 69PECh. 3.1 - Prob. 70PECh. 3.1 - Prob. 71PECh. 3.1 - For Exercises 71–78, given a quadratic function...Ch. 3.1 - Prob. 73PECh. 3.1 - For Exercises 7178, given a quadratic function...Ch. 3.1 - Prob. 75PECh. 3.1 - Prob. 76PECh. 3.1 - For Exercises 71–78, given a quadratic function...Ch. 3.1 - For Exercises 7178, given a quadratic function...Ch. 3.1 - Prob. 79PECh. 3.1 - Prob. 80PECh. 3.1 - Prob. 81PECh. 3.1 - Prob. 82PECh. 3.1 - Prob. 83PECh. 3.1 - Prob. 84PECh. 3.1 - Prob. 85PECh. 3.1 - Prob. 86PECh. 3.1 - Prob. 87PECh. 3.1 - For Exercises 85 88, define a quadratic function...Ch. 3.1 - Prob. 89PECh. 3.1 - Prob. 90PECh. 3.1 - Prob. 91PECh. 3.1 - Prob. 92PECh. 3.2 - Skill Practice 1
Use the leading term to...Ch. 3.2 - Skill Practice 2 Find the zeros of the function...Ch. 3.2 - Skill Practice 3
Find the zeros of the function...Ch. 3.2 - Skill Practice 4 Use the leading term to determine...Ch. 3.2 - Skill Practice 5 Show that f(x)=x4+6x326x+15 has a...Ch. 3.2 - Skill Practice 6
Graph .
Ch. 3.2 - Skill Practice 7 Graph h(x)=05x(x1)(x+3)2.Ch. 3.2 - 1. A function defined by where are real...Ch. 3.2 - Prob. 2PECh. 3.2 - Prob. 3PECh. 3.2 - Prob. 4PECh. 3.2 - Prob. 5PECh. 3.2 - Prob. 6PECh. 3.2 - Prob. 7PECh. 3.2 - Prob. 8PECh. 3.2 - Prob. 9PECh. 3.2 - Prob. 10PECh. 3.2 - Prob. 11PECh. 3.2 - Prob. 12PECh. 3.2 - For Exercises 1320, determine the end behavior of...Ch. 3.2 - For Exercises 13–20, determine the end behavior of...Ch. 3.2 - For Exercises 1320, determine the end behavior of...Ch. 3.2 - Prob. 16PECh. 3.2 - For Exercises 13–20, determine the end behavior of...Ch. 3.2 - For Exercises 1320, determine the end behavior of...Ch. 3.2 - For Exercises 1320, determine the end behavior of...Ch. 3.2 - For Exercises 13–20, determine the end behavior of...Ch. 3.2 - Given the function defined by g(x)=3(x1)3(x+5)4,...Ch. 3.2 - Given the function defined by h(x)=12x5(x+0.6)3,...Ch. 3.2 - For Exercises 2338, find the zeros of the function...Ch. 3.2 - For Exercises 2338, find the zeros of the function...Ch. 3.2 - For Exercises 23–38, find the zeros of the...Ch. 3.2 - For Exercises 23–38, find the zeros of the...Ch. 3.2 - For Exercises 23–38, find the zeros of the...Ch. 3.2 - For Exercises 23–38, find the zeros of the...Ch. 3.2 - For Exercises 2338, find the zeros of the function...Ch. 3.2 - For Exercises 23–38, find the zeros of the...Ch. 3.2 - For Exercises 23–38, find the zeros of the...Ch. 3.2 - For Exercises 23–38, find the zeros of the...Ch. 3.2 - For Exercises 23–38, find the zeros of the...Ch. 3.2 - Prob. 34PECh. 3.2 - For Exercises 23–38, find the zeros of the...Ch. 3.2 - For Exercises 23–38, find the zeros of the...Ch. 3.2 - For Exercises 23–38, find the zeros of the...Ch. 3.2 - For Exercises 23–38, find the zeros of the...Ch. 3.2 - For Exercises 39–40, determine whether the...Ch. 3.2 - For Exercises 39–40, determine whether the...Ch. 3.2 - Prob. 41PECh. 3.2 - Prob. 42PECh. 3.2 - Prob. 43PECh. 3.2 - Prob. 44PECh. 3.2 - For Exercises 4552, determine if the graph can...Ch. 3.2 - Prob. 46PECh. 3.2 - For Exercises 4552, determine if the graph can...Ch. 3.2 - For Exercises 4552, determine if the graph can...Ch. 3.2 - Prob. 49PECh. 3.2 - Prob. 50PECh. 3.2 - Prob. 51PECh. 3.2 - Prob. 52PECh. 3.2 - For Exercises 5358, a. Identify the power function...Ch. 3.2 - Prob. 54PECh. 3.2 - For Exercises 5358, a. Identify the power function...Ch. 3.2 - Prob. 56PECh. 3.2 - For Exercises 5358, a. Identify the power function...Ch. 3.2 - Prob. 58PECh. 3.2 - For Exercises 59–76, sketch the function. (See...Ch. 3.2 - Prob. 60PECh. 3.2 - For Exercises 5976, sketch the function. (See...Ch. 3.2 - For Exercises 59–76, sketch the function. (See...Ch. 3.2 - For Exercises 5976, sketch the function. (See...Ch. 3.2 - Prob. 64PECh. 3.2 - For Exercises 59–76, sketch the function. (See...Ch. 3.2 - For Exercises 59–76, sketch the function. (See...Ch. 3.2 - For Exercises 59–76, sketch the function. (See...Ch. 3.2 - Prob. 68PECh. 3.2 - For Exercises 5976, sketch the function. (See...Ch. 3.2 - Prob. 70PECh. 3.2 - For Exercises 5976, sketch the function. (See...Ch. 3.2 - Prob. 72PECh. 3.2 - For Exercises 59–76, sketch the function. (See...Ch. 3.2 - Prob. 74PECh. 3.2 - For Exercises 5976, sketch the function. (See...Ch. 3.2 - Prob. 76PECh. 3.2 - Prob. 77PECh. 3.2 - For Exercises 77–88, determine if the statement is...Ch. 3.2 - For Exercises 77–88, determine if the statement is...Ch. 3.2 - For Exercises 7788, determine if the statement is...Ch. 3.2 - For Exercises 7788, determine if the statement is...Ch. 3.2 - Prob. 82PECh. 3.2 - Prob. 83PECh. 3.2 - Prob. 84PECh. 3.2 - Prob. 85PECh. 3.2 - Prob. 86PECh. 3.2 - Prob. 87PECh. 3.2 - For Exercises 7788, determine if the statement is...Ch. 3.2 - 89. A rocket will carry a communications satellite...Ch. 3.2 - 90. Data from a 20-yr study show the number of new...Ch. 3.2 - 91. Given a polynomial function defined by,...Ch. 3.2 - Write an informal explanation of what it means for...Ch. 3.2 - Prob. 93PECh. 3.2 - Prob. 94PECh. 3.2 - Prob. 95PECh. 3.2 - Prob. 96PECh. 3.2 - Prob. 97PECh. 3.2 - 98. The torque (in ft-lb) produced by a certain...Ch. 3.2 - Prob. 99PECh. 3.2 - Prob. 100PECh. 3.2 - Prob. 101PECh. 3.2 - Prob. 102PECh. 3.2 - For Exercises 102–103, graph the function defined...Ch. 3.3 - Skill Practice 1
Use long division to divide.
Ch. 3.3 - Skill Practice 2 Use long division to divide....Ch. 3.3 - Skill Practice 3
Use long division to divide.
Ch. 3.3 - Skill Practice 4
Use synthetic division to...Ch. 3.3 - Skill Practice 5
Use synthetic division to...Ch. 3.3 - Skill Practice 6
Given use the remainder theorem...Ch. 3.3 - Skill Practice 7
Use the remainder theorem to...Ch. 3.3 - Skill Practice 8
Use the factor theorem to...Ch. 3.3 - Skill Practice 9
a. Factor, given that –4 is a...Ch. 3.3 - Skill Practice 10 Write a polynomial f(x) of...Ch. 3.3 - Prob. 1PECh. 3.3 - Prob. 2PECh. 3.3 - Prob. 3PECh. 3.3 - Prob. 4PECh. 3.3 - Prob. 5PECh. 3.3 - Prob. 6PECh. 3.3 - Prob. 7PECh. 3.3 - For Exercises 7–8, (See Example 1)
a. Use long...Ch. 3.3 - For Exercises 922, use long division to divide,...Ch. 3.3 - For Exercises 922, use long division to divide,...Ch. 3.3 - For Exercises 922, use long division to divide,...Ch. 3.3 - For Exercises 9–22, use long division to divide,...Ch. 3.3 - For Exercises 922, use long division to divide,...Ch. 3.3 - For Exercises 922, use long division to divide,...Ch. 3.3 - For Exercises 922, use long division to divide,...Ch. 3.3 - For Exercises 922, use long division to divide,...Ch. 3.3 - For Exercises 9–22, use long division to divide,...Ch. 3.3 - Prob. 18PECh. 3.3 - For Exercises 922, use long division to divide,...Ch. 3.3 - For Exercises 9–22, use long division to divide,...Ch. 3.3 - For Exercises 9–22, use long division to divide,...Ch. 3.3 - For Exercises 9–22, use long division to divide,...Ch. 3.3 - For Exercises 2326, consider the division of two...Ch. 3.3 - Prob. 24PECh. 3.3 - For Exercises 2326, consider the division of two...Ch. 3.3 - Prob. 26PECh. 3.3 - For Exercises 27–38, use synthetic division to...Ch. 3.3 - For Exercises 2738, use synthetic division to...Ch. 3.3 - For Exercises 2738, use synthetic division to...Ch. 3.3 - Prob. 30PECh. 3.3 - For Exercises 27–38, use synthetic division to...Ch. 3.3 - Prob. 32PECh. 3.3 - For Exercises 27–38, use synthetic division to...Ch. 3.3 - Prob. 34PECh. 3.3 - For Exercises 2738, use synthetic division to...Ch. 3.3 - Prob. 36PECh. 3.3 - For Exercises 27–38, use synthetic division to...Ch. 3.3 - Prob. 38PECh. 3.3 - 39. The value for a polynomial. What can be...Ch. 3.3 - Prob. 40PECh. 3.3 - 41. Given.
a. Evaluate.
b. Determine the...Ch. 3.3 - Prob. 42PECh. 3.3 - For Exercises 4346, use the remainder theorem to...Ch. 3.3 - For Exercises 4346, use the remainder theorem to...Ch. 3.3 - For Exercises 43–46, use the remainder theorem to...Ch. 3.3 - Prob. 46PECh. 3.3 - For Exercises 4754, use the remainder theorem to...Ch. 3.3 - Prob. 48PECh. 3.3 - For Exercises 47–54, use the remainder theorem to...Ch. 3.3 - Prob. 50PECh. 3.3 - For Exercises 47–54, use the remainder theorem to...Ch. 3.3 - For Exercises 4754, use the remainder theorem to...Ch. 3.3 - For Exercises 47–54, use the remainder theorem to...Ch. 3.3 - Prob. 54PECh. 3.3 - For Exercises 55–60, use the factor theorem to...Ch. 3.3 - Prob. 56PECh. 3.3 - For Exercises 5560, use the factor theorem to...Ch. 3.3 - Prob. 58PECh. 3.3 - For Exercises 55–60, use the factor theorem to...Ch. 3.3 - Prob. 60PECh. 3.3 - 61. Given,
a. Evaluate.
b. Evaluate.
c. Solve....Ch. 3.3 - Prob. 62PECh. 3.3 - a. Use synthetic division and the factor theorem...Ch. 3.3 - Prob. 64PECh. 3.3 - a. Factor f(x)=2x2+x237x36, given that 1is a zero....Ch. 3.3 - Prob. 66PECh. 3.3 - 67. a. Factor is a zero.
b. Solve.
Ch. 3.3 - 68. a. Factor is a zero.
b. Solve.
Ch. 3.3 - 69. a. Factor, given that 3 is a zero.
b. Solve....Ch. 3.3 - Prob. 70PECh. 3.3 - For Exercises 7182, write a polynomial f(x) that...Ch. 3.3 - Prob. 72PECh. 3.3 - For Exercises 7182, write a polynomial f(x) that...Ch. 3.3 - Prob. 74PECh. 3.3 - For Exercises 7182, write a polynomial f(x) that...Ch. 3.3 - Prob. 76PECh. 3.3 - For Exercises 71–82, write a polynomial that meets...Ch. 3.3 - Prob. 78PECh. 3.3 - For Exercises 7182, write a polynomial f(x) that...Ch. 3.3 - Prob. 80PECh. 3.3 - For Exercises 7182, write a polynomial f(x) that...Ch. 3.3 - Prob. 82PECh. 3.3 - Prob. 83PECh. 3.3 - Prob. 84PECh. 3.3 - Prob. 85PECh. 3.3 - Prob. 86PECh. 3.3 - Prob. 87PECh. 3.3 - Prob. 88PECh. 3.3 - Prob. 89PECh. 3.3 - Prob. 90PECh. 3.3 - Prob. 91PECh. 3.3 - Prob. 92PECh. 3.3 - Prob. 93PECh. 3.3 - Prob. 94PECh. 3.3 - Prob. 95PECh. 3.3 - Prob. 96PECh. 3.3 - Prob. 97PECh. 3.3 - How can the division algorithm be used to check...Ch. 3.3 - Prob. 99PECh. 3.3 - Prob. 100PECh. 3.3 - Prob. 101PECh. 3.3 - Prob. 102PECh. 3.3 - Prob. 103PECh. 3.3 - Prob. 104PECh. 3.3 - Prob. 105PECh. 3.3 - Prob. 106PECh. 3.4 - Skill Practice 1 List all possible rational zeros....Ch. 3.4 - Skill Practice 2 Find the zeros. f(x)=x3x24x2Ch. 3.4 - Skill Practice 3
Find the zeros and their...Ch. 3.4 - Skill Practice 4
Find the zeros.
Ch. 3.4 - Skill Practice 5
Given, and that is a zero of.
a....Ch. 3.4 - Skill Practice 6
a. Find a third-degree...Ch. 3.4 - Skill Practice 7 Determine the number of possible...Ch. 3.4 - Skill Practice 8
Determine the number of possible...Ch. 3.4 - Skill Practice 9 Given f(x)=x42x313x24x30. a....Ch. 3.4 - Skill Practice 10
Find the zeros and their...Ch. 3.4 - Prob. 1PECh. 3.4 - If f(x) is a polynomial of degree n1 with complex...Ch. 3.4 - Prob. 3PECh. 3.4 - A real number b is called an __________ bound of...Ch. 3.4 - Prob. 5PECh. 3.4 - Prob. 6PECh. 3.4 - For Exercises 7–12, list the possible rational...Ch. 3.4 - For Exercises 712, list the possible rational...Ch. 3.4 - For Exercises 7–12, list the possible rational...Ch. 3.4 - Prob. 10PECh. 3.4 - For Exercises 712, list the possible rational...Ch. 3.4 - For Exercises 712, list the possible rational...Ch. 3.4 - Which of the following is not a possible zero of...Ch. 3.4 - 14. Which of the following is not a possible zero...Ch. 3.4 - For Exercises 15–16, find all the rational zeros....Ch. 3.4 - For Exercises 15–16, find all the rational zeros....Ch. 3.4 - For Exercises 17–28, find all the zeros. (See...Ch. 3.4 - Prob. 18PECh. 3.4 - For Exercises 1728, find all the zeros. (See...Ch. 3.4 - For Exercises 1728, find all the zeros. (See...Ch. 3.4 - For Exercises 17–28, find all the zeros. (See...Ch. 3.4 - For Exercises 17–28, find all the zeros. (See...Ch. 3.4 - For Exercises 1728, find all the zeros. (See...Ch. 3.4 - Prob. 24PECh. 3.4 - For Exercises 1728, find all the zeros. (See...Ch. 3.4 - Prob. 26PECh. 3.4 - For Exercises 17–28, find all the zeros. (See...Ch. 3.4 - Prob. 28PECh. 3.4 - Prob. 29PECh. 3.4 - Prob. 30PECh. 3.4 - If f(x) is a polynomial with real coefficients and...Ch. 3.4 - Prob. 32PECh. 3.4 - Prob. 33PECh. 3.4 - Prob. 34PECh. 3.4 - For Exercises 3338, a polynomial f(x) and one or...Ch. 3.4 - Prob. 36PECh. 3.4 - For Exercises 33–38, a polynomial and one or more...Ch. 3.4 - Prob. 38PECh. 3.4 - For Exercises 39–48, write a polynomial that...Ch. 3.4 - For Exercises 39–48, write a polynomial that...Ch. 3.4 - For Exercises 39–48, write a polynomial that...Ch. 3.4 - For Exercises 3948, write a polynomial f(x) that...Ch. 3.4 - For Exercises 3948, write a polynomial f(x) that...Ch. 3.4 - For Exercises 3948, write a polynomial f(x) that...Ch. 3.4 - For Exercises 3948, write a polynomial f(x) that...Ch. 3.4 - Prob. 46PECh. 3.4 - For Exercises 3948, write a polynomial f(x) that...Ch. 3.4 - Prob. 48PECh. 3.4 - Prob. 49PECh. 3.4 - Prob. 50PECh. 3.4 - Prob. 51PECh. 3.4 - Prob. 52PECh. 3.4 - Prob. 53PECh. 3.4 - Prob. 54PECh. 3.4 - Prob. 55PECh. 3.4 - Prob. 56PECh. 3.4 - Prob. 57PECh. 3.4 - Prob. 58PECh. 3.4 - Prob. 59PECh. 3.4 - Prob. 60PECh. 3.4 - Prob. 61PECh. 3.4 - For Exercises 59–64, (See Example 9)
a. Determine...Ch. 3.4 - Prob. 63PECh. 3.4 - Prob. 64PECh. 3.4 - Prob. 65PECh. 3.4 - Prob. 66PECh. 3.4 - Prob. 67PECh. 3.4 - For Exercises 65–68, determine if the statement is...Ch. 3.4 - Prob. 69PECh. 3.4 - Prob. 70PECh. 3.4 - Prob. 71PECh. 3.4 - Fir Exercises 69–84, find the zeros and their...Ch. 3.4 - Prob. 73PECh. 3.4 - Fir Exercises 6984, find the zeros and their...Ch. 3.4 - Prob. 75PECh. 3.4 - Prob. 76PECh. 3.4 - Prob. 77PECh. 3.4 - Prob. 78PECh. 3.4 - Prob. 79PECh. 3.4 - Fir Exercises 69–84, find the zeros and their...Ch. 3.4 - Prob. 81PECh. 3.4 - Prob. 82PECh. 3.4 - Fir Exercises 6984, find the zeros and their...Ch. 3.4 - Prob. 84PECh. 3.4 - Prob. 85PECh. 3.4 - Prob. 86PECh. 3.4 - Prob. 87PECh. 3.4 - Prob. 88PECh. 3.4 - Prob. 89PECh. 3.4 - Prob. 90PECh. 3.4 - Prob. 91PECh. 3.4 - Prob. 92PECh. 3.4 - Prob. 93PECh. 3.4 - Prob. 94PECh. 3.4 - Prob. 95PECh. 3.4 - Prob. 96PECh. 3.4 - Prob. 97PECh. 3.4 - Prob. 98PECh. 3.4 - Prob. 99PECh. 3.4 - Prob. 100PECh. 3.4 - The front face of a tent is triangular and the...Ch. 3.4 - Prob. 102PECh. 3.4 - Prob. 103PECh. 3.4 - Prob. 104PECh. 3.4 - Prob. 105PECh. 3.4 - Prob. 106PECh. 3.4 - Prob. 107PECh. 3.4 - Prob. 108PECh. 3.4 - Prob. 109PECh. 3.4 - Prob. 110PECh. 3.4 - Prob. 111PECh. 3.4 - Find all sixth roots of 1, by solving the equation...Ch. 3.4 - Use the rational zero theorem to show that 5 is an...Ch. 3.4 - Prob. 114PECh. 3.4 - Prob. 115PECh. 3.4 - Foe Exercises 115116, use the formula...Ch. 3.5 - Skill Practice 1
The graph of is given.
a. As...Ch. 3.5 - Skill Practice 2
Identify the vertical...Ch. 3.5 - Skill Practice 3
Find the horizontal asymptotes...Ch. 3.5 - Skill Practice 4 Given g(x)=3x2+4x3x2+3, determine...Ch. 3.5 - Skill Practice 5
Determine the asymptotes.
Ch. 3.5 - Skill Practice 6
Use transformations to graph.
Ch. 3.5 - Skill Practice 7 Graph f(x)=x1x+4.Ch. 3.5 - Skill Practice 8 Graph g(x)=5xx29.Ch. 3.5 - Skill Practice 9 Graph g(x)=4x2+7x2x2+4.Ch. 3.5 - Skill Practice 10 Graph k(x)=2x27x+3x2.Ch. 3.5 - Skill Practice 11
Repeat Example 11 under the...Ch. 3.5 - Prob. 1PECh. 3.5 - 2. The notation is read as _________.
Ch. 3.5 - Prob. 3PECh. 3.5 - Prob. 4PECh. 3.5 - Prob. 5PECh. 3.5 - Prob. 6PECh. 3.5 - For Exercises 712, write the domain of the...Ch. 3.5 - For Exercises 712, write the domain of the...Ch. 3.5 - For Exercises 7–12, write the domain of the...Ch. 3.5 - For Exercises 712, write the domain of the...Ch. 3.5 - For Exercises 7–12, write the domain of the...Ch. 3.5 - Prob. 12PECh. 3.5 - Prob. 13PECh. 3.5 - Prob. 14PECh. 3.5 - Prob. 15PECh. 3.5 - For Exercises 1316, refer to the graph of the...Ch. 3.5 - For Exercises 17–24, determine the vertical...Ch. 3.5 - For Exercises 1724, determine the vertical...Ch. 3.5 - For Exercises 1724, determine the vertical...Ch. 3.5 - For Exercises 1724, determine the vertical...Ch. 3.5 - For Exercises 17–24, determine the vertical...Ch. 3.5 - For Exercises 17–24, determine the vertical...Ch. 3.5 - For Exercises 1724, determine the vertical...Ch. 3.5 - Prob. 24PECh. 3.5 - 25. The graph of will behave like which function...Ch. 3.5 - Prob. 26PECh. 3.5 - 27. The graph of will behave like which function...Ch. 3.5 - Prob. 28PECh. 3.5 - For Exercises 2936, a. Identify the horizontal...Ch. 3.5 - Prob. 30PECh. 3.5 - For Exercises 29–36,
a. Identify the horizontal...Ch. 3.5 - For Exercises 2936, a. Identify the horizontal...Ch. 3.5 - For Exercises 2936, a. Identify the horizontal...Ch. 3.5 - Prob. 34PECh. 3.5 - For Exercises 29–36,
a. Identify the horizontal...Ch. 3.5 - Prob. 36PECh. 3.5 - Prob. 37PECh. 3.5 - Prob. 38PECh. 3.5 - For Exercises 39–48, identify the asymptotes. (See...Ch. 3.5 - For Exercises 3948, identify the asymptotes. (See...Ch. 3.5 - For Exercises 3948, identify the asymptotes. (See...Ch. 3.5 - For Exercises 3948, identify the asymptotes. (See...Ch. 3.5 - For Exercises 39–48, identify the asymptotes. (See...Ch. 3.5 - For Exercises 3948, identify the asymptotes. (See...Ch. 3.5 - For Exercises 3948, identify the asymptotes. (See...Ch. 3.5 - Prob. 46PECh. 3.5 - Prob. 47PECh. 3.5 - Prob. 48PECh. 3.5 - Prob. 49PECh. 3.5 - Prob. 50PECh. 3.5 - Prob. 51PECh. 3.5 - Prob. 52PECh. 3.5 - Prob. 53PECh. 3.5 - Prob. 54PECh. 3.5 - Prob. 55PECh. 3.5 - Prob. 56PECh. 3.5 - Prob. 57PECh. 3.5 - For Exercises 5762, for the graph of y=f(x). a....Ch. 3.5 - For Exercises 5762, for the graph of y=f(x). a....Ch. 3.5 - Prob. 60PECh. 3.5 - Prob. 61PECh. 3.5 - For Exercises 57–62, for the graph...Ch. 3.5 - Prob. 63PECh. 3.5 - Prob. 64PECh. 3.5 - Prob. 65PECh. 3.5 - Prob. 66PECh. 3.5 - For Exercises 6790, graph the function. (See...Ch. 3.5 - Prob. 68PECh. 3.5 - For Exercises 67–90, graph the function. (See...Ch. 3.5 - Prob. 70PECh. 3.5 - For Exercises 6790, graph the function. (See...Ch. 3.5 - Prob. 72PECh. 3.5 - For Exercises 6790, graph the function. (See...Ch. 3.5 - Prob. 74PECh. 3.5 - For Exercises 6790, graph the function. (See...Ch. 3.5 - For Exercises 67–90, graph the function. (See...Ch. 3.5 - For Exercises 6790, graph the function. (See...Ch. 3.5 - Prob. 78PECh. 3.5 - For Exercises 6790, graph the function. (See...Ch. 3.5 - Prob. 80PECh. 3.5 - For Exercises 6790, graph the function. (See...Ch. 3.5 - For Exercises 67–90, graph the function. (See...Ch. 3.5 - For Exercises 67–90, graph the function. (See...Ch. 3.5 - Prob. 84PECh. 3.5 - For Exercises 67–90, graph the function. (See...Ch. 3.5 - Prob. 86PECh. 3.5 - For Exercises 6790, graph the function. (See...Ch. 3.5 - Prob. 88PECh. 3.5 - Prob. 89PECh. 3.5 - Prob. 90PECh. 3.5 - 91. A sports trainer has monthly costs of $69.95...Ch. 3.5 - Prob. 92PECh. 3.5 - Prob. 93PECh. 3.5 - Prob. 94PECh. 3.5 - Prob. 95PECh. 3.5 - A certain diet pill is designed to delay the...Ch. 3.5 - Prob. 97PECh. 3.5 - 98. The cost (in $1000) for a city to remove x%...Ch. 3.5 - The Doppler effect is a change in the observed...Ch. 3.5 - The Doppler effect is a change in the observed...Ch. 3.5 - Prob. 101PECh. 3.5 - Prob. 102PECh. 3.5 - Prob. 103PECh. 3.5 - Prob. 104PECh. 3.5 - Prob. 105PECh. 3.5 - Prob. 106PECh. 3.5 - Prob. 107PECh. 3.5 - Prob. 108PECh. 3.5 - Prob. 109PECh. 3.5 - Prob. 110PECh. 3.5 - The rational functions studied in this section all...Ch. 3.5 - The rational functions studied in this section all...Ch. 3.5 - The rational functions studied in this section all...Ch. 3.5 - Prob. 114PECh. 3.5 - Prob. 1PRECh. 3.5 - Prob. 2PRECh. 3.5 - Prob. 3PRECh. 3.5 - Prob. 4PRECh. 3.5 - Prob. 5PRECh. 3.5 - Prob. 6PRECh. 3.5 - Prob. 7PRECh. 3.5 - Prob. 8PRECh. 3.5 - Prob. 9PRECh. 3.5 - Prob. 10PRECh. 3.5 - Prob. 11PRECh. 3.5 - For Exercises 916, refer to...Ch. 3.5 - Prob. 13PRECh. 3.5 - Prob. 14PRECh. 3.5 - Prob. 15PRECh. 3.5 - Prob. 16PRECh. 3.5 - Prob. 17PRECh. 3.5 - Prob. 18PRECh. 3.5 - Prob. 19PRECh. 3.5 - Prob. 20PRECh. 3.5 - Prob. 21PRECh. 3.5 - Prob. 22PRECh. 3.6 - Skill Practice 1
Solve the inequality.
Ch. 3.6 - Skill Practice 2 Solve the inequality. x418x3x24x3Ch. 3.6 - Prob. 3SPCh. 3.6 - Skill Practice 4
Solve the inequality.
Ch. 3.6 - Skill Practice 5
Solve the inequality.
Ch. 3.6 - Skill Practice 6
Solve the inequalities.
a. ...Ch. 3.6 - Skill Practice 7 Repeat Example 7 under the...Ch. 3.6 - 1. Let be a polynomial. An inequality of the form ...Ch. 3.6 - Prob. 2PECh. 3.6 - Prob. 3PECh. 3.6 - Prob. 4PECh. 3.6 - Prob. 5PECh. 3.6 - For Exercises 514, the graph of y=f(x) is given....Ch. 3.6 - Prob. 7PECh. 3.6 - For Exercises 514, the graph of y=f(x) is given....Ch. 3.6 - Prob. 9PECh. 3.6 - For Exercises 5–14, the graph of is given. Solve...Ch. 3.6 - Prob. 11PECh. 3.6 - For Exercises 514, the graph of y=f(x) is given....Ch. 3.6 - Prob. 13PECh. 3.6 - Prob. 14PECh. 3.6 - Prob. 15PECh. 3.6 - Prob. 16PECh. 3.6 - For Exercises 1520, solve the equations and...Ch. 3.6 - For Exercises 15–20, solve the equations and...Ch. 3.6 - For Exercises 15–20, solve the equations and...Ch. 3.6 - Prob. 20PECh. 3.6 - For Exercises 21–54, solve the inequalities. (See...Ch. 3.6 - Prob. 22PECh. 3.6 - For Exercises 2154, solve the inequalities. (See...Ch. 3.6 - Prob. 24PECh. 3.6 - For Exercises 21–54, solve the inequalities. (See...Ch. 3.6 - Prob. 26PECh. 3.6 - For Exercises 21–54, solve the inequalities. (See...Ch. 3.6 - Prob. 28PECh. 3.6 - For Exercises 21–54, solve the inequalities. (See...Ch. 3.6 - Prob. 30PECh. 3.6 - For Exercises 2154, solve the inequalities. (See...Ch. 3.6 - For Exercises 2154, solve the inequalities. (See...Ch. 3.6 - For Exercises 2154, solve the inequalities. (See...Ch. 3.6 - For Exercises 2154, solve the inequalities. (See...Ch. 3.6 - For Exercises 2154, solve the inequalities. (See...Ch. 3.6 - Prob. 36PECh. 3.6 - For Exercises 21–54, solve the inequalities. (See...Ch. 3.6 - Prob. 38PECh. 3.6 - For Exercises 2154, solve the inequalities. (See...Ch. 3.6 - Prob. 40PECh. 3.6 - For Exercises 21–54, solve the inequalities. (See...Ch. 3.6 - For Exercises 2154, solve the inequalities. (See...Ch. 3.6 - For Exercises 21–54, solve the inequalities. (See...Ch. 3.6 - Prob. 44PECh. 3.6 - For Exercises 2154, solve the inequalities. (See...Ch. 3.6 - Prob. 46PECh. 3.6 - For Exercises 21–54, solve the inequalities. (See...Ch. 3.6 - For Exercises 21–54, solve the inequalities. (See...Ch. 3.6 - For Exercises 21–54, solve the inequalities. (See...Ch. 3.6 - Prob. 50PECh. 3.6 - For Exercises 21–54, solve the inequalities. (See...Ch. 3.6 - Prob. 52PECh. 3.6 - For Exercises 21–54, solve the inequalities. (See...Ch. 3.6 - Prob. 54PECh. 3.6 - Prob. 55PECh. 3.6 - Prob. 56PECh. 3.6 - Prob. 57PECh. 3.6 - Prob. 58PECh. 3.6 - For Exercises 5962, solve the inequalities. (See...Ch. 3.6 - Prob. 60PECh. 3.6 - For Exercises 5962, solve the inequalities. (See...Ch. 3.6 - Prob. 62PECh. 3.6 - For Exercises 6384, solve the inequalities. (See...Ch. 3.6 - Prob. 64PECh. 3.6 - For Exercises 63–84, solve the inequalities. (See...Ch. 3.6 - Prob. 66PECh. 3.6 - For Exercises 63–84, solve the inequalities. (See...Ch. 3.6 - Prob. 68PECh. 3.6 - For Exercises 6384, solve the inequalities. (See...Ch. 3.6 - Prob. 70PECh. 3.6 - For Exercises 6384, solve the inequalities. (See...Ch. 3.6 - Prob. 72PECh. 3.6 - For Exercises 6384, solve the inequalities. (See...Ch. 3.6 - Prob. 74PECh. 3.6 - For Exercises 6384, solve the inequalities. (See...Ch. 3.6 - Prob. 76PECh. 3.6 - For Exercises 6384, solve the inequalities. (See...Ch. 3.6 - Prob. 78PECh. 3.6 - For Exercises 6384, solve the inequalities. (See...Ch. 3.6 - Prob. 80PECh. 3.6 - For Exercises 6384, solve the inequalities. (See...Ch. 3.6 - Prob. 82PECh. 3.6 - For Exercises 63–84, solve the inequalities. (See...Ch. 3.6 - Prob. 84PECh. 3.6 - Prob. 85PECh. 3.6 - 86. Suppose that a basketball player jumps...Ch. 3.6 - Prob. 87PECh. 3.6 - 88. The population of a bacteria culture is given...Ch. 3.6 - 89. Suppose that an object that is originally at...Ch. 3.6 - The average round trip speed S (in mph) of a...Ch. 3.6 - 91. A rectangular quilt is to be made so that the...Ch. 3.6 - A landscaping team plans to build a rectangular...Ch. 3.6 - Prob. 93PECh. 3.6 - Prob. 94PECh. 3.6 - Prob. 95PECh. 3.6 - Prob. 96PECh. 3.6 - Prob. 97PECh. 3.6 - Prob. 98PECh. 3.6 - Prob. 99PECh. 3.6 - Prob. 100PECh. 3.6 - Prob. 101PECh. 3.6 - Prob. 102PECh. 3.6 - Prob. 103PECh. 3.6 - Prob. 104PECh. 3.6 - Prob. 105PECh. 3.6 - Prob. 106PECh. 3.6 - Prob. 107PECh. 3.6 - Prob. 108PECh. 3.6 - The procedure to solve a polynomial or rational...Ch. 3.6 - The procedure to solve a polynomial or rational...Ch. 3.6 - The procedure to solve a polynomial or rational...Ch. 3.6 - The procedure to solve a polynomial or rational...Ch. 3.6 - The procedure to solve a polynomial or rational...Ch. 3.6 - Prob. 114PECh. 3.6 - Prob. 115PECh. 3.6 - Prob. 116PECh. 3.6 - Prob. 117PECh. 3.6 - The procedure to solve a polynomial or rational...Ch. 3.6 - Prob. 119PECh. 3.6 - Prob. 120PECh. 3.6 - Prob. 121PECh. 3.6 - Prob. 122PECh. 3.6 - Prob. 123PECh. 3.6 - 124. The concentration of a drug in the...Ch. 3.6 - Prob. 1PRECh. 3.6 - Prob. 2PRECh. 3.6 - Prob. 3PRECh. 3.6 - Prob. 4PRECh. 3.6 - Prob. 5PRECh. 3.6 - Prob. 6PRECh. 3.6 - Prob. 7PRECh. 3.6 - Prob. 8PRECh. 3.6 - Prob. 9PRECh. 3.6 - Prob. 10PRECh. 3.6 - Prob. 11PRECh. 3.6 - Prob. 12PRECh. 3.6 - Prob. 13PRECh. 3.6 - Prob. 14PRECh. 3.6 - Prob. 15PRECh. 3.6 - Prob. 16PRECh. 3.6 - Prob. 17PRECh. 3.6 - Prob. 18PRECh. 3.6 - Prob. 19PRECh. 3.6 - Prob. 20PRECh. 3.6 - Prob. 21PRECh. 3.6 - Prob. 22PRECh. 3.6 - Prob. 23PRECh. 3.6 - Prob. 24PRECh. 3.6 - Prob. 25PRECh. 3.6 - Prob. 26PRECh. 3.6 - Prob. 27PRECh. 3.6 - Prob. 28PRECh. 3.6 - Prob. 29PRECh. 3.6 - At this point in the text, we have studied several...Ch. 3.7 - Skill Practice 1 Write a variation model using k...Ch. 3.7 - Prob. 2SPCh. 3.7 - Skill Practice 3 The amount of the medicine...Ch. 3.7 - Prob. 4SPCh. 3.7 - Prob. 5SPCh. 3.7 - Prob. 1PECh. 3.7 - Prob. 2PECh. 3.7 - Prob. 3PECh. 3.7 - Prob. 4PECh. 3.7 - Prob. 5PECh. 3.7 - Prob. 6PECh. 3.7 - Prob. 7PECh. 3.7 - Prob. 8PECh. 3.7 - Prob. 9PECh. 3.7 - Prob. 10PECh. 3.7 - Prob. 11PECh. 3.7 - For Exercises 11–20, write a variation model using...Ch. 3.7 - Prob. 13PECh. 3.7 - Prob. 14PECh. 3.7 - For Exercises 11–20, write a variation model using...Ch. 3.7 - Prob. 16PECh. 3.7 - Prob. 17PECh. 3.7 - Prob. 18PECh. 3.7 - Prob. 19PECh. 3.7 - For Exercises 11–20, write a variation model using...Ch. 3.7 - Prob. 21PECh. 3.7 - Prob. 22PECh. 3.7 - For Exercises 21–26, find the constant of...Ch. 3.7 - Prob. 24PECh. 3.7 - Prob. 25PECh. 3.7 - Prob. 26PECh. 3.7 - Prob. 27PECh. 3.7 - Prob. 28PECh. 3.7 - Prob. 29PECh. 3.7 - Prob. 30PECh. 3.7 - Prob. 31PECh. 3.7 - Prob. 32PECh. 3.7 - For Exercises 2948, use a variation model to solve...Ch. 3.7 - Prob. 34PECh. 3.7 - Prob. 35PECh. 3.7 - Prob. 36PECh. 3.7 - For Exercises 29–48, use a variation model to...Ch. 3.7 - Prob. 38PECh. 3.7 - Prob. 39PECh. 3.7 - For Exercises 29–48, use a variation model to...Ch. 3.7 - Prob. 41PECh. 3.7 - Prob. 42PECh. 3.7 - Prob. 43PECh. 3.7 - Prob. 44PECh. 3.7 - Prob. 45PECh. 3.7 - For Exercises 2948, use a variation model to solve...Ch. 3.7 - Prob. 47PECh. 3.7 - For Exercises 29–48, use a variation model to...Ch. 3.7 - Prob. 49PECh. 3.7 - Prob. 50PECh. 3.7 - Prob. 51PECh. 3.7 - Prob. 52PECh. 3.7 - 53. Which formula (s) can represent a variation...Ch. 3.7 - Prob. 54PECh. 3.7 - Prob. 55PECh. 3.7 - Prob. 56PECh. 3.7 - Prob. 57PECh. 3.7 - Prob. 58PECh. 3.7 - Prob. 59PECh. 3.7 - Prob. 60PECh. 3.7 - Prob. 61PECh. 3.7 - Prob. 62PECh. 3.7 - Prob. 63PECh. 3.7 - Prob. 64PECh. 3 - Given f(x)=(x+5)2+2, identify the vertex of the...Ch. 3 - For Exercises 2–3,
a. Write the equation in...Ch. 3 - Prob. 3RECh. 3 - Prob. 4RECh. 3 - Prob. 5RECh. 3 - Suppose that p is the probability that a randomly...Ch. 3 - Prob. 7RECh. 3 - Prob. 8RECh. 3 - Prob. 9RECh. 3 - Prob. 10RECh. 3 - For Exercises 8–11,
a. Determine the end behavior...Ch. 3 - 12. Determine whether the intermediate value...Ch. 3 - Prob. 13RECh. 3 - For Exercises 1316, determine if the statement is...Ch. 3 - For Exercises 13–16, determine if the statement is...Ch. 3 - Prob. 16RECh. 3 - Prob. 17RECh. 3 - Prob. 18RECh. 3 - Prob. 19RECh. 3 - Prob. 20RECh. 3 - Prob. 21RECh. 3 - Prob. 22RECh. 3 - Prob. 23RECh. 3 - Prob. 24RECh. 3 - Prob. 25RECh. 3 - Prob. 26RECh. 3 - Prob. 27RECh. 3 - Prob. 28RECh. 3 - Prob. 29RECh. 3 - Prob. 30RECh. 3 - Prob. 31RECh. 3 - Prob. 32RECh. 3 - Prob. 33RECh. 3 - Prob. 34RECh. 3 - Prob. 35RECh. 3 - Prob. 36RECh. 3 - Prob. 37RECh. 3 - Prob. 38RECh. 3 - Prob. 39RECh. 3 - Prob. 40RECh. 3 - Prob. 41RECh. 3 - Prob. 42RECh. 3 - Prob. 43RECh. 3 - Prob. 44RECh. 3 - Prob. 45RECh. 3 - Prob. 46RECh. 3 - Prob. 47RECh. 3 - For Exercises 4851, graph the function. f(x)=1x4+2Ch. 3 - For Exercises 4851, graph the function....Ch. 3 - Prob. 50RECh. 3 - For Exercises 48–51, graph the function.
51.
Ch. 3 - After taking a certain class. The percentage of...Ch. 3 - Prob. 53RECh. 3 - Prob. 54RECh. 3 - Prob. 55RECh. 3 - Prob. 56RECh. 3 - Prob. 57RECh. 3 - Prob. 58RECh. 3 - Prob. 59RECh. 3 - Prob. 60RECh. 3 - Prob. 61RECh. 3 - Prob. 62RECh. 3 - Prob. 63RECh. 3 - Prob. 64RECh. 3 - Prob. 65RECh. 3 - Prob. 66RECh. 3 - 67. A sports trainer has monthly casts of $80 for...Ch. 3 - A child throws a ball straight upwards to his...Ch. 3 - Prob. 69RECh. 3 -
For Exercises 69–71, write a variation model...Ch. 3 - Prob. 71RECh. 3 - Prob. 72RECh. 3 - Prob. 73RECh. 3 - Prob. 74RECh. 3 - Prob. 75RECh. 3 - Prob. 76RECh. 3 - Prob. 77RECh. 3 - 1. Given.
a. Write the equation in vertex form:...Ch. 3 - Prob. 2TCh. 3 - Prob. 3TCh. 3 - Prob. 4TCh. 3 - Prob. 5TCh. 3 - Prob. 6TCh. 3 - Prob. 7TCh. 3 - Given f(x)=x48x3+21x232x+68 and that 2i is a zero...Ch. 3 - Given f(x)=3x4+7x312x214x+12, a. How many zeros...Ch. 3 - Prob. 10TCh. 3 - Determine the number of possible positive and...Ch. 3 - Prob. 12TCh. 3 - Prob. 13TCh. 3 - For Exercises 12–14, determine the asymptotes...Ch. 3 - Prob. 15TCh. 3 - Prob. 16TCh. 3 - For Exercises 15–17, graph the function,
17.
Ch. 3 - Prob. 18TCh. 3 - Prob. 19TCh. 3 - Prob. 20TCh. 3 - Prob. 21TCh. 3 - Prob. 22TCh. 3 - Prob. 23TCh. 3 - Prob. 24TCh. 3 - Prob. 25TCh. 3 - Prob. 26TCh. 3 - Prob. 27TCh. 3 - The weight of a body varies inversely as the...Ch. 3 - Prob. 29TCh. 3 - Prob. 30TCh. 3 - Prob. 31TCh. 3 - Suppose that a rocket is shot straight upward from...Ch. 3 - 33. The number of yearly visits to physicians’...Ch. 3 - Given r(x)=2x23x216, a. Find the vertical...Ch. 3 - Find a polynomial f(x) of lowest degree with real...Ch. 3 - Given f(x)=2x3x28x5, a. Determine the end behavior...Ch. 3 - 4. Divide and write the answer in the form
Ch. 3 - Prob. 5CRECh. 3 - 6. Determine an equation of the line passing...Ch. 3 - Prob. 7CRECh. 3 - Graph f(x)={x1forx1x1forx1Ch. 3 - Prob. 9CRECh. 3 - 10. Given,
a. Find the x-intercepts.
b. Find the...Ch. 3 - Prob. 11CRECh. 3 - For Exercises 1214, simplify the expression....Ch. 3 - Prob. 13CRECh. 3 - Prob. 14CRECh. 3 - Prob. 15CRECh. 3 - Prob. 16CRECh. 3 - Prob. 17CRECh. 3 - Prob. 18CRECh. 3 - Prob. 19CRECh. 3 - Prob. 20CRE
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.Similar questions
- 4. List the zero(s) of the following function: zero(s):arrow_forwardFor Exercises 93–102, write the domain of the function in interval notation. VI - P 93. f(x) = V9 - ? 95. h(a) = Va² – 5 94. g(t) = 96. f(u) = Vu? – 7 97. p(x) = V2x? + 9x – 18 98. q(x) = V4x² + 7x – 2 - 1 1 99. r(x) 100. s(x) V2r + 9x – 18 V4x + 7x – 2 - 3x 2x 101. h(x) = 102. k(x) = Vx + 2 Vx + 1arrow_forwardFor Exercises 9–18, graph the functions by plotting points or by using a graphing utility. Explain how the graphs are related. 9. a. f(x) = x b. g(x) = x + 2 c. h(x) = x² – 4 13. a. f(x) = |x| b. g(x) = -|x| 16. a. f(x) = |x| 1 b. g(x) = x| 14. a. f(x) = Vĩ b. g(x) = - Vĩ c. h(x) = 3|x| 10. a. f(x) = |x| b. g(x) = |x|+ 2 c. h(x) = |x| – 4 17. a. f(x) = V b. g(x) = V-x 15. a. f(x) = ? %3D b. g(x) = 11. a. f(x) = Vx b. g(x) = Vx – 2 c. h(x) = Vx + 4 18. a. f(x) = VI b. g(x) = V-x c. h(x) = 2r 12. a. f(x) = x b. g(x) = (x – 2)? c. h(x) = (x + 3)?arrow_forward
- 4. Find the equation of the function below! $ Carrow_forwardThe diagram below gives part of the graph of function f.. For a<x<b, all of the following are true: f(x)<0 , f′(x)>0 and |x|<12 Find a and b. Write your answer in the form a, b without spaces, e.g. for a=−4 and b=3 write −4,3.arrow_forwardPls help ASAParrow_forward
- Consider the following model to grow simple networks. At time t = 1 we start with a complete network with no = 6 nodes. At each time step t > 1 a new node is added to the network. The node arrives together with m = 2 new links, which are connected to m = 2 different nodes already present in the network. The probability II, that a new link is connected to node i is: N(t-1) II¿ = ki - 1 Ꮓ with Z=(k-1) j=1 where ki is the degree of node i, and N(t - 1) is the number of nodes in the network at timet - 1.arrow_forward12. Consider the function f(x) = = -3 x 2x a) Construct a table of values for the function. Use an image or transformation table. b) Graph the function on the grid provided. Use at least four points. 10 8 6 4 2 -10 -8 -6 -4 -2 4 6 8 10 -2 -4 -6 -8 -10 to 2arrow_forwardDraw the function of y = x 2 / 3 + x2arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
Algebra and Trigonometry (6th Edition)
Algebra
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:PEARSON
Contemporary Abstract Algebra
Algebra
ISBN:9781305657960
Author:Joseph Gallian
Publisher:Cengage Learning
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Algebra And Trigonometry (11th Edition)
Algebra
ISBN:9780135163078
Author:Michael Sullivan
Publisher:PEARSON
Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:9780980232776
Author:Gilbert Strang
Publisher:Wellesley-Cambridge Press
College Algebra (Collegiate Math)
Algebra
ISBN:9780077836344
Author:Julie Miller, Donna Gerken
Publisher:McGraw-Hill Education
Sine, Cosine and Tangent graphs explained + how to sketch | Math Hacks; Author: Math Hacks;https://www.youtube.com/watch?v=z9mqGopdUQk;License: Standard YouTube License, CC-BY