
Concept explainers
A large, flat sheet carries a uniformly distributed
the sheet radiates an
(a) Find the wave function for the electric field of the wave to the right of the sheet. (b) Find the Poynting vector as a function of x and t. (c) Find the intensity of the wave. (d) What If? If the sheet is to emit
Figure P33.28
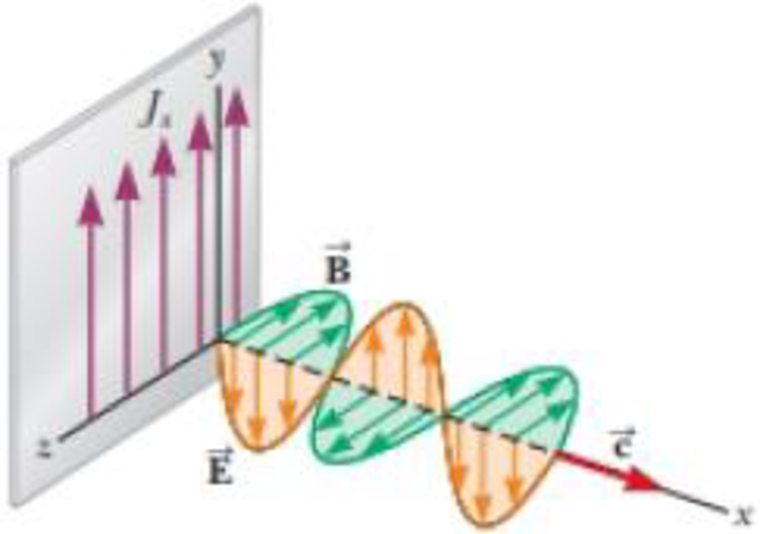
(a)
The wave function for the electric field of the wave to the right of the sheet.
Answer to Problem 46P
The wave function for the electric field of the wave to the right of the sheet is
Explanation of Solution
Given info: The wave function for the magnetic field of the wave to the right of the sheet is
Write the Maxwell’s third equation,
Here,
Substitute
Integrating the above equation with respect to
Substitute
The direction of electric field must be perpendicular to the direction of propagation
Conclusion:
Therefore, the wave function for the electric field of the wave to the right of the sheet is
(b)
The Poynting vector as a function of
Answer to Problem 46P
The Poynting vector as a function of
Explanation of Solution
Given info: The wave function for the magnetic field of the wave to the right of the sheet is
Write the formula to calculate the Poynting vector.
Here,
Substitute
Conclusion:
Therefore, the Poynting vector as a function of
(c)
The intensity of the wave.
Answer to Problem 46P
The intensity of the wave is
Explanation of Solution
Given info: The wave function for the magnetic field of the wave to the right of the sheet is
The wave function for the magnetic field of the wave is.
The maximum value of
The wave function for the electric field of the wave is.
The maximum value of
Write the formula to calculate the intensity of the wave is,
Here,
Substitute
Conclusion:
Therefore, the intensity of the wave is
(d)
The maximum value of sinusoidal current density.
Answer to Problem 46P
The maximum value of sinusoidal current density is
Explanation of Solution
Given info: The intensity of the wave is
The intensity of the wave from part (c) is,
Here,
Rearrange the above expression for
Substitute
Conclusion:
Therefore, the maximum value of sinusoidal current density is
Want to see more full solutions like this?
Chapter 34 Solutions
Physics for Scientists and Engineers with Modern Physics, Technology Update
- How can i solve this if n1 (refractive index of gas) and n2 (refractive index of plastic) is not known. And the brewsters angle isn't knownarrow_forward2. Consider the situation described in problem 1 where light emerges horizontally from ground level. Take k = 0.0020 m' and no = 1.0001 and find at which horizontal distance, x, the ray reaches a height of y = 1.5 m.arrow_forward2-3. Consider the situation of the reflection of a pulse at the interface of two string described in the previous problem. In addition to the net disturbances being equal at the junction, the slope of the net disturbances must also be equal at the junction at all times. Given that p1 = 4.0 g/m, H2 = 9.0 g/m and Aj = 0.50 cm find 2. A, (Answer: -0.10 cm) and 3. Ay. (Answer: 0.40 cm)please I need to show all work step by step problems 2 and 3arrow_forward
- look at answer show all work step by steparrow_forwardLook at the answer and please show all work step by steparrow_forward3. As a woman, who's eyes are h = 1.5 m above the ground, looks down the road sees a tree with height H = 9.0 m. Below the tree is what appears to be a reflection of the tree. The observation of this apparent reflection gives the illusion of water on the roadway. This effect is commonly called a mirage. Use the results of questions 1 and 2 and the principle of ray reversibility to analyze the diagram below. Assume that light leaving the top of the tree bends toward the horizontal until it just grazes ground level. After that, the ray bends upward eventually reaching the woman's eyes. The woman interprets this incoming light as if it came from an image of the tree. Determine the size, H', of the image. (Answer 8.8 m) please show all work step by steparrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill





