Algebra 2
Algebra 2
1st Edition
ISBN: 9780078884825
Author: McGraw-Hill/Glencoe
Publisher: Glencoe/McGraw-Hill School Pub Co
bartleby

Videos

Question
Book Icon
Chapter 3.4, Problem 3CYU
To determine

To calculate: The coordinates of the vertices of the feasible region formed by graphing the given inequalities y≥−3x+2, 9x+3y≤24 and y≥−4 . Also maximum and minimum values of the function f(x,y)=2x+14y in this region.

Expert Solution & Answer
Check Mark

Answer to Problem 3CYU

The graph of the given system of inequalities is,

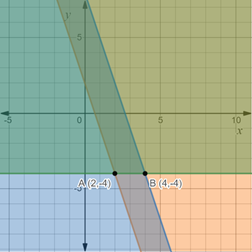
  Algebra 2, Chapter 3.4, Problem 3CYU , additional homework tip 1

The coordinates of the feasible region are A(2,−4) and B(4,−4).

The maximum value of the function is either unknown or does not exist and minimum value of the function is −52 at (2,−4).

Explanation of Solution

Given information:

The inequalities y≥−3x+2, 9x+3y≤24 and y≥−4 and the function f(x,y)=2x+14y.

Formula used:

Linear programming is a technique to find the maximum and the minimum value of a given function over a given system of some inequalities, with each inequality representing a constraint. Graph the inequalities and obtain the vertices of the feasible region (solution set). Substitute the coordinates of the feasible region in the function and determine the maximum and the minimum value.

Calculation:

Consider the provided system of inequalities y≥−3x+2, 9x+3y≤24 and y≥−4.

Recall that linear programming is a technique to find the maximum and the minimum value of a given function over a given system of some inequalities, with each inequality representing a constraint. Graph the inequalities and obtain the vertices of the feasible region (solution set).

Graph the given inequalities and locate the vertices of the feasible region.

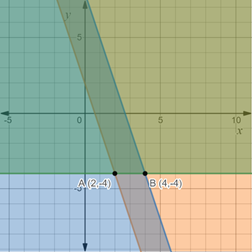
  Algebra 2, Chapter 3.4, Problem 3CYU , additional homework tip 2

Since, it is an unbounded region, the vertices of the region cannot be accurately determined. There can be infinite many points in this unbounded region, so, take the corner points where the system of inequalities cut each other, A(2,−4) and B(4,−4).

Now, to find the maximum and minimum value of the function, substitute the coordinates of the feasible region in the function and determine the maximum and the minimum value.

So, substitute A(2,−4) and B(4,−4) in the function f(x,y)=2x+14y and evaluate the maximum and minimum value as,

  (x,y)2x+14yf(x,y)(2,−4)2(2)+14(−4)−52(4,−4)2(4)+14(−4)−48

From the above table, it is observed that the minimum value of the function is −52 at (2,−4) because there are no more points below which can give minimum value of the function.

The maximum value of function is unknown or does not exist because there are infinite many points in the unbounded region which can give different maximum values at different points. So, the maximum value of function is either unknown or does not exist.

Thus, graph of the given system of inequalities is,

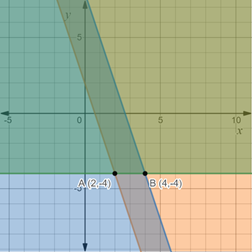
  Algebra 2, Chapter 3.4, Problem 3CYU , additional homework tip 3

The coordinates of the feasible region are A(2,−4) and B(4,−4) and the maximum value of the function is either unknown or does not exist and minimum value of the function is −52 at (2,−4) .

Previous
Chapter 3.4, Problem 2CYU
Next
Chapter 3.4, Problem 4CYU

Chapter 3 Solutions

Algebra 2

Ch. 3.1 - Prob. 1ACYPCh. 3.1 - Prob. 1BCYPCh. 3.1 - Prob. 2ACYPCh. 3.1 - Prob. 2BCYPCh. 3.1 - Prob. 3CYPCh. 3.1 - Prob. 4ACYPCh. 3.1 - Prob. 4BCYPCh. 3.1 - Prob. 4CCYPCh. 3.1 - Prob. 4DCYPCh. 3.1 - Prob. 1CYU
Ch. 3.1 - Prob. 2CYUCh. 3.1 - Prob. 3CYUCh. 3.1 - Prob. 4CYUCh. 3.1 - Prob. 5CYUCh. 3.1 - Prob. 6CYUCh. 3.1 - Prob. 7CYUCh. 3.1 - Prob. 8CYUCh. 3.1 - Prob. 9CYUCh. 3.1 - Prob. 10CYUCh. 3.1 - Prob. 11CYUCh. 3.1 - Prob. 12CYUCh. 3.1 - Prob. 13PPSCh. 3.1 - Prob. 14PPSCh. 3.1 - Prob. 15PPSCh. 3.1 - Prob. 16PPSCh. 3.1 - Prob. 17PPSCh. 3.1 - Prob. 18PPSCh. 3.1 - Prob. 19PPSCh. 3.1 - Prob. 20PPSCh. 3.1 - Prob. 21PPSCh. 3.1 - Prob. 22PPSCh. 3.1 - Prob. 23PPSCh. 3.1 - Prob. 24PPSCh. 3.1 - Prob. 25PPSCh. 3.1 - Prob. 26PPSCh. 3.1 - Prob. 27PPSCh. 3.1 - Prob. 28PPSCh. 3.1 - Prob. 29PPSCh. 3.1 - Prob. 30PPSCh. 3.1 - Prob. 31PPSCh. 3.1 - Prob. 32PPSCh. 3.1 - Prob. 33PPSCh. 3.1 - Prob. 34PPSCh. 3.1 - Prob. 35PPSCh. 3.1 - Prob. 36PPSCh. 3.1 - Prob. 37PPSCh. 3.1 - Prob. 38PPSCh. 3.1 - Prob. 39PPSCh. 3.1 - Prob. 40PPSCh. 3.1 - Prob. 41PPSCh. 3.1 - Prob. 42HPCh. 3.1 - Prob. 43HPCh. 3.1 - Prob. 44HPCh. 3.1 - Prob. 45HPCh. 3.1 - Prob. 46HPCh. 3.1 - Prob. 47HPCh. 3.1 - Prob. 48HPCh. 3.1 - Prob. 49HPCh. 3.1 - Prob. 50HPCh. 3.1 - Prob. 51STPCh. 3.1 - Prob. 52STPCh. 3.1 - Prob. 53STPCh. 3.1 - Prob. 54STPCh. 3.1 - Prob. 55STPCh. 3.1 - Prob. 56STPCh. 3.1 - Prob. 57STPCh. 3.1 - Prob. 58STPCh. 3.1 - Prob. 59STPCh. 3.1 - Prob. 60STPCh. 3.1 - Prob. 61SCh. 3.1 - Prob. 62SCh. 3.1 - Prob. 63SCh. 3.1 - Prob. 64SCh. 3.1 - Prob. 65SCh. 3.1 - Prob. 66SCh. 3.1 - Prob. 1ECh. 3.1 - Prob. 2ECh. 3.1 - Prob. 3ECh. 3.1 - Prob. 4ECh. 3.1 - Prob. 5ECh. 3.1 - Prob. 6ECh. 3.1 - Prob. 7ECh. 3.1 - Prob. 8ECh. 3.1 - Prob. 9ECh. 3.1 - Prob. 10ECh. 3.2 - Prob. 1ACYPCh. 3.2 - Prob. 1BCYPCh. 3.2 - Prob. 1CCYPCh. 3.2 - Prob. 2ACYPCh. 3.2 - Prob. 2BCYPCh. 3.2 - Prob. 2CCYPCh. 3.2 - Prob. 3CYPCh. 3.2 - Prob. 4ACYPCh. 3.2 - Prob. 4BCYPCh. 3.2 - Prob. 1CYUCh. 3.2 - Prob. 2CYUCh. 3.2 - Prob. 3CYUCh. 3.2 - Prob. 4CYUCh. 3.2 - Prob. 5CYUCh. 3.2 - Prob. 6CYUCh. 3.2 - Prob. 7CYUCh. 3.2 - Prob. 8CYUCh. 3.2 - Prob. 9CYUCh. 3.2 - Prob. 10CYUCh. 3.2 - Prob. 11CYUCh. 3.2 - Prob. 12CYUCh. 3.2 - Prob. 13CYUCh. 3.2 - Prob. 14CYUCh. 3.2 - Prob. 15PPSCh. 3.2 - Prob. 16PPSCh. 3.2 - Prob. 17PPSCh. 3.2 - Prob. 18PPSCh. 3.2 - Prob. 19PPSCh. 3.2 - Prob. 20PPSCh. 3.2 - Prob. 21PPSCh. 3.2 - Prob. 22PPSCh. 3.2 - Prob. 23PPSCh. 3.2 - Prob. 24PPSCh. 3.2 - Prob. 25PPSCh. 3.2 - Prob. 26PPSCh. 3.2 - Prob. 27PPSCh. 3.2 - Prob. 28PPSCh. 3.2 - Prob. 29PPSCh. 3.2 - Prob. 30PPSCh. 3.2 - Prob. 31PPSCh. 3.2 - Prob. 32PPSCh. 3.2 - Prob. 33PPSCh. 3.2 - Prob. 34PPSCh. 3.2 - Prob. 35PPSCh. 3.2 - Prob. 36PPSCh. 3.2 - Prob. 37PPSCh. 3.2 - Prob. 38PPSCh. 3.2 - Prob. 39PPSCh. 3.2 - Prob. 40PPSCh. 3.2 - Prob. 41PPSCh. 3.2 - Prob. 42PPSCh. 3.2 - Prob. 43PPSCh. 3.2 - Prob. 44PPSCh. 3.2 - Prob. 45PPSCh. 3.2 - Prob. 46PPSCh. 3.2 - Prob. 47PPSCh. 3.2 - Prob. 48PPSCh. 3.2 - Prob. 49PPSCh. 3.2 - Prob. 50PPSCh. 3.2 - Prob. 51PPSCh. 3.2 - Prob. 52PPSCh. 3.2 - Prob. 53PPSCh. 3.2 - Prob. 54PPSCh. 3.2 - Prob. 55PPSCh. 3.2 - Prob. 56PPSCh. 3.2 - Prob. 57PPSCh. 3.2 - Prob. 58PPSCh. 3.2 - Prob. 59PPSCh. 3.2 - Prob. 60PPSCh. 3.2 - Prob. 61PPSCh. 3.2 - Prob. 62PPSCh. 3.2 - Prob. 63PPSCh. 3.2 - Prob. 64HPCh. 3.2 - Prob. 65HPCh. 3.2 - Prob. 66HPCh. 3.2 - Prob. 67HPCh. 3.2 - Prob. 68HPCh. 3.2 - Prob. 69HPCh. 3.2 - Prob. 70HPCh. 3.2 - Prob. 71HPCh. 3.2 - Prob. 72HPCh. 3.2 - Prob. 73STPCh. 3.2 - Prob. 74STPCh. 3.2 - Prob. 75STPCh. 3.2 - Prob. 76STPCh. 3.2 - Prob. 77STPCh. 3.2 - Prob. 78STPCh. 3.2 - Prob. 79STPCh. 3.2 - Prob. 80STPCh. 3.2 - Prob. 81SCh. 3.2 - Prob. 82SCh. 3.2 - Prob. 83SCh. 3.3 - Prob. 1ACYPCh. 3.3 - Prob. 1BCYPCh. 3.3 - Prob. 2ACYPCh. 3.3 - Prob. 2BCYPCh. 3.3 - Prob. 3CYPCh. 3.3 - Prob. 4ACYPCh. 3.3 - Prob. 4BCYPCh. 3.3 - Prob. 1CYUCh. 3.3 - Prob. 2CYUCh. 3.3 - Prob. 3CYUCh. 3.3 - Prob. 4CYUCh. 3.3 - Prob. 5CYUCh. 3.3 - Prob. 6CYUCh. 3.3 - Prob. 7PPSCh. 3.3 - Prob. 8PPSCh. 3.3 - Prob. 9PPSCh. 3.3 - Prob. 10PPSCh. 3.3 - Prob. 11PPSCh. 3.3 - Prob. 12PPSCh. 3.3 - Prob. 13PPSCh. 3.3 - Prob. 14PPSCh. 3.3 - Prob. 15PPSCh. 3.3 - Prob. 16PPSCh. 3.3 - Prob. 17PPSCh. 3.3 - Prob. 18PPSCh. 3.3 - Prob. 19PPSCh. 3.3 - Prob. 20PPSCh. 3.3 - Prob. 21PPSCh. 3.3 - Prob. 22PPSCh. 3.3 - Prob. 23PPSCh. 3.3 - Prob. 24PPSCh. 3.3 - Prob. 25PPSCh. 3.3 - Prob. 26PPSCh. 3.3 - Prob. 27PPSCh. 3.3 - Prob. 28PPSCh. 3.3 - Prob. 29PPSCh. 3.3 - Prob. 30PPSCh. 3.3 - Prob. 31PPSCh. 3.3 - Prob. 32PPSCh. 3.3 - Prob. 33PPSCh. 3.3 - Prob. 34PPSCh. 3.3 - Prob. 35PPSCh. 3.3 - Prob. 36PPSCh. 3.3 - Prob. 37PPSCh. 3.3 - Prob. 38PPSCh. 3.3 - Prob. 39PPSCh. 3.3 - Prob. 40PPSCh. 3.3 - Prob. 41PPSCh. 3.3 - Prob. 42PPSCh. 3.3 - Prob. 43PPSCh. 3.3 - Prob. 44PPSCh. 3.3 - Prob. 45HPCh. 3.3 - Prob. 46HPCh. 3.3 - Prob. 47HPCh. 3.3 - Prob. 48HPCh. 3.3 - Prob. 49HPCh. 3.3 - Prob. 50HPCh. 3.3 - Prob. 51HPCh. 3.3 - Prob. 52HPCh. 3.3 - Prob. 53HPCh. 3.3 - Prob. 54HPCh. 3.3 - Prob. 55STPCh. 3.3 - Prob. 56STPCh. 3.3 - Prob. 57STPCh. 3.3 - Prob. 58STPCh. 3.3 - Prob. 59STPCh. 3.3 - Prob. 60STPCh. 3.3 - Prob. 61STPCh. 3.3 - Prob. 62STPCh. 3.3 - Prob. 63SCh. 3.3 - Prob. 64SCh. 3.3 - Prob. 65SCh. 3.3 - Prob. 66SCh. 3.3 - Prob. 67SCh. 3.3 - Prob. 68SCh. 3.3 - Prob. 1ECh. 3.3 - Prob. 2ECh. 3.3 - Prob. 3ECh. 3.3 - Prob. 4ECh. 3.3 - Prob. 5ECh. 3.3 - Prob. 6ECh. 3.3 - Prob. 7ECh. 3.3 - Prob. 8ECh. 3.3 - Prob. 9ECh. 3.4 - Prob. 1ACYPCh. 3.4 - Prob. 1BCYPCh. 3.4 - Prob. 2ACYPCh. 3.4 - Prob. 2BCYPCh. 3.4 - Prob. 3CYPCh. 3.4 - Prob. 1CYUCh. 3.4 - Prob. 2CYUCh. 3.4 - Prob. 3CYUCh. 3.4 - Prob. 4CYUCh. 3.4 - Prob. 5CYUCh. 3.4 - Prob. 6CYUCh. 3.4 - Prob. 7CYUCh. 3.4 - Prob. 8PPSCh. 3.4 - Prob. 9PPSCh. 3.4 - Prob. 10PPSCh. 3.4 - Prob. 11PPSCh. 3.4 - Prob. 12PPSCh. 3.4 - Prob. 13PPSCh. 3.4 - Prob. 14PPSCh. 3.4 - Prob. 15PPSCh. 3.4 - Prob. 16PPSCh. 3.4 - Prob. 17PPSCh. 3.4 - Prob. 18PPSCh. 3.4 - Prob. 19PPSCh. 3.4 - Prob. 20PPSCh. 3.4 - Prob. 21PPSCh. 3.4 - Prob. 22PPSCh. 3.4 - Prob. 23PPSCh. 3.4 - Prob. 24PPSCh. 3.4 - Prob. 25PPSCh. 3.4 - Prob. 26PPSCh. 3.4 - Prob. 27PPSCh. 3.4 - Prob. 28PPSCh. 3.4 - Prob. 29PPSCh. 3.4 - Prob. 30HPCh. 3.4 - Prob. 31HPCh. 3.4 - Prob. 32HPCh. 3.4 - Prob. 33HPCh. 3.4 - Prob. 34HPCh. 3.4 - Prob. 35HPCh. 3.4 - Prob. 36HPCh. 3.4 - Prob. 37HPCh. 3.4 - Prob. 38STPCh. 3.4 - Prob. 39STPCh. 3.4 - Prob. 40STPCh. 3.4 - Prob. 41STPCh. 3.4 - Prob. 42STPCh. 3.4 - Prob. 43STPCh. 3.4 - Prob. 44STPCh. 3.4 - Prob. 45STPCh. 3.4 - Prob. 46STPCh. 3.4 - Prob. 47STPCh. 3.4 - Prob. 48STPCh. 3.4 - Prob. 49STPCh. 3.4 - Prob. 50SCh. 3.4 - Prob. 51SCh. 3.4 - Prob. 52SCh. 3.4 - Prob. 53SCh. 3.4 - Prob. 54SCh. 3.4 - Prob. 55SCh. 3.5 - Prob. 1ACYPCh. 3.5 - Prob. 1BCYPCh. 3.5 - Prob. 2ACYPCh. 3.5 - Prob. 2BCYPCh. 3.5 - Prob. 3CYPCh. 3.5 - Prob. 1CYUCh. 3.5 - Prob. 2CYUCh. 3.5 - Prob. 3CYUCh. 3.5 - Prob. 4CYUCh. 3.5 - Prob. 5CYUCh. 3.5 - Prob. 6CYUCh. 3.5 - Prob. 7CYUCh. 3.5 - Prob. 8PPSCh. 3.5 - Prob. 9PPSCh. 3.5 - Prob. 10PPSCh. 3.5 - Prob. 11PPSCh. 3.5 - Prob. 12PPSCh. 3.5 - Prob. 13PPSCh. 3.5 - Prob. 14PPSCh. 3.5 - Prob. 15PPSCh. 3.5 - Prob. 16PPSCh. 3.5 - Prob. 17PPSCh. 3.5 - Prob. 18PPSCh. 3.5 - Prob. 19PPSCh. 3.5 - Prob. 20PPSCh. 3.5 - Prob. 21PPSCh. 3.5 - Prob. 22PPSCh. 3.5 - Prob. 23PPSCh. 3.5 - Prob. 24HPCh. 3.5 - Prob. 25HPCh. 3.5 - Prob. 26HPCh. 3.5 - Prob. 27HPCh. 3.5 - Prob. 28HPCh. 3.5 - Prob. 29HPCh. 3.5 - Prob. 30HPCh. 3.5 - Prob. 31HPCh. 3.5 - Prob. 32HPCh. 3.5 - Prob. 33HPCh. 3.5 - Prob. 34STPCh. 3.5 - Prob. 35STPCh. 3.5 - Prob. 36STPCh. 3.5 - Prob. 37STPCh. 3.5 - Prob. 38STPCh. 3.5 - Prob. 39SCh. 3.5 - Prob. 40SCh. 3.5 - Prob. 41SCh. 3.5 - Prob. 42SCh. 3 - Prob. 1QCCh. 3 - Prob. 2QCCh. 3 - Prob. 3QCCh. 3 - Prob. 4QCCh. 3 - Prob. 5QCCh. 3 - Prob. 6QCCh. 3 - Prob. 7QCCh. 3 - Prob. 8QCCh. 3 - Prob. 9QCCh. 3 - Prob. 10QCCh. 3 - Prob. 11QCCh. 3 - Prob. 12QCCh. 3 - Prob. 13QCCh. 3 - Prob. 14QCCh. 3 - Prob. 1MCQCh. 3 - Prob. 2MCQCh. 3 - Prob. 3MCQCh. 3 - Prob. 4MCQCh. 3 - Prob. 5MCQCh. 3 - Prob. 6MCQCh. 3 - Prob. 7MCQCh. 3 - Prob. 8MCQCh. 3 - Prob. 9MCQCh. 3 - Prob. 10MCQCh. 3 - Prob. 11MCQCh. 3 - Prob. 12MCQCh. 3 - Prob. 13MCQCh. 3 - Prob. 14MCQCh. 3 - Prob. 15MCQCh. 3 - Prob. 16MCQCh. 3 - Prob. 17MCQCh. 3 - Prob. 18MCQCh. 3 - Prob. 19MCQCh. 3 - Prob. 20MCQCh. 3 - Prob. 21MCQCh. 3 - Prob. 22MCQCh. 3 - Prob. 1SGRCh. 3 - Prob. 2SGRCh. 3 - Prob. 3SGRCh. 3 - Prob. 4SGRCh. 3 - Prob. 5SGRCh. 3 - Prob. 6SGRCh. 3 - Prob. 7SGRCh. 3 - Prob. 8SGRCh. 3 - Prob. 9SGRCh. 3 - Prob. 10SGRCh. 3 - Prob. 11SGRCh. 3 - Prob. 12SGRCh. 3 - Prob. 13SGRCh. 3 - Prob. 14SGRCh. 3 - Prob. 15SGRCh. 3 - Prob. 16SGRCh. 3 - Prob. 17SGRCh. 3 - Prob. 18SGRCh. 3 - Prob. 19SGRCh. 3 - Prob. 20SGRCh. 3 - Prob. 21SGRCh. 3 - Prob. 22SGRCh. 3 - Prob. 23SGRCh. 3 - Prob. 24SGRCh. 3 - Prob. 25SGRCh. 3 - Prob. 26SGRCh. 3 - Prob. 27SGRCh. 3 - Prob. 28SGRCh. 3 - Prob. 29SGRCh. 3 - Prob. 30SGRCh. 3 - Prob. 1PTCh. 3 - Prob. 2PTCh. 3 - Prob. 3PTCh. 3 - Prob. 4PTCh. 3 - Prob. 5PTCh. 3 - Prob. 6PTCh. 3 - Prob. 7PTCh. 3 - Prob. 8PTCh. 3 - Prob. 9PTCh. 3 - Prob. 10PTCh. 3 - Prob. 11PTCh. 3 - Prob. 12PTCh. 3 - Prob. 13PTCh. 3 - Prob. 14PTCh. 3 - Prob. 15PTCh. 3 - Prob. 16PTCh. 3 - Prob. 17PTCh. 3 - Prob. 18PTCh. 3 - Prob. 19PTCh. 3 - Prob. 1ECh. 3 - Prob. 2ECh. 3 - Prob. 3ECh. 3 - Prob. 4ECh. 3 - Prob. 1STPCh. 3 - Prob. 2STPCh. 3 - Prob. 3STPCh. 3 - Prob. 4STPCh. 3 - Prob. 5STPCh. 3 - Prob. 6STPCh. 3 - Prob. 7STPCh. 3 - Prob. 8STPCh. 3 - Prob. 9STPCh. 3 - Prob. 10STPCh. 3 - Prob. 11STPCh. 3 - Prob. 12STPCh. 3 - Prob. 13STP

Additional Math Textbook Solutions

Find more solutions based on key concepts
A categorical variable has three categories, with the following frequencies of occurrence: a. Compute the perce...

Basic Business Statistics, Student Value Edition

Find how many SDs above the mean price would be predicted to cost.

Intro Stats, Books a la Carte Edition (5th Edition)

Lines in space Find an equation of the following lines or line segments. 32. The line that passes through the p...

Calculus: Early Transcendentals (2nd Edition)

The selling price of the given item.

Pre-Algebra Student Edition

CHECK POINT I Let p and q represent the following statements: p : 3 + 5 = 8 q : 2 × 7 = 20. Determine the truth...

Thinking Mathematically (6th Edition)

In Exercises 9-12, assume that 50 births are randomly selected. Use subjective judgment to describe the given n...

Elementary Statistics (13th Edition)

Knowledge Booster
Background pattern image
Algebra
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.
Recommended textbooks for you
Text book image
Algebra and Trigonometry (6th Edition)
Algebra
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:PEARSON
Text book image
Contemporary Abstract Algebra
Algebra
ISBN:9781305657960
Author:Joseph Gallian
Publisher:Cengage Learning
Text book image
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Text book image
Algebra And Trigonometry (11th Edition)
Algebra
ISBN:9780135163078
Author:Michael Sullivan
Publisher:PEARSON
Text book image
Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:9780980232776
Author:Gilbert Strang
Publisher:Wellesley-Cambridge Press
Text book image
College Algebra (Collegiate Math)
Algebra
ISBN:9780077836344
Author:Julie Miller, Donna Gerken
Publisher:McGraw-Hill Education
SEE MORE TEXTBOOKS
Matrix Factorization - Numberphile; Author: Numberphile;https://www.youtube.com/watch?v=wTUSz-HSaBg;License: Standard YouTube License, CC-BY