University Calculus
University Calculus
4th Edition
ISBN: 9780135164846
Author: Joel R. Hass, Maurice D. Weir, George B. Thomas, Jr., Przemyslaw Bogacki
Publisher: PEARSON
bartleby

Concept explainers

Equations and Inequations
Equations and inequalities describe the relationship between two mathematical expressions.
Linear Functions
A linear function can just be a constant, or it can be the constant multiplied with the variable like x or y. If the variables are of the form, x2, x1/2 or y2 it is not linear. The exponent over the variables should always be 1.
bartleby

Videos

Textbook Question
Book Icon
Chapter 3.4, Problem 17E

Launching a rocket

When a model rocket is launched, the propellant burns for a few seconds, accelerating the rocket upward. After burnout, the rocket coasts upward for a while and then begins to fall. A small explosive charge pops out a parachute shortly after the rocket starts down. The parachute slows the rocket to keep it from breaking when it lands.

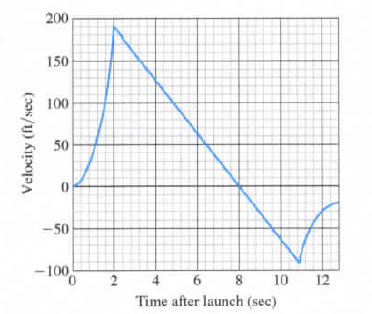
The figure here shows velocity data from the flight of the model rocket. Use the data to answer the following.

  1. How fast was the rocket climbing when the engine stopped?

  2. For how many seconds did the engine burn?

  3. When did the rocket reach its highest point? What was its velocity then?

  4. When did the parachute pop out? How fast was the rocket falling then?

  5. How long did the rocket fall before the parachute opened?

  6. When was the rocket’s acceleration greatest?

  7. When was the acceleration constant? What was its value then(to the nearest integer)?

Chapter 3.4, Problem 17E, 17. Launching a rocket When a model rocket is launched , the propellant burns for a few seconds,

Expert Solution & Answer
Check Mark

Want to see the full answer?

Check out a sample textbook solution
Blurred answer
Previous
Chapter 3.4, Problem 16E
Next
Chapter 3.4, Problem 18E
Students have asked these similar questions
1/ Solve the following: 1 x + X + cos(3X) -75 -1 2 2 (5+1) e 5² + 5 + 1 3 L -1 1 5² (5²+1) 1 5(5-5)
I need expert handwritten solution.to this integral
How to understand and learn Laurent's serial and what's the point of Laurent's serial And what are the steps of a smooth solution for Laurent

Chapter 3 Solutions

University Calculus

Ch. 3.1 - Slopes and Tangent Lines In exercises 1-4, use the...Ch. 3.1 - Prob. 2ECh. 3.1 - Prob. 3ECh. 3.1 - Prob. 4ECh. 3.1 - Prob. 5ECh. 3.1 - Prob. 6ECh. 3.1 - Prob. 7ECh. 3.1 - Prob. 8ECh. 3.1 - Prob. 9ECh. 3.1 - Prob. 10E
Ch. 3.1 - Prob. 11ECh. 3.1 - Prob. 12ECh. 3.1 - Prob. 13ECh. 3.1 - Prob. 14ECh. 3.1 - Prob. 15ECh. 3.1 - Prob. 16ECh. 3.1 - Prob. 17ECh. 3.1 - Prob. 18ECh. 3.1 - Prob. 19ECh. 3.1 - Prob. 20ECh. 3.1 - Prob. 21ECh. 3.1 - Prob. 22ECh. 3.1 - Interpreting Derivative Values 23. Growth Of The...Ch. 3.1 - Effectiveness of a drug On a scale 0 to 1, the...Ch. 3.1 - Prob. 25ECh. 3.1 - Prob. 26ECh. 3.1 - Find equations of all lines having slope -1 that...Ch. 3.1 - Find an equation of the straight line having slope...Ch. 3.1 - Rates of change Object dropped from the tower An...Ch. 3.1 - Speed of a rocket At t sec after liftoff, the...Ch. 3.1 - 31. Circle’s changing area What is the rate of...Ch. 3.1 - Rates of changes Balls changing volume What is the...Ch. 3.1 - Rates of changes Show that the line y=mx+b Is its...Ch. 3.1 - Rates of change 34. Find the slope of the tangent...Ch. 3.1 - Testing for tangent lines 35. Does the graph of...Ch. 3.1 - Testing for Tangent Lines 36. Does the graph...Ch. 3.1 - Does the graph of f(x)={1,x00,x=01,x0 Have a...Ch. 3.1 - Does the graph of U(x)={0,x01,x0 Have a vertical...Ch. 3.1 - T Graph the curve in Exercises 39-48. Where do...Ch. 3.1 - T Graph the curve in Exercises 39-48. Where do the...Ch. 3.1 - T Graph the curve in Exercises 39-48. Where do the...Ch. 3.1 - T Graph the curve in Exercises 39-48. Where do...Ch. 3.1 - T Graph the curve in Exercises 39-48. Where do the...Ch. 3.1 - T Graph the curve in Exercises 39-48. Where do...Ch. 3.1 - T Graph the curve in Exercises 39-48. Where do...Ch. 3.1 - T Graph the curve in Exercises 39-48. Where do the...Ch. 3.1 - T Graph the curve in Exercises 39-48. Where do...Ch. 3.1 - T Graph the curve in Exercises 39-48. Where do...Ch. 3.1 - COMPUTER EXPLORATIONS Use a CAS to perform the...Ch. 3.1 - COMPUTER EXPLORATIONS Use a CAS to perform the...Ch. 3.1 - COMPUTER EXPLORATIONS Use a CAS to perform the...Ch. 3.1 - COMPUTER EXPLORATIONS Use a CAS to perform the...Ch. 3.2 - Using the definition, calculate the derivatives of...Ch. 3.2 - Using the definition, calculate the derivatives of...Ch. 3.2 - Using the definition, calculate the derivatives of...Ch. 3.2 - Using the definition, calculate the derivatives of...Ch. 3.2 - Using the definition, calculate the derivatives of...Ch. 3.2 - Using the definition, calculate the derivatives of...Ch. 3.2 - In Exercises 7-12, find the indicated derivatives....Ch. 3.2 - In Exercises 7-12, find the indicated...Ch. 3.2 - In Exercises 7-12, find the indicated derivatives....Ch. 3.2 - In Exercises 7-12, find the indicated...Ch. 3.2 - In Exercises 7-12, find the indicated...Ch. 3.2 - In Exercises 7-12, find the indicated...Ch. 3.2 - In Exercises 13-16, differentiate the functions...Ch. 3.2 - In Exercises 13-16, differentiate the functions...Ch. 3.2 - In Exercises 13-16, differentiate the functions...Ch. 3.2 - In Exercises 13-16, differentiate the functions...Ch. 3.2 - In Exercises 17-18, differentiate the functions....Ch. 3.2 - In Exercises 17-18, differentiate the functions....Ch. 3.2 - In Exercises 19-22, find the values of the...Ch. 3.2 - In Exercises 19-22, find the values of the...Ch. 3.2 - In Exercises 19-22, find the values of the...Ch. 3.2 - In Exercises 19-22, find the values of the...Ch. 3.2 - Prob. 23ECh. 3.2 - Prob. 24ECh. 3.2 - Prob. 25ECh. 3.2 - Prob. 26ECh. 3.2 - Prob. 27ECh. 3.2 - Prob. 28ECh. 3.2 - Prob. 29ECh. 3.2 - Prob. 30ECh. 3.2 - Prob. 31ECh. 3.2 - Prob. 32ECh. 3.2 - 33. Growth in the economy The graph in the...Ch. 3.2 - Fruit flies (Continuation of Example 4, Section...Ch. 3.2 - Prob. 35ECh. 3.2 - Prob. 36ECh. 3.2 - Prob. 37ECh. 3.2 - Prob. 38ECh. 3.2 - Prob. 39ECh. 3.2 - Prob. 40ECh. 3.2 - Prob. 41ECh. 3.2 - Prob. 42ECh. 3.2 - Prob. 43ECh. 3.2 - Prob. 44ECh. 3.2 - Prob. 45ECh. 3.2 - Prob. 46ECh. 3.2 - Prob. 47ECh. 3.2 - Prob. 48ECh. 3.2 - Prob. 49ECh. 3.2 - Prob. 50ECh. 3.2 - Prob. 51ECh. 3.2 - Prob. 52ECh. 3.2 - Prob. 53ECh. 3.2 - Prob. 54ECh. 3.2 - Prob. 55ECh. 3.2 - Prob. 56ECh. 3.2 - 57. Derivative of Does knowing that function is...Ch. 3.2 - Prob. 58ECh. 3.2 - Prob. 59ECh. 3.2 - Prob. 60ECh. 3.2 - Prob. 61ECh. 3.2 - Prob. 62ECh. 3.2 - Prob. 63ECh. 3.2 - 64. Weierstrass’s nowhere differentiable...Ch. 3.2 - Prob. 65ECh. 3.2 - Prob. 66ECh. 3.2 - Prob. 69ECh. 3.2 - COMPUTER EXPLORATIONS Use a CAS to perform the...Ch. 3.3 - Prob. 1ECh. 3.3 - Prob. 2ECh. 3.3 - Prob. 3ECh. 3.3 - Prob. 4ECh. 3.3 - Prob. 5ECh. 3.3 - Prob. 6ECh. 3.3 - Prob. 7ECh. 3.3 - Prob. 8ECh. 3.3 - Prob. 9ECh. 3.3 - Prob. 10ECh. 3.3 - Prob. 11ECh. 3.3 - Prob. 12ECh. 3.3 - Prob. 13ECh. 3.3 - Prob. 14ECh. 3.3 - Prob. 15ECh. 3.3 - Prob. 16ECh. 3.3 - Prob. 17ECh. 3.3 - Prob. 18ECh. 3.3 - Prob. 19ECh. 3.3 - Prob. 20ECh. 3.3 - Prob. 21ECh. 3.3 - Prob. 22ECh. 3.3 - Prob. 23ECh. 3.3 - Prob. 24ECh. 3.3 - Prob. 25ECh. 3.3 - Prob. 26ECh. 3.3 - Prob. 27ECh. 3.3 - Prob. 28ECh. 3.3 - Prob. 29ECh. 3.3 - Prob. 30ECh. 3.3 - Prob. 31ECh. 3.3 - Prob. 32ECh. 3.3 - Prob. 33ECh. 3.3 - Prob. 34ECh. 3.3 - Prob. 35ECh. 3.3 - Prob. 36ECh. 3.3 - Prob. 37ECh. 3.3 - Prob. 38ECh. 3.3 - Prob. 39ECh. 3.3 - Prob. 40ECh. 3.3 - Prob. 41ECh. 3.3 - Prob. 42ECh. 3.3 - Prob. 43ECh. 3.3 - Find the derivatives of all orders of the...Ch. 3.3 - Prob. 45ECh. 3.3 - Prob. 46ECh. 3.3 - Prob. 47ECh. 3.3 - Prob. 48ECh. 3.3 - Prob. 49ECh. 3.3 - Prob. 50ECh. 3.3 - Prob. 51ECh. 3.3 - Prob. 52ECh. 3.3 - Prob. 53ECh. 3.3 - Prob. 54ECh. 3.3 - Prob. 55ECh. 3.3 - Prob. 56ECh. 3.3 - Prob. 57ECh. 3.3 - Prob. 58ECh. 3.3 - Prob. 59ECh. 3.3 - Prob. 60ECh. 3.3 - Prob. 61ECh. 3.3 - Prob. 62ECh. 3.3 - Slopes and Tangent Lines Findall points (x, y) on...Ch. 3.3 - Prob. 64ECh. 3.3 - Prob. 65ECh. 3.3 - Prob. 66ECh. 3.3 - Prob. 67ECh. 3.3 - Prob. 68ECh. 3.3 - Prob. 69ECh. 3.3 - Prob. 70ECh. 3.3 - Prob. 71ECh. 3.3 - Prob. 72ECh. 3.3 - Prob. 73ECh. 3.3 - Prob. 74ECh. 3.3 - 75. Suppose that the function in the Derivative...Ch. 3.3 - The Reciprocal Rule The Reciprocal Rule says that...Ch. 3.3 - Generalizing the Product Rule The Derivative...Ch. 3.3 - Prob. 78ECh. 3.3 - Prob. 79ECh. 3.3 - Prob. 80ECh. 3.4 - Motion along a coordinate Line Exercises 1-6 give...Ch. 3.4 - Prob. 2ECh. 3.4 - Prob. 3ECh. 3.4 - Prob. 4ECh. 3.4 - Prob. 5ECh. 3.4 - Prob. 6ECh. 3.4 - Prob. 7ECh. 3.4 - Prob. 8ECh. 3.4 - Prob. 9ECh. 3.4 - Lunar projectile motion A rock thrown vertically...Ch. 3.4 - Finding g on a small airless planet Explorers on a...Ch. 3.4 - 12. Speeding bullet A 45- calibre bullet shot...Ch. 3.4 - Prob. 13ECh. 3.4 - Prob. 14ECh. 3.4 - Understanding Motion from Graphs 15. The...Ch. 3.4 - Prob. 16ECh. 3.4 - 17. Launching a rocket When a model rocket is...Ch. 3.4 - The accompanying figure shows the velocity v=f(t)...Ch. 3.4 - Prob. 19ECh. 3.4 - Prob. 20ECh. 3.4 - Prob. 21ECh. 3.4 - Marginal revenue Suppose that the revenue from...Ch. 3.4 - Prob. 23ECh. 3.4 - Prob. 24ECh. 3.4 - Draining a tank It takes 12 hours to drain a...Ch. 3.4 - Draining a tank The number of gallons of water in...Ch. 3.4 - Vehicular stopping distance Based on data from the...Ch. 3.4 - 28. Inflating a balloon The volume of a...Ch. 3.4 - 29. Airplane takeoff Suppose that the distance an...Ch. 3.4 - Volcanic lava fountains Although the November 1959...Ch. 3.4 - Exercise 31-34 give the position function of an...Ch. 3.4 - Exercise 31-34 give the position function of an...Ch. 3.4 - Exercise 31-34 give the position function of an...Ch. 3.4 - T Exercise 31-34 give the position function s=f(t)...Ch. 3.5 - Derivatives In Exercises 1-18, find dy/dx. 1. Ch. 3.5 - Derivatives In Exercises 1-18, find dy/dx....Ch. 3.5 - Derivatives In Exercises 1-18, find dy/dx. 3. Ch. 3.5 - Derivatives In Exercises 1-18, find dy/dx....Ch. 3.5 - Derivatives In Exercises 1-18, find dy/dx. 5. Ch. 3.5 - Derivatives In Exercises 1-18, find dy/dx....Ch. 3.5 - Derivatives In Exercises 1-18, find dy/dx....Ch. 3.5 - Derivatives In Exercises 1-18, find dy/dx. 8. Ch. 3.5 - Derivatives In Exercises 1-18, find dy/dx....Ch. 3.5 - Derivatives In Exercises 1-18, find dy/dx. 10. Ch. 3.5 - Derivatives In Exercises 1-18, find dy/dx. 11. Ch. 3.5 - Derivatives In Exercises 1-18, find dy/dx. 12. Ch. 3.5 - Derivatives In Exercises 1-18, find dy/dx. 13. Ch. 3.5 - Derivatives In Exercises 1-18, find dy/dx. 14. Ch. 3.5 - Derivatives In Exercises 1-18, find dy/dx. 15. Ch. 3.5 - Derivatives In Exercises 1-18, find dy/dx....Ch. 3.5 - Derivatives In Exercises 1-18, find dy/dx....Ch. 3.5 - Derivatives In Exercises 1-18, find dy/dx....Ch. 3.5 - Derivatives In Exercises 19-22, find ds/dt....Ch. 3.5 - Derivatives In Exercises 19-22, find ds/dt. 20. Ch. 3.5 - Derivatives In Exercises 19-22, find ds/dt....Ch. 3.5 - Derivatives In Exercises 19-22, find ds/dt. 22. Ch. 3.5 - Derivatives In Exercises 23-26, find dr/dθ. 23. Ch. 3.5 - Derivatives In Exercises 23-26, find dr/d....Ch. 3.5 - Derivatives In Exercises 23-26, find dr/dθ. 25. Ch. 3.5 - Derivatives In Exercises 23-26, find dr/dθ. 26. Ch. 3.5 - Derivatives In Exercises 27-32, find dp/dq. 27. Ch. 3.5 - Derivatives In Exercises 27-32, find dp/dq. 28. Ch. 3.5 - Derivatives In Exercises 27-32, find dp/dq....Ch. 3.5 - Derivatives In Exercises 27-32, find dp/dq. 30. Ch. 3.5 - Derivatives In Exercises 27-32, find dp/dq....Ch. 3.5 - Derivatives In Exercises 27-32, find dp/dq. 32. Ch. 3.5 - Find y if y=cscx. y=secx.Ch. 3.5 - 34. Find a. b. Ch. 3.5 - Tangent Lines In Exercises 35-38, graph the curves...Ch. 3.5 - Tangent Lines In Exercises 35-38, graph the curves...Ch. 3.5 - Tangent Lines In Exercises 35-38, graph the curves...Ch. 3.5 - Prob. 38ECh. 3.5 - Prob. 39ECh. 3.5 - Prob. 40ECh. 3.5 - Prob. 41ECh. 3.5 - Prob. 42ECh. 3.5 - Prob. 43ECh. 3.5 - Prob. 44ECh. 3.5 - Prob. 45ECh. 3.5 - Tangent Lines Find all points on the curve y=cotx,...Ch. 3.5 - Prob. 47ECh. 3.5 - Prob. 48ECh. 3.5 - Prob. 49ECh. 3.5 - Prob. 50ECh. 3.5 - Trigonometric Limits Find the limits in Exercises...Ch. 3.5 - Prob. 52ECh. 3.5 - Prob. 53ECh. 3.5 - Prob. 54ECh. 3.5 - Prob. 55ECh. 3.5 - Trigonometric Limits Find the limits in Exercises...Ch. 3.5 - Prob. 57ECh. 3.5 - Prob. 58ECh. 3.5 - Prob. 59ECh. 3.5 - Is there a value of b that will make...Ch. 3.5 - By computing the first few derivatives and looking...Ch. 3.5 - Prob. 62ECh. 3.5 - A weight is attached to a spring and reaches its...Ch. 3.5 - Prob. 64ECh. 3.5 - Prob. 65ECh. 3.5 - Prob. 66ECh. 3.5 - Prob. 67ECh. 3.5 - Prob. 68ECh. 3.5 - 69. Slopes on the graph of the tangent function...Ch. 3.5 - Exploring (sinkx)/x Graph y=(sinx)/x, y=(sin2x)/x,...Ch. 3.6 - Prob. 1ECh. 3.6 - Prob. 2ECh. 3.6 - Prob. 3ECh. 3.6 - Prob. 4ECh. 3.6 - Prob. 5ECh. 3.6 - Prob. 6ECh. 3.6 - Prob. 7ECh. 3.6 - Prob. 8ECh. 3.6 - Prob. 9ECh. 3.6 - Prob. 10ECh. 3.6 - Prob. 11ECh. 3.6 - Prob. 12ECh. 3.6 - Prob. 13ECh. 3.6 - Prob. 14ECh. 3.6 - Prob. 15ECh. 3.6 - Prob. 16ECh. 3.6 - Prob. 17ECh. 3.6 - Prob. 18ECh. 3.6 - Prob. 19ECh. 3.6 - Prob. 20ECh. 3.6 - Prob. 21ECh. 3.6 - Prob. 22ECh. 3.6 - Prob. 23ECh. 3.6 - Prob. 24ECh. 3.6 - Prob. 25ECh. 3.6 - Prob. 26ECh. 3.6 - Prob. 27ECh. 3.6 - Prob. 28ECh. 3.6 - Prob. 29ECh. 3.6 - Prob. 30ECh. 3.6 - Prob. 31ECh. 3.6 - Prob. 32ECh. 3.6 - Prob. 33ECh. 3.6 - Prob. 34ECh. 3.6 - Prob. 35ECh. 3.6 - Prob. 36ECh. 3.6 - Prob. 37ECh. 3.6 - Prob. 38ECh. 3.6 - Prob. 39ECh. 3.6 - Prob. 40ECh. 3.6 - Prob. 41ECh. 3.6 - Prob. 42ECh. 3.6 - Prob. 43ECh. 3.6 - Prob. 44ECh. 3.6 - Prob. 45ECh. 3.6 - Prob. 46ECh. 3.6 - Prob. 47ECh. 3.6 - Prob. 48ECh. 3.6 - Prob. 49ECh. 3.6 - Prob. 50ECh. 3.6 - Prob. 51ECh. 3.6 - Prob. 52ECh. 3.6 - Prob. 53ECh. 3.6 - Prob. 54ECh. 3.6 - Prob. 55ECh. 3.6 - Prob. 56ECh. 3.6 - Prob. 57ECh. 3.6 - Prob. 58ECh. 3.6 - Prob. 59ECh. 3.6 - Prob. 60ECh. 3.6 - Prob. 61ECh. 3.6 - Prob. 62ECh. 3.6 - Prob. 63ECh. 3.6 - Prob. 64ECh. 3.6 - Prob. 65ECh. 3.6 - Prob. 66ECh. 3.6 - Prob. 67ECh. 3.6 - Prob. 68ECh. 3.6 - Prob. 69ECh. 3.6 - Prob. 70ECh. 3.6 - Prob. 71ECh. 3.6 - Prob. 72ECh. 3.6 - Prob. 73ECh. 3.6 - Prob. 74ECh. 3.6 - Prob. 75ECh. 3.6 - Prob. 76ECh. 3.6 - Prob. 77ECh. 3.6 - Prob. 78ECh. 3.6 - Prob. 79ECh. 3.6 - Prob. 80ECh. 3.6 - Prob. 81ECh. 3.6 - Prob. 82ECh. 3.6 - Prob. 83ECh. 3.6 - Prob. 84ECh. 3.6 - Prob. 85ECh. 3.6 - Prob. 86ECh. 3.6 - Prob. 87ECh. 3.6 - Prob. 88ECh. 3.6 - Prob. 89ECh. 3.6 - Prob. 90ECh. 3.6 - Prob. 91ECh. 3.6 - Prob. 92ECh. 3.6 - Find dy/dx if y=x by using the Chain Rule with y...Ch. 3.6 - Prob. 94ECh. 3.6 - Prob. 95ECh. 3.6 - Prob. 96ECh. 3.6 - 97. a. Find the tangent line to the curve at ....Ch. 3.6 - Slopes on sine curves Find equations for the...Ch. 3.6 - Running machinery too fast Suppose that a piston...Ch. 3.6 - Prob. 100ECh. 3.6 - Prob. 101ECh. 3.6 - Constant acceleration Suppose that the velocity of...Ch. 3.6 - Prob. 103ECh. 3.6 - Prob. 104ECh. 3.6 - Prob. 105ECh. 3.6 - Prob. 106ECh. 3.6 - 107. The derivative of Graph the function for ....Ch. 3.6 - Prob. 108ECh. 3.6 - Prob. 109ECh. 3.6 - Prob. 110ECh. 3.6 - Prob. 111ECh. 3.6 - Prob. 112ECh. 3.6 - Prob. 113ECh. 3.7 - Prob. 1ECh. 3.7 - Use implicit differentiation to find dy/dx in...Ch. 3.7 - Prob. 3ECh. 3.7 - Use implicit differentiation to find dy/dx in...Ch. 3.7 - Use implicit differentiation to find dy/dx in...Ch. 3.7 - Use implicit differentiation to find dy/dx in...Ch. 3.7 - Use implicit differentiation to find dy/dx in...Ch. 3.7 - Use implicit differentiation to find dy/dx in...Ch. 3.7 - Use implicit differentiation to find dy/dx in...Ch. 3.7 - Use implicit differentiation to find dy/dx in...Ch. 3.7 - Use implicit differentiation to find dy/dx in...Ch. 3.7 - Use implicit differentiation to find dy/dx in...Ch. 3.7 - Use implicit differentiation to find dy/dx in...Ch. 3.7 - Use implicit differentiation to find dy/dx in...Ch. 3.7 - Use implicit differentiation to find dy/dx in...Ch. 3.7 - Use implicit differentiation to find dy/dx in...Ch. 3.7 - Find in Exercises 17-20. 17. Ch. 3.7 - Find in Exercises 17-20. 18. Ch. 3.7 - Find dr/d in Exercises 17-20. sin(r)=12Ch. 3.7 - Prob. 20ECh. 3.7 - Second Derivatives In Exercises 21-28, use...Ch. 3.7 - Second Derivatives In Exercises 21-28, use...Ch. 3.7 - Second Derivatives In Exercises 21-28, use...Ch. 3.7 - Second Derivatives In Exercises 21-28, use...Ch. 3.7 - Second Derivatives In Exercises 21-28, use...Ch. 3.7 - Second Derivatives In Exercises 21-28, use...Ch. 3.7 - Second Derivatives In Exercises 21-28, use...Ch. 3.7 - Second Derivatives In Exercises 21-28, use...Ch. 3.7 - 29. If find the value of at the point (2, 2). Ch. 3.7 - 30. If find the value of at the point (0, -1). Ch. 3.7 - In Exercises 31 and 32, find the slope of the...Ch. 3.7 - In Exercises 31 and 32, find the slope of the...Ch. 3.7 - Prob. 33ECh. 3.7 - Slopes, Tangent Lines, and Normal Lines In...Ch. 3.7 - Slopes, Tangent Lines, and Normal Lines In...Ch. 3.7 - Slopes, Tangent Lines, and Normal Lines In...Ch. 3.7 - Slopes, Tangent Lines, and Normal Lines In...Ch. 3.7 - Slopes, Tangent Lines, and Normal Lines In...Ch. 3.7 - Slopes, Tangent Lines, and Normal Lines In...Ch. 3.7 - Slopes, Tangent Lines, and Normal Lines In...Ch. 3.7 - Slopes, Tangent Lines, and Normal Lines In...Ch. 3.7 - Slopes, Tangent Lines, and Normal Lines In...Ch. 3.7 - 43. Parallel tangent lines Find the two points...Ch. 3.7 - 44. Normal lines parallel to a line Find the...Ch. 3.7 - 45. The eight curve Find the slopes of the curve...Ch. 3.7 - The cissoids of Diocles (from about 200 B.C.) Find...Ch. 3.7 - The devils curve (Gabriel Cramer, 1750) Find the...Ch. 3.7 - 48. The folium of Descartes (See Figure 3.29) a....Ch. 3.7 - 49. Intersecting normal line The line that is...Ch. 3.7 - Power rule for rational exponents Let p and q be...Ch. 3.7 - 51. Normal lines to a parabola Show that if it is...Ch. 3.7 - Is there anything special about the tangent lines...Ch. 3.7 - 53. Verify that the following pairs of curves meet...Ch. 3.7 - Prob. 54ECh. 3.7 - Prob. 55ECh. 3.7 - Prob. 56ECh. 3.7 - Prob. 57ECh. 3.7 - Prob. 58ECh. 3.8 - Prob. 1ECh. 3.8 - Prob. 2ECh. 3.8 - Prob. 3ECh. 3.8 - Prob. 4ECh. 3.8 - Prob. 5ECh. 3.8 - Prob. 6ECh. 3.8 - Prob. 7ECh. 3.8 - Prob. 8ECh. 3.8 - Prob. 9ECh. 3.8 - Prob. 10ECh. 3.8 - Prob. 11ECh. 3.8 - Prob. 12ECh. 3.8 - Prob. 13ECh. 3.8 - Prob. 14ECh. 3.8 - Prob. 15ECh. 3.8 - Prob. 16ECh. 3.8 - Prob. 17ECh. 3.8 - Prob. 18ECh. 3.8 - Prob. 19ECh. 3.8 - Prob. 20ECh. 3.8 - Prob. 21ECh. 3.8 - Prob. 22ECh. 3.8 - Prob. 23ECh. 3.8 - Derivatives of Logarithms In Exercises 11-40, find...Ch. 3.8 - Prob. 25ECh. 3.8 - Prob. 26ECh. 3.8 - Prob. 27ECh. 3.8 - Prob. 28ECh. 3.8 - Prob. 29ECh. 3.8 - Prob. 30ECh. 3.8 - Prob. 31ECh. 3.8 - Prob. 32ECh. 3.8 - Prob. 33ECh. 3.8 - Prob. 34ECh. 3.8 - Prob. 35ECh. 3.8 - Prob. 36ECh. 3.8 - Prob. 37ECh. 3.8 - Prob. 38ECh. 3.8 - Prob. 39ECh. 3.8 - Prob. 40ECh. 3.8 - Prob. 41ECh. 3.8 - Prob. 42ECh. 3.8 - Prob. 43ECh. 3.8 - Prob. 44ECh. 3.8 - Prob. 45ECh. 3.8 - Prob. 46ECh. 3.8 - Prob. 47ECh. 3.8 - Prob. 48ECh. 3.8 - Prob. 49ECh. 3.8 - Prob. 50ECh. 3.8 - Prob. 51ECh. 3.8 - Prob. 52ECh. 3.8 - Prob. 53ECh. 3.8 - Prob. 54ECh. 3.8 - Prob. 55ECh. 3.8 - Prob. 56ECh. 3.8 - Prob. 57ECh. 3.8 - Prob. 58ECh. 3.8 - Prob. 59ECh. 3.8 - Prob. 60ECh. 3.8 - Prob. 61ECh. 3.8 - Prob. 62ECh. 3.8 - Prob. 63ECh. 3.8 - Prob. 64ECh. 3.8 - Prob. 65ECh. 3.8 - Prob. 66ECh. 3.8 - Prob. 67ECh. 3.8 - Prob. 68ECh. 3.8 - Prob. 69ECh. 3.8 - Prob. 70ECh. 3.8 - Prob. 71ECh. 3.8 - Prob. 72ECh. 3.8 - Prob. 73ECh. 3.8 - Prob. 74ECh. 3.8 - Prob. 75ECh. 3.8 - Prob. 76ECh. 3.8 - Prob. 77ECh. 3.8 - Prob. 78ECh. 3.8 - Prob. 79ECh. 3.8 - Prob. 80ECh. 3.8 - Prob. 81ECh. 3.8 - Prob. 82ECh. 3.8 - Prob. 83ECh. 3.8 - Prob. 84ECh. 3.8 - Prob. 85ECh. 3.8 - Prob. 86ECh. 3.8 - Prob. 87ECh. 3.8 - Prob. 88ECh. 3.8 - Prob. 89ECh. 3.8 - Prob. 90ECh. 3.8 - Prob. 91ECh. 3.8 - Prob. 92ECh. 3.8 - Prob. 93ECh. 3.8 - Prob. 94ECh. 3.8 - Prob. 95ECh. 3.8 - Prob. 96ECh. 3.8 - Prob. 97ECh. 3.8 - Prob. 98ECh. 3.8 - Prob. 99ECh. 3.8 - Prob. 100ECh. 3.8 - Prob. 101ECh. 3.8 - Prob. 102ECh. 3.8 - Prob. 103ECh. 3.8 - Prob. 104ECh. 3.9 - Prob. 1ECh. 3.9 - Prob. 2ECh. 3.9 - Prob. 3ECh. 3.9 - Prob. 4ECh. 3.9 - Prob. 5ECh. 3.9 - Prob. 6ECh. 3.9 - Prob. 7ECh. 3.9 - Prob. 8ECh. 3.9 - Prob. 9ECh. 3.9 - Prob. 10ECh. 3.9 - Prob. 11ECh. 3.9 - Prob. 12ECh. 3.9 - Prob. 13ECh. 3.9 - Prob. 14ECh. 3.9 - Prob. 15ECh. 3.9 - Prob. 16ECh. 3.9 - Prob. 17ECh. 3.9 - Prob. 18ECh. 3.9 - Prob. 19ECh. 3.9 - Prob. 20ECh. 3.9 - Prob. 21ECh. 3.9 - Prob. 22ECh. 3.9 - Prob. 23ECh. 3.9 - Finding Derivatives In Exercises 21-42, find the...Ch. 3.9 - Finding Derivatives In Exercises 21-42, find the...Ch. 3.9 - Finding Derivatives In Exercises 21-42, find the...Ch. 3.9 - Prob. 27ECh. 3.9 - Finding Derivatives In Exercises 21-42, find the...Ch. 3.9 - Finding Derivatives In Exercises 21-42, find the...Ch. 3.9 - Finding Derivatives In Exercises 21-42, find the...Ch. 3.9 - Finding Derivatives In Exercises 21-42, find the...Ch. 3.9 - Prob. 32ECh. 3.9 - Finding Derivatives In Exercises 21-42, find the...Ch. 3.9 - Finding Derivatives In Exercises 21-42, find the...Ch. 3.9 - Finding Derivatives In Exercises 21-42, find the...Ch. 3.9 - Finding Derivatives In Exercises 21-42, find the...Ch. 3.9 - Finding Derivatives In Exercises 21-42, find the...Ch. 3.9 - Finding Derivatives In Exercises 21-42, find the...Ch. 3.9 - Finding Derivatives In Exercises 21-42, find the...Ch. 3.9 - Finding Derivatives In Exercises 21-42, find the...Ch. 3.9 - Finding Derivatives In Exercises 21-42, find the...Ch. 3.9 - Finding Derivatives In Exercises 21-42, find the...Ch. 3.9 - For problems 43-46 use implicit differentiation to...Ch. 3.9 - For problems 43-46 use implicit differentiation to...Ch. 3.9 - For problems 43-46 use implicit differentiation to...Ch. 3.9 - For problems 43-46 use implicit differentiation to...Ch. 3.9 - You are sitting in a classroom next to the wall...Ch. 3.9 - Prob. 48ECh. 3.9 - Here is an informal proof that tan11+tan12+tan13=....Ch. 3.9 - 50. Two derivations of the identity a....Ch. 3.9 - Which of the expressions in Exercises 51-54 are...Ch. 3.9 - Which of the expressions in Exercises 51-54 are...Ch. 3.9 - Prob. 53ECh. 3.9 - Which of the expressions in Exercises 51-54 are...Ch. 3.9 - 55. Use the identity to derive the formula for the...Ch. 3.9 - Derive the formula dydx=11+x2 for the derivative...Ch. 3.9 - 57. Use the Derivative Rule in Section 3.8,...Ch. 3.9 - 58. Use the identity to derive the formula for the...Ch. 3.9 - What is special about the functions...Ch. 3.9 - What is special about the functions f(x)=sin11x2+1...Ch. 3.9 - T Find the values of sec11.5 csc1(1.5) cot12Ch. 3.9 - 62. Find the values of b. ...Ch. 3.9 - Prob. 63ECh. 3.9 - Prob. 64ECh. 3.9 - Prob. 65ECh. 3.9 - Prob. 66ECh. 3.9 - Newtons serpentine Graph Newtons serpentine,...Ch. 3.9 - Graph the rational function y=(2x2)/x2. Then graph...Ch. 3.9 - 69. Graph together with its first two...Ch. 3.9 - Graph f(x)=tan1x together with its first two...Ch. 3.10 - 1. Area Suppose that the radius r and area of a...Ch. 3.10 - 2. Surface area Suppose that the radius r and...Ch. 3.10 - Assume that y=5x and dx/dt=2. Find dy/dt.Ch. 3.10 - Assume that 2x+3y=12 and dy/dt=2. Find dx/dt.Ch. 3.10 - 5. If and then what is when ? Ch. 3.10 - If y=x3y and dy/dt=5, then what is dx/dt when y=2?Ch. 3.10 - Prob. 7ECh. 3.10 - Prob. 8ECh. 3.10 - Prob. 9ECh. 3.10 - Prob. 10ECh. 3.10 - Prob. 11ECh. 3.10 - Prob. 12ECh. 3.10 - Prob. 13ECh. 3.10 - Prob. 14ECh. 3.10 - Prob. 15ECh. 3.10 - Prob. 16ECh. 3.10 - Prob. 17ECh. 3.10 - Prob. 18ECh. 3.10 - Prob. 19ECh. 3.10 - Prob. 20ECh. 3.10 - Prob. 21ECh. 3.10 - 22. Changing dimensions in a rectangular box...Ch. 3.10 - 23. A sliding ladder A13-ft ladder is leaning...Ch. 3.10 - Prob. 24ECh. 3.10 - Flying a kite A girl flies a kite at a height of...Ch. 3.10 - Prob. 26ECh. 3.10 - 27. A growing sand pile Sand falls from a conveyor...Ch. 3.10 - Prob. 28ECh. 3.10 - Prob. 29ECh. 3.10 - A growing raindrop Suppose that a drop of mist is...Ch. 3.10 - Prob. 31ECh. 3.10 - 32. Hauling in a dinghy A dinghy is pulled toward...Ch. 3.10 - Prob. 33ECh. 3.10 - Making coffee Coffee is draining from a conical...Ch. 3.10 - Prob. 35ECh. 3.10 - 36. Moving along a parabola A particle moves along...Ch. 3.10 - 37. Motion in the plane The coordinates of a...Ch. 3.10 - Videotaping a moving car You are videotaping a...Ch. 3.10 - 39. A moving shadow A light shines from the top of...Ch. 3.10 - A buildings shadow On a morning of a day when the...Ch. 3.10 - Prob. 41ECh. 3.10 - Prob. 42ECh. 3.10 - 43. Baseball players A baseball diamond is a...Ch. 3.10 - Ships Two ships are steaming straight away from a...Ch. 3.10 - Prob. 45ECh. 3.10 - 46. Oil spill An explosion at an oil rig located...Ch. 3.10 - Prob. 47ECh. 3.11 - Prob. 1ECh. 3.11 - Prob. 2ECh. 3.11 - Prob. 3ECh. 3.11 - Prob. 4ECh. 3.11 - Prob. 5ECh. 3.11 - Common linear approximations at x=0 Find the...Ch. 3.11 - Prob. 7ECh. 3.11 - Prob. 8ECh. 3.11 - Prob. 9ECh. 3.11 - Prob. 10ECh. 3.11 - In Exercises 7-14, find a linearization at a...Ch. 3.11 - Prob. 12ECh. 3.11 - Prob. 13ECh. 3.11 - Prob. 14ECh. 3.11 - Prob. 15ECh. 3.11 - Prob. 16ECh. 3.11 - Prob. 17ECh. 3.11 - Prob. 18ECh. 3.11 - Prob. 19ECh. 3.11 - Prob. 20ECh. 3.11 - Prob. 21ECh. 3.11 - Prob. 22ECh. 3.11 - Prob. 23ECh. 3.11 - Prob. 24ECh. 3.11 - Prob. 25ECh. 3.11 - Prob. 26ECh. 3.11 - Prob. 27ECh. 3.11 - Prob. 28ECh. 3.11 - Prob. 29ECh. 3.11 - Prob. 30ECh. 3.11 - Prob. 31ECh. 3.11 - Prob. 32ECh. 3.11 - Prob. 33ECh. 3.11 - Prob. 34ECh. 3.11 - Prob. 35ECh. 3.11 - Prob. 36ECh. 3.11 - Prob. 37ECh. 3.11 - Prob. 38ECh. 3.11 - Prob. 39ECh. 3.11 - Prob. 40ECh. 3.11 - Prob. 41ECh. 3.11 - Prob. 42ECh. 3.11 - Prob. 43ECh. 3.11 - Prob. 44ECh. 3.11 - Prob. 45ECh. 3.11 - Prob. 46ECh. 3.11 - Prob. 47ECh. 3.11 - Prob. 48ECh. 3.11 - Prob. 49ECh. 3.11 - Prob. 50ECh. 3.11 - Prob. 51ECh. 3.11 - 52. The diameter of a tree was During the...Ch. 3.11 - Prob. 53ECh. 3.11 - Prob. 54ECh. 3.11 - Prob. 55ECh. 3.11 - Prob. 56ECh. 3.11 - Prob. 57ECh. 3.11 - Prob. 58ECh. 3.11 - Prob. 59ECh. 3.11 - Prob. 60ECh. 3.11 - Prob. 61ECh. 3.11 - Prob. 62ECh. 3.11 - 63. Unclogging arteries The formula , discovered...Ch. 3.11 - Prob. 64ECh. 3.11 - Prob. 65ECh. 3.11 - Prob. 66ECh. 3.11 - Prob. 67ECh. 3.11 - Prob. 68ECh. 3 - Prob. 1GYRCh. 3 - Prob. 2GYRCh. 3 - Prob. 3GYRCh. 3 - Prob. 4GYRCh. 3 - Prob. 5GYRCh. 3 - Prob. 6GYRCh. 3 - 7. How is a function’s differentiability at a...Ch. 3 - Prob. 8GYRCh. 3 - Prob. 9GYRCh. 3 - Prob. 10GYRCh. 3 - Prob. 11GYRCh. 3 - Prob. 12GYRCh. 3 - Prob. 13GYRCh. 3 - Prob. 14GYRCh. 3 - Prob. 15GYRCh. 3 - Prob. 16GYRCh. 3 - 17. What do the limits and have to do with the...Ch. 3 - Prob. 18GYRCh. 3 - Prob. 19GYRCh. 3 - 20. What is the rule for calculating the...Ch. 3 - Prob. 21GYRCh. 3 - Prob. 22GYRCh. 3 - Prob. 23GYRCh. 3 - Prob. 24GYRCh. 3 - Prob. 25GYRCh. 3 - Prob. 26GYRCh. 3 - Prob. 27GYRCh. 3 - Prob. 28GYRCh. 3 - Prob. 29GYRCh. 3 - Prob. 30GYRCh. 3 - Outline a strategy for solving related rates...Ch. 3 - Prob. 32GYRCh. 3 - If x moves from a to a nearby value a + dx, how do...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Prob. 3PECh. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Prob. 9PECh. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Prob. 17PECh. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Derivatives of Functions Find the derivatives of...Ch. 3 - Prob. 52PECh. 3 - Prob. 53PECh. 3 - Prob. 54PECh. 3 - Prob. 55PECh. 3 - Prob. 56PECh. 3 - Prob. 57PECh. 3 - Prob. 58PECh. 3 - Prob. 59PECh. 3 - Prob. 60PECh. 3 - Prob. 61PECh. 3 - Prob. 62PECh. 3 - Prob. 63PECh. 3 - Prob. 64PECh. 3 - Prob. 65PECh. 3 - Implicit Differentiation In Exercises 65-78, find...Ch. 3 - Prob. 67PECh. 3 - Prob. 68PECh. 3 - Prob. 69PECh. 3 - Prob. 70PECh. 3 - Prob. 71PECh. 3 - Prob. 72PECh. 3 - Prob. 73PECh. 3 - Prob. 74PECh. 3 - Prob. 75PECh. 3 - Prob. 76PECh. 3 - Prob. 77PECh. 3 - Prob. 78PECh. 3 - Prob. 79PECh. 3 - Prob. 80PECh. 3 - Prob. 81PECh. 3 - Prob. 82PECh. 3 - Prob. 83PECh. 3 - Prob. 84PECh. 3 - Numerical Values of Derivatives Suppose that...Ch. 3 - Numerical Values of Derivatives 86. Suppose that...Ch. 3 - Prob. 87PECh. 3 - Prob. 88PECh. 3 - Prob. 89PECh. 3 - Numerical Values of Derivatives Find the value of...Ch. 3 - Prob. 91PECh. 3 - Prob. 92PECh. 3 - Prob. 93PECh. 3 - Prob. 94PECh. 3 - Prob. 95PECh. 3 - Prob. 96PECh. 3 - Prob. 97PECh. 3 - Prob. 98PECh. 3 - Prob. 99PECh. 3 - Prob. 100PECh. 3 - Prob. 101PECh. 3 - Prob. 102PECh. 3 - Prob. 103PECh. 3 - 104. Intersecting tangent lines Show that the...Ch. 3 - Prob. 105PECh. 3 - Prob. 106PECh. 3 - Prob. 107PECh. 3 - Prob. 108PECh. 3 - Prob. 109PECh. 3 - Prob. 110PECh. 3 - Prob. 111PECh. 3 - Prob. 112PECh. 3 - Prob. 113PECh. 3 - Prob. 114PECh. 3 - Prob. 115PECh. 3 - Prob. 116PECh. 3 - Prob. 117PECh. 3 - Prob. 118PECh. 3 - Prob. 119PECh. 3 - Prob. 120PECh. 3 - Prob. 121PECh. 3 - Prob. 122PECh. 3 - Prob. 123PECh. 3 - Prob. 124PECh. 3 - Prob. 125PECh. 3 - Prob. 126PECh. 3 - Prob. 127PECh. 3 - Prob. 128PECh. 3 - Prob. 129PECh. 3 - Prob. 130PECh. 3 - Prob. 131PECh. 3 - Show how to extend the functions in Exercises 131...Ch. 3 - Prob. 133PECh. 3 - Prob. 134PECh. 3 - Prob. 135PECh. 3 - Prob. 136PECh. 3 - Prob. 137PECh. 3 - Prob. 138PECh. 3 - 139. Right circular cylinder The total surface...Ch. 3 - 140. Right circular cone The lateral surface area...Ch. 3 - Circles changing area The radius r of a circle is...Ch. 3 - Cubes changing edges The volume of a cube is...Ch. 3 - Resistors connected in parallel If two resistors...Ch. 3 - 144. Impedance in a series circuit The impedance...Ch. 3 - Speed of moving particle The coordinates of a...Ch. 3 - 146. Motion of a particle A particle moves along...Ch. 3 - 147. Draining a tank Water drains from the conical...Ch. 3 - Rotating spool Astelevision cable is pulled from a...Ch. 3 - Moving searchlight beam The figure shows a boat 1...Ch. 3 - Points moving on coordinate axes Points A and B...Ch. 3 - 151. Find the linearizations of a. at . b. at...Ch. 3 - 152. We can obtain a useful linear approximation...Ch. 3 - 153. Find the linearization of at. Ch. 3 - Find the linearization of f(x)=2/(1x)+1+x3.1 at...Ch. 3 - 155. Surface area of a cone Write a formula that...Ch. 3 - Prob. 156PECh. 3 - Compounding error The circumference of the equator...Ch. 3 - Prob. 158PECh. 3 - An equation like sin2+cos2=1 is called an identity...Ch. 3 - If the identity sin(x+a)=sinxscosa+cosxsina is...Ch. 3 - 3. a. Find values for the constants that will make...Ch. 3 - Solutions to differential equations Show that...Ch. 3 - 5. An osculating circle Find the values of and...Ch. 3 - Prob. 6AAECh. 3 - Industrial production Economists often use the...Ch. 3 - Designing a gondola The designer of a...Ch. 3 - 9. Pisa by parachute On August 5, 1988, Mike...Ch. 3 - Motion of a particle The position at time t0 of a...Ch. 3 - 11. Shooting a paper clip On Earth, you can easily...Ch. 3 - Prob. 12AAECh. 3 - Prob. 13AAECh. 3 - In Exercises 14 and 15, use implicit...Ch. 3 - Prob. 15AAECh. 3 - 16. Average and instantaneous velocity a. Show...Ch. 3 - Find all values of the constants m and b for which...Ch. 3 - Does the function f(x)={1cosxx,x00,x=0 have a...Ch. 3 - 19. a. For what values of and will be...Ch. 3 - For what values of a and b will...Ch. 3 - Odd differentiable functions Is there anything...Ch. 3 - Even differentiable functions Is there anything...Ch. 3 - Suppose that the functions f and g are defined...Ch. 3 - (Continuation of Exercise 23.) Use the result of...Ch. 3 - Is the derivative of h(x)={x2sin(1/x),x00,x=0...Ch. 3 - Prob. 29AAECh. 3 - Leibnizs rule for higher-order derivatives of...Ch. 3 - The period of a clock pendulum The period T of a...
Knowledge Booster
Background pattern image
Calculus
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Text book image
College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
Text book image
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Text book image
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Text book image
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning
Text book image
College Algebra
Algebra
ISBN:9781938168383
Author:Jay Abramson
Publisher:OpenStax
SEE MORE TEXTBOOKS
What is a Linear Equation in One Variable?; Author: Don't Memorise;https://www.youtube.com/watch?v=lDOYdBgtnjY;License: Standard YouTube License, CC-BY
Linear Equation | Solving Linear Equations | What is Linear Equation in one variable ?; Author: Najam Academy;https://www.youtube.com/watch?v=tHm3X_Ta_iE;License: Standard YouTube License, CC-BY