Elementary Geometry For College Students, 7e
Elementary Geometry For College Students, 7e
7th Edition
ISBN: 9781337614085
Author: Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher: Cengage,
bartleby

Videos

Textbook Question
Book Icon
Chapter 3.3, Problem 41E

In Exercises 39 to 41 , complete each proof.

Given: Isosceles Δ M N P

with vertex P

Isosceles Δ M N Q

with vertex Q

Prove: Δ M Q P ≅ Δ N Q P

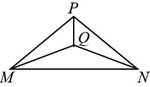
Chapter 3.3, Problem 41E, In Exercises 39 to 41, complete each proof. Given: Isosceles MNP with vertex P Isosceles MNQ with

Expert Solution & Answer
Check Mark

Want to see the full answer?

Check out a sample textbook solution
Blurred answer
Previous
Chapter 3.3, Problem 40E
Next
Chapter 3.3, Problem 42E
Students have asked these similar questions
Qll consider the problem -abu+bou+cu=f., u=0 ondor I prove atu, ul conts. @ if Blu,v) = (b. 14, U) + ((4,0) prove that B244) = ((c- — ob)4;4) ③if c±vbo prove that acuius v. elliptic.
Q3: Define the linear functional J: H₁(2) R by ¡(v) = a(v, v) - L(v) Л Let u be the unique weak solution to a(u,v) = L(v) in H(2) and suppose that a(...) is a symmetric bilinear form on H(2) prove that 1- u is minimizer. 2- u is unique. 3- The minimizer J(u) can be rewritten under 1(u) = u Au-ub, algebraic form 1 2 Where A, b are repictively the stiffence matrix and the load vector Q4: A) Answer 1- show that the solution to -Au = f in A, u = 0 on a satisfies the stability Vullfll and show that ||V(u u)||||||2 - ||vu||2 2- Prove that Where lu-ul Chuz - !ull = a(u, u) = Vu. Vu dx + fu. uds B) Consider the bilinea forta Л a(u, v) = (Au, Av) (Vu, Vv + (Vu, v) + (u,v) Show that a(u, v) continues and V- elliptic on H(2)
7) In the diagram below of quadrilateral ABCD, E and F are points on AB and CD respectively, BE=DF, and AE = CF. Which conclusion can be proven? A 1) ED = FB 2) AB CD 3) ZA = ZC 4) ZAED/CFB E B D 0

Chapter 3 Solutions

Elementary Geometry For College Students, 7e

Ch. 3.1 - In Exercises 1 to 4, consider the congruent...Ch. 3.1 - In Exercises 1 to 4. consider the congruent...Ch. 3.1 - In Exercises 1 to 4. consider the congruent...Ch. 3.1 - In Exercises 1 to 4, consider the congruent...Ch. 3.1 - Consider ABC and ABD in the figure shown. By the...Ch. 3.1 - In a right triangle, the sides that form the right...Ch. 3.1 - In ABC, the midpoints of the sides are joined. a...Ch. 3.1 - a. Suppose that you wish to prove that RSTSRV....Ch. 3.1 - In Exercises 9 to 12, congruent parts are...Ch. 3.1 - In Exercises 9 to 12, congruent parts are...
Ch. 3.1 - In Exercises 9 to 12, congruent parts are...Ch. 3.1 - In Exercises 9 to 12, congruent parts are...Ch. 3.1 - In Exercises 13 to 18, use only the given...Ch. 3.1 - In Exercises 13 to 18, use only the given...Ch. 3.1 - In Exercises 13 to 18, use only the given...Ch. 3.1 - In Exercises 13 to 18, use only the given...Ch. 3.1 - In Exercises 13 to 18, use only the given...Ch. 3.1 - In Exercises 13 to 18, use only the given...Ch. 3.1 - In Exercises 19 and 20, the triangles to be proved...Ch. 3.1 - In Exercises 19 and 20, the triangles to be proved...Ch. 3.1 - In Exercises 21 to 24, the triangles named can be...Ch. 3.1 - In Exercises 21 to 24, the triangles named can be...Ch. 3.1 - In Exercises 21 to 24, the triangles named can be...Ch. 3.1 - In Exercises 21 to 24, the triangles named can be...Ch. 3.1 - In Exercises 25 and 26, complete each proof. Use...Ch. 3.1 - In Exercises 25 and 26, complete each proof. Use...Ch. 3.1 - In Exercises 27 to 32, use SSS, SAS, ASA, or AAS...Ch. 3.1 - In Exercises 27 to 32, use SSS, SAS, ASA, or AAS...Ch. 3.1 - In Exercises 27 to 32, use SSS, SAS, ASA, or AAS...Ch. 3.1 - In Exercises 27 to 32, use SSS, SAS, ASA, or AAS...Ch. 3.1 - In Exercises 27 to 32, use SSS, SAS, ASA, or AAS...Ch. 3.1 - In Exercises 27 to 32, use SSS, SAS, ASA, or AAS...Ch. 3.1 - In Exercises 33 to 36, the methods to be used are...Ch. 3.1 - In Exercises 33 to 36, the methods to be used are...Ch. 3.1 - In Exercises 33 to 36, the method to be used are...Ch. 3.1 - In Exercises 33 to 36, the method to be used are...Ch. 3.1 - In quadrilateral ABCD, AC and BD are perpendicular...Ch. 3.1 - In ABC and DEF, you know that AD, CF, and ABDE....Ch. 3.1 - Are quadrilaterals ABCD and EFGH congruent if: a...Ch. 3.1 - Are quadrilaterals ABCD and EFGH congruent if: a...Ch. 3.1 - In Exercises 41 to 42, complete each proof. Given:...Ch. 3.1 - In Exercises 41 to 42, complete each proof. Given:...Ch. 3.1 - Given: ABC; RS is the perpendicular bisector of...Ch. 3.2 - In Exercises 1 to 4, state the reason SSS, SAS,...Ch. 3.2 - In Exercises 1 to 4, state the reason SSS, SAS,...Ch. 3.2 - In Exercises 1 to 4, state the reason SSS, SAS,...Ch. 3.2 - In Exercises 1 to 4, state the reason SSS, SAS,...Ch. 3.2 - In Exercise 5 to 12, plan and write the two-column...Ch. 3.2 - In Exercise 5 to 12, plan and write the two-column...Ch. 3.2 - In Exercise 5 to 12, plan and write the two-column...Ch. 3.2 - In Exercise 5 to 12, plan and write the two-column...Ch. 3.2 - Prob. 9ECh. 3.2 - In Exercise 5 to 12, plan and write the two-column...Ch. 3.2 - In Exercise 5 to 12, plan and write the two-column...Ch. 3.2 - In Exercise 5 to 12, plan and write the two-column...Ch. 3.2 - Prob. 13ECh. 3.2 - Prob. 14ECh. 3.2 - Given: HJ bisects KHL HJKL Prove: KL PROOF...Ch. 3.2 - Given: HJ bisects KHL HJKL In Exercise 15, you cam...Ch. 3.2 - In Exercise 17 to 20, first prove that triangles...Ch. 3.2 - In Exercise 17 to 20, first prove that triangles...Ch. 3.2 - In Exercise 17 to 20, first prove that triangles...Ch. 3.2 - In Exercise 17 to 20, first prove that triangles...Ch. 3.2 - In Exercise 21 to 26, ABC is a right triangle. Use...Ch. 3.2 - In Exercise 21 to 26, ABC is a right triangle. Use...Ch. 3.2 - In Exercise 21 to 26, ABC is a right triangle. Use...Ch. 3.2 - In Exercise 21 to 26, ABC is a right triangle. Use...Ch. 3.2 - In Exercise 21 to 26, ABC is a right triangle. Use...Ch. 3.2 - In Exercise 21 to 26, ABC is a right triangle. Use...Ch. 3.2 - In Exercise 27 to 29, prove the indicated...Ch. 3.2 - In Exercise 27 to 29, prove the indicated...Ch. 3.2 - In Exercise 27 to 29, prove the indicated...Ch. 3.2 - In Exercise 30 to 32, draw the triangle that is to...Ch. 3.2 - Prob. 31ECh. 3.2 - In Exercises 30 to 32, draw the triangles that are...Ch. 3.2 - Given: RW bisects SRU Prove: RSRU TRUVRS HINT:...Ch. 3.2 - Given: DBBC and CEDE Prove: ABAE BDCECD HINT:...Ch. 3.2 - In the roof truss shown, AB=8 and mHAF=37. Find: a...Ch. 3.2 - In the support system of the bridge shown, AC=6ft...Ch. 3.2 - As a car moves along A section of the roadway in a...Ch. 3.2 - Because of the construction along the road from A...Ch. 3.2 - Prob. 39ECh. 3.2 - As marked and with HC, a are quadrilateral ABCD...Ch. 3.2 - Given: Regular pentagon ABCDE with diagonals BE...Ch. 3.2 - In the figure with regular pentagon ABCDE, do BE...Ch. 3.2 - Prob. 43ECh. 3.2 - HA hypotenuse-angle is also a valid method for...Ch. 3.2 - Prob. 45ECh. 3.3 - For Exercises 1 to 10, use the accompanying...Ch. 3.3 - For Exercises 1 to 10, use the accompanying...Ch. 3.3 - Prob. 3ECh. 3.3 - For Exercises 1 to 10, use the accompanying...Ch. 3.3 - For Exercises 1 to 10, use the accompanying...Ch. 3.3 - For Exercises 1 to 10, use the accompanying...Ch. 3.3 - For Exercises 1 to 10, use the accompanying...Ch. 3.3 - For Exercises 1 to 10, use the accompanying...Ch. 3.3 - Prob. 9ECh. 3.3 - For Exercises 1 to 10, use the accompanying...Ch. 3.3 - In Exercises 11 to 14, determine whether the sets...Ch. 3.3 - In Exercises 11 to 14, determine whether the sets...Ch. 3.3 - In Exercises 11 to 14, determine whether the sets...Ch. 3.3 - In Exercises 11 to 14, determine whether the sets...Ch. 3.3 - Prob. 15ECh. 3.3 - Prob. 16ECh. 3.3 - In Exercises 15 to 20, describe the line segments...Ch. 3.3 - Prob. 18ECh. 3.3 - Prob. 19ECh. 3.3 - Prob. 20ECh. 3.3 - Prob. 21ECh. 3.3 - Is it possible for a triangle to be: a an acute...Ch. 3.3 - A surveyor knows that a lot has the shape of an...Ch. 3.3 - In concave quadrilateral ABCD, the angle at A...Ch. 3.3 - Prob. 25ECh. 3.3 - Prob. 26ECh. 3.3 - Prob. 27ECh. 3.3 - Prob. 28ECh. 3.3 - Prob. 29ECh. 3.3 - Prob. 30ECh. 3.3 - Prob. 31ECh. 3.3 - In Exercises 31 to 34, suppose that BC is the base...Ch. 3.3 - In Exercises 31 to 34, suppose that BC is the base...Ch. 3.3 - Prob. 34ECh. 3.3 - Suppose that ABCDEF. Also, AX bisects CAB and DY...Ch. 3.3 - Suppose that ABCDEF. Also, AX is the median from A...Ch. 3.3 - In Exercises 37 and 38 , complete each proof using...Ch. 3.3 - In Exercises 37 and 38 , complete each proof using...Ch. 3.3 - Prob. 39ECh. 3.3 - In Exercises 39 to 41, complete each proof. Given:...Ch. 3.3 - In Exercises 39 to 41, complete each proof. Given:...Ch. 3.3 - Prob. 42ECh. 3.3 - Prob. 43ECh. 3.3 - In PMN, PMPN, MB bisects PMN and NA bisects PNM....Ch. 3.3 - ABC lies in the structural support system of the...Ch. 3.3 - In Exercises 46 to 48, explain why each statement...Ch. 3.3 - Prob. 47ECh. 3.3 - Prob. 48ECh. 3.3 - Prob. 49ECh. 3.3 - Given : In the figure, a=e=66. Also, YZZW. If...Ch. 3.4 - In Exercises 1 to 6, use line segments of given...Ch. 3.4 - Prob. 2ECh. 3.4 - Prob. 3ECh. 3.4 - Prob. 4ECh. 3.4 - Prob. 5ECh. 3.4 - Prob. 6ECh. 3.4 - Prob. 7ECh. 3.4 - Prob. 8ECh. 3.4 - Prob. 9ECh. 3.4 - Prob. 10ECh. 3.4 - Prob. 11ECh. 3.4 - Prob. 12ECh. 3.4 - In Exercises 13 and 14. use the angles and lengths...Ch. 3.4 - Prob. 14ECh. 3.4 - Prob. 15ECh. 3.4 - Prob. 16ECh. 3.4 - Prob. 17ECh. 3.4 - Prob. 18ECh. 3.4 - Prob. 19ECh. 3.4 - Prob. 20ECh. 3.4 - Prob. 21ECh. 3.4 - Prob. 22ECh. 3.4 - In Exercises 23 to 26, use line segments of length...Ch. 3.4 - Prob. 24ECh. 3.4 - In Exercises 23 to 26, use line segments of length...Ch. 3.4 - Prob. 26ECh. 3.4 - In Exercise 27 and 28, use the given angle R and...Ch. 3.4 - Prob. 28ECh. 3.4 - Complete the justification of the construction of...Ch. 3.4 - Prob. 30ECh. 3.4 - Prob. 31ECh. 3.4 - Prob. 32ECh. 3.4 - Prob. 33ECh. 3.4 - Prob. 34ECh. 3.4 - Prob. 35ECh. 3.4 - Draw a right triangle and construct the angle...Ch. 3.4 - Draw an obtuse triangle and construct the three...Ch. 3.4 - Prob. 38ECh. 3.4 - A carpenter has placed a square over an angle in...Ch. 3.4 - Prob. 40ECh. 3.5 - In Exercise 1 to 10, classify each statement as...Ch. 3.5 - In Exercise 1 to 10, classify each statement as...Ch. 3.5 - In Exercise 1 to 10, classify each statement as...Ch. 3.5 - In Exercise 1 to 10, classify each statement as...Ch. 3.5 - In Exercise 1 to 10, classify each statement as...Ch. 3.5 - In Exercise 1 to 10, classify each statement as...Ch. 3.5 - In Exercise 1 to 10, classify each statement as...Ch. 3.5 - In Exercise 1 to 10, classify each statement as...Ch. 3.5 - In Exercise 1 to 10, classify each statement as...Ch. 3.5 - In Exercise 1 to 10, classify each statement as...Ch. 3.5 - Is it possible to draw a triangle whose angles...Ch. 3.5 - Is it possible to draw a triangle whose angles...Ch. 3.5 - Is it possible to draw a triangle whose sides...Ch. 3.5 - Is it possible to draw a triangle whose sides...Ch. 3.5 - Prob. 15ECh. 3.5 - In Exercises 15 to 18, describe the triangle XYZ ,...Ch. 3.5 - Prob. 17ECh. 3.5 - In Exercises 15 to 18, describe the triangle XYZ ,...Ch. 3.5 - Two of the sides of an isosceles triangle have...Ch. 3.5 - The sides of a right triangle have lengths of 6cm,...Ch. 3.5 - Prob. 21ECh. 3.5 - One of the angles of an isosceles triangle...Ch. 3.5 - An auto parts dealer in Huntsville, Alabama at...Ch. 3.5 - A tornado has just struck a small Kansas community...Ch. 3.5 - In Exercises 25 and 26, complete each proof....Ch. 3.5 - Prob. 26ECh. 3.5 - In Exercises 27 and 28, construct proofs. Given:...Ch. 3.5 - In Exercises 27 and 28, construct proofs. Given:...Ch. 3.5 - Prob. 29ECh. 3.5 - In MNP not shown, point Q lies on NP so that MQ...Ch. 3.5 - In Exercises 31 to 34, apply a form of Theorem...Ch. 3.5 - In Exercises 31 to 34, apply a form of Theorem...Ch. 3.5 - Prob. 33ECh. 3.5 - In Exercises 31 to 34, apply a form of Theorem...Ch. 3.5 - Prove by the indirect method: Given: MPN is not...Ch. 3.5 - Prove by the indirect method: Given: Scalene XYZ...Ch. 3.5 - In Exercises 37 and 38, prove each theorem. The...Ch. 3.5 - In Exercises 37 and 38, prove each theorem. The...Ch. 3.5 - Prob. 39ECh. 3.5 - In isosceles MNP, MNMP. With point Q on MN,...Ch. 3.CR - Given: AEBDEC AEDE Prove: AEBDECCh. 3.CR - Given: ABEFACDF12 Prove: BECh. 3.CR - Given: AD bisects BC ABBCDCBC Prove: AEDECh. 3.CR - Prob. 4CRCh. 3.CR - Prob. 5CRCh. 3.CR - Given: B is the midpoint of AC BDAC Prove: ADC is...Ch. 3.CR - Prob. 7CRCh. 3.CR - Prob. 8CRCh. 3.CR - Given: YZ is the base of an isosceles triangle;...Ch. 3.CR - Prob. 10CRCh. 3.CR - Prob. 11CRCh. 3.CR - Prob. 12CRCh. 3.CR - Given: ABCDBADCDA Prove: AED is isosceles HINT:...Ch. 3.CR - Given: AC bisects BAD Prove: ADCDCh. 3.CR - Prob. 15CRCh. 3.CR - Prob. 16CRCh. 3.CR - Prob. 17CRCh. 3.CR - Name the longest line segment shown in...Ch. 3.CR - Prob. 19CRCh. 3.CR - Two sides of a triangle have lengths 15 and 20....Ch. 3.CR - Prob. 21CRCh. 3.CR - Prob. 22CRCh. 3.CR - Prob. 23CRCh. 3.CR - Prob. 24CRCh. 3.CR - Given: ABC is isosceles with base AB...Ch. 3.CR - Prob. 26CRCh. 3.CR - Prob. 27CRCh. 3.CR - Construct a right triangle that has acute angle A...Ch. 3.CR - Prob. 29CRCh. 3.CT - It is given that ABCDEF triangles not shown a If...Ch. 3.CT - 2. Consider XYZ triangles not shown a Which side...Ch. 3.CT - 3. State the reason SSS, SAS, ASA, AAS, or HL why...Ch. 3.CT - Write the statement that is represented by the...Ch. 3.CT - 5. With congruent parts marked, are the two...Ch. 3.CT - With ABDCBE and A-D-E-C, does it necessarily...Ch. 3.CT - Prob. 7CTCh. 3.CT - CM is the median for ABC from vertex C to side AB....Ch. 3.CT - Prob. 9CTCh. 3.CT - In TUV, TU. Exercises 9, 10 a If VT=7.6inches and...Ch. 3.CT - Prob. 11CTCh. 3.CT - Show all arcs in the following construction....Ch. 3.CT - Prob. 13CTCh. 3.CT - In TUV not shown, TUTVVU. Write a three-part...Ch. 3.CT - In the figure, A is the right angle,...Ch. 3.CT - Prob. 16CTCh. 3.CT - Complete all statements and reasons for the...Ch. 3.CT - Complete all missing statements and reasons in the...Ch. 3.CT - The perimeter of an isosceles triangle is 32cm. If...
Knowledge Booster
Background pattern image
Geometry
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Text book image
Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning
SEE MORE TEXTBOOKS
What are the Different Types of Triangles? | Don't Memorise; Author: Don't Memorise;https://www.youtube.com/watch?v=1k0G-Y41jRA;License: Standard YouTube License, CC-BY
Law of Sines AAS, ASA, SSA Ambiguous Case; Author: Mario's Math Tutoring;https://www.youtube.com/watch?v=FPVGb-yWj3s;License: Standard YouTube License, CC-BY
Introduction to Statistics..What are they? And, How Do I Know Which One to Choose?; Author: The Doctoral Journey;https://www.youtube.com/watch?v=HpyRybBEDQ0;License: Standard YouTube License, CC-BY
Triangles | Mathematics Grade 5 | Periwinkle; Author: Periwinkle;https://www.youtube.com/watch?v=zneP1Q7IjgQ;License: Standard YouTube License, CC-BY
What Are Descriptive Statistics And Inferential Statistics?; Author: Amour Learning;https://www.youtube.com/watch?v=MUyUaouisZE;License: Standard Youtube License