
Concept explainers
Mixtures Solely on the basis of the physical description of the mixture problem on page 108 and in Figure 3.3.1, discuss the nature of the functions x1(t) and x2(t). What is the behavior of each function over a long period of time? Sketch possible graphs of x1(t) and x2(t). Check your conjectures by using a numerical solver to obtain numerical solution curves of (3) subject to the initial conditions x1(0) = 25, x1(0) = 0.
MIXTURES Consider the two tanks shown in Figure 3.3.1. Let us suppose for the sake of discussion that tank A contains 50 gallons of water in which 25 pounds of salt is dissolved. Suppose tank B contains 50 gallons of pure water. Liquid is pumped into and out of the tanks as indicated in the figure; the mixture exchanged between the two tanks and the liquid pumped out of tank B are assumed to be well stirred. We wish to construct a mathematical model that describes the number of pounds x1(t) and x2(t) of salt in tanks A and B, respectively, at time t.
Figure 3.3.1 Connected mixing tanks
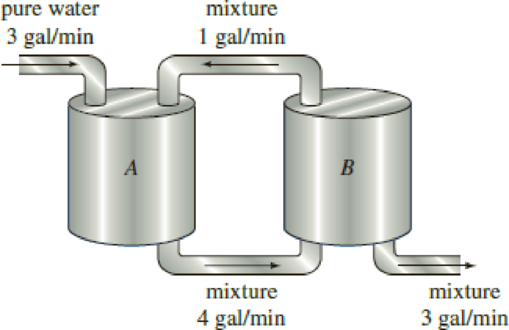
dx1dt=−225x1+150x2dx2dt= 225x1−225x2. (3)
Trending nowThis is a popular solution!

Chapter 3 Solutions
Differential Equations with Boundary-Value Problems (MindTap Course List)
- 1. Given that h(t) = -5t + 3 t². A tangent line H to the function h(t) passes through the point (-7, B). a. Determine the value of ẞ. b. Derive an expression to represent the gradient of the tangent line H that is passing through the point (-7. B). c. Hence, derive the straight-line equation of the tangent line H 2. The function p(q) has factors of (q − 3) (2q + 5) (q) for the interval -3≤ q≤ 4. a. Derive an expression for the function p(q). b. Determine the stationary point(s) of the function p(q) c. Classify the stationary point(s) from part b. above. d. Identify the local maximum of the function p(q). e. Identify the global minimum for the function p(q). 3. Given that m(q) = -3e-24-169 +9 (-39-7)(-In (30-755 a. State all the possible rules that should be used to differentiate the function m(q). Next to the rule that has been stated, write the expression(s) of the function m(q) for which that rule will be applied. b. Determine the derivative of m(q)arrow_forwardPlease help me organize the proof of the following theorem:arrow_forwardThe population mean and standard deviation are given below. Find the required probability and determine whether the given sample mean would be considered unusual. For a sample of n = 65, find the probability of a sample mean being greater than 225 if μ = 224 and σ = 3.5. For a sample of n = 65, the probability of a sample mean being greater than 225 if μ=224 and σ = 3.5 is 0.0102 (Round to four decimal places as needed.)arrow_forward
- uestion 10 of 12 A Your answer is incorrect. L 0/1 E This problem concerns hybrid cars such as the Toyota Prius that are powered by a gas-engine, electric-motor combination, but can also function in Electric-Vehicle (EV) only mode. The figure below shows the velocity, v, of a 2010 Prius Plug-in Hybrid Prototype operating in normal hybrid mode and EV-only mode, respectively, while accelerating from a stoplight. 1 80 (mph) Normal hybrid- 40 EV-only t (sec) 5 15 25 Assume two identical cars, one running in normal hybrid mode and one running in EV-only mode, accelerate together in a straight path from a stoplight. Approximately how far apart are the cars after 15 seconds? Round your answer to the nearest integer. The cars are 1 feet apart after 15 seconds. Q Search M 34 mlp CHarrow_forwardFind the volume of the region under the surface z = xy² and above the area bounded by x = y² and x-2y= 8. Round your answer to four decimal places.arrow_forwardУ Suppose that f(x, y) = · at which {(x, y) | 0≤ x ≤ 2,-x≤ y ≤√x}. 1+x D Q Then the double integral of f(x, y) over D is || | f(x, y)dxdy = | Round your answer to four decimal places.arrow_forward
- D The region D above can be describe in two ways. 1. If we visualize the region having "top" and "bottom" boundaries, express each as functions of and provide the interval of x-values that covers the entire region. "top" boundary 92(x) = | "bottom" boundary 91(x) = interval of values that covers the region = 2. If we visualize the region having "right" and "left" boundaries, express each as functions of y and provide the interval of y-values that covers the entire region. "right" boundary f2(y) = | "left" boundary fi(y) =| interval of y values that covers the region =arrow_forwardFind the volume of the region under the surface z = corners (0,0,0), (2,0,0) and (0,5, 0). Round your answer to one decimal place. 5x5 and above the triangle in the xy-plane witharrow_forwardGiven y = 4x and y = x² +3, describe the region for Type I and Type II. Type I 8. y + 2 -24 -1 1 2 2.5 X Type II N 1.5- x 1- 0.5 -0.5 -1 1 m y -2> 3 10arrow_forward
- Given D = {(x, y) | O≤x≤2, ½ ≤y≤1 } and f(x, y) = xy then evaluate f(x, y)d using the Type II technique. 1.2 1.0 0.8 y 0.6 0.4 0.2 0- -0.2 0 0.5 1 1.5 2 X X This plot is an example of the function over region D. The region identified in your problem will be slightly different. y upper integration limit Integral Valuearrow_forwardThis way the ratio test was done in this conflicts what I learned which makes it difficult for me to follow. I was taught with the limit as n approaches infinity for (an+1)/(an) = L I need to find the interval of convergence for the series tan-1(x2). (The question has a table of Maclaurin series which I followed as well) https://www.bartleby.com/solution-answer/chapter-92-problem-7e-advanced-placement-calculus-graphical-numerical-algebraic-sixth-edition-high-school-binding-copyright-2020-6th-edition/9781418300203/2c1feea0-c562-4cd3-82af-bef147eadaf9arrow_forwardSuppose that f(x, y) = y√√r³ +1 on the domain D = {(x, y) | 0 ≤y≤x≤ 1}. D Then the double integral of f(x, y) over D is [ ], f(x, y)dzdy =[ Round your answer to four decimal places.arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
