
Repeat Example 31.1, but for
To calculate: The solution to the Poisson’s equation
Answer to Problem 1P
Solution: Solution to the Poisson’s equation for provided boundary equation is
Explanation of Solution
Given Information:
Poisson’s equation:
Here, function
Boundary conditions are as
The value of the uniform heat source is
Formula used:
If a differential is in the form
Calculation:
Consider the problem statement, the expression for the boundary condition is:
The Boundary condition is provided as follows:
The general solution to the differential equation is:
Differentiate it with respect to
Compares the equations with each other.
Apply the boundary condition
Apply the boundary condition
Substitute
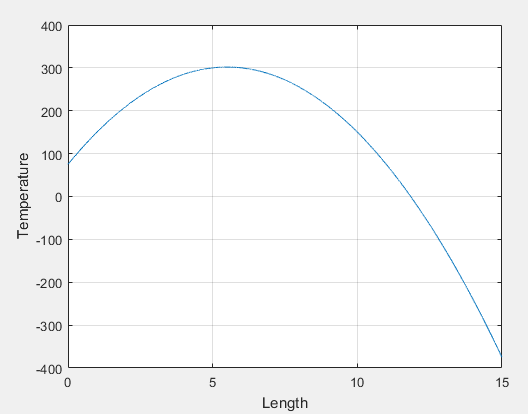
Use the following MATLAB command to execute the code and plot the temperature as a function of position along the rod.
Now, execute the program by pressing run button. Following plot is obtained that shows the plot of temperature verses distance.
Want to see more full solutions like this?
Chapter 31 Solutions
EBK NUMERICAL METHODS FOR ENGINEERS
- An electric heater with a capacity P is used to heat air in a spherical chamber. The inside radius is r. outside radius r, and the conductivity is k. surface heat is exchanged by convection. Sur At the inside kh The inside heat transfer coefficient is h,. Heat loss from the outside surface is by +1 radiation. The surroundings temperature is Tur and the surface emissivity is ɛ. Assuming one-dimensional steady state conduction, use a simplified radiation model to determine: [a] The temperature distribution in the spherical wall. [b] The inside air temperatures for the following conditions: h-6.5 W/m-"C, P-1, 500 W, &=0.81, T 18°C. %3D sur k 2.4 W/m-°C. 1=10 cm. 1,= 14 cm.arrow_forwardEstimate the heat exchanger area needed to cool 55,000 lb/hr of a light oil (specific heat= 0.74 Btu/lb°F) from 190°F to 140°F using cooling water that is available at 50°F. Thecooling water can be allowed to heat to 90°F. An initial estimate of the Overall HeatTransfer Coefficient is 120 Btu/hr.ft².°F. Show a schematic of the heat exchanger. Estimate the required mass flow rate of cooling water. The LMTD Taking the shell and tube heat exchanger described above how manytubes of 3 inch diameter and 10 ft length should be used?arrow_forwardQi: (50 marks) Find the total heat flux of the composite wall when: B KA = KC = KF = 15 m. K KB = KD = 10 m. K KE = KG = 20 %3D m. K D. Height of B = C = D 4 cm 3 cm 4 cm 6 cm Height of F = G AT = 30 Karrow_forward
- 5.72 A cold air chamber is proposed for quenching steel ball bearings of diameter D = 0.2 m and initial temperature T₁ = 400°C. Air in the chamber is maintained at -15°C by a refrigeration system, and the steel balls pass through the chamber on a conveyor belt. Optimum bearing production requires that 70% of the initial ther- mal energy content of the ball above -15°C be removed. Radiation effects may be neglected, and the convection heat transfer coefficient within the chamber is 1000 W/m².K. Estimate the residence time of the balls within the chamber, and recommend a drive veloc- ity of the conveyor. The following properties may be used for the steel: k = 50 W/m K, a = 2 x 105 m²/s, and c = 450 J/kg.K. Ball bearing -5 m Cold air Belt V Chamber housingarrow_forwardProblem 5. Heat is generated uniformly at a rate of Se in a copper wire of radius re having thermal conductivity k where the ambient temperature is T. and the heat transfer coefficient is ho. At steady state; i. ii. iii. find an expression for the temperature distribution at steady-state and draw a T vs. r graph. Substituting; S₂ = 125 kW/m³, k = 390 W/m.K, rc = 2 mm, T = 20°C and hoc=25W/m²K, find the steady state surface and center temperatures and the heat transfer rate to the surroundings. Repeat part i and ii when the wire is covered with an insulation of thickness ti and ki which are 0.1 mm and 0.2 W/m.K, respectively.arrow_forwardA 200cc single-cylinder gasoline engine used as a prime mover in a motorcycle bike has a clearance volume of 12cc. If the heat addition rate is 12kW, determine the output shaft power that could be derived in the engine. Assume an air standard analysis during computation.a. 8.1952kW b. 8.1951kW c. 8.1953kW d. 8.1954kWarrow_forward
- In any heat exchanger, the log mean temperature difference "could" be the same as the mean "average" temperature difference of both ends of the heat exchanger, depending on the temperature profile within that heat exchanger along heat exchanger tubes. Select one: OTrue O False At very low pressures (vacuum), the thermal conductivity of gases approaches zero. Select one: O True O Falsearrow_forwardQ4. Calculate the minimum heat flux using an energy balance at the material surface and the time-to-ignition if the ignition temperature is 150 "C, ambient temperature is 30 "C. The thermal properties of aluminium alloy balls ( K- 4.8 W/m.K, C, 950 J/kg.K, 2770 kg/m. The emissivity to the surface is 0.8, Stefan Boltzman constant is 5.67x10 W/m.K. Convictive heat transfer coefficient is 12 W/m'K and net heat flux into the material surface is 20 KW/m.arrow_forwardRefrigerant condenses in the tubes of a cross flow heat exchanger at 41 °C, 16.7 MJ/hr is rejected form the refrigerant by air "c= 1005 J/kg.K". Air enters at 24 °C and leaves at 37 ;c. What is heat transfer area of the refrigerant side (m) when the overall heat transfer coefficient refrigerant side on the is 151 W/m".°C? Hint use LMTD method and assume a correction coefficient of 100%arrow_forward
- For Heat transfer through cylinder tube wall, the temperature is to be a linear function of r (radius) of the tube. Select one: O True O False The conductivity of H20 in solid form (ice) is higher than that of H20 in liquid form (water). Select one: O True O False F, (Correction factor for temperature in some heat exchangers) should be 1.0 or greater than 1.0 in some cases. Select one: O True Falsearrow_forwardThe pressurized water that enters a cross-flow heat exchanger with a flow of 1 kg / s at 35 ° C and leaves at 125 ° C, where fluids do not mix, is heated by exhaust gases entering the heat exchanger at 300 ° C and exiting at 100 ° C. . The total heat transfer coefficient defined according to the surface on the gas side is 100 W / m ° K. Thermal properties of exhaust gases are considered as atmospheric air. a) Find the required surface area on the gas side. (15P) Due to the contamination that occurs over time, the inlet temperature and flow rate of the water in the heat exchanger remain the same, while the outlet temperature drops to 105 ° C *.a) Calculate the new condition with the acceptance of fixed thermal properties, b) Heat transfer, c) Exhaust gases exit temperature.arrow_forwardAnswer this using 7 steps below: GIVEN: REQUIRED: ASSUMPTION: ILLUSTRATION: FOMULA: SOLUTION: ANSWER:arrow_forward
 Principles of Heat Transfer (Activate Learning wi...Mechanical EngineeringISBN:9781305387102Author:Kreith, Frank; Manglik, Raj M.Publisher:Cengage Learning
Principles of Heat Transfer (Activate Learning wi...Mechanical EngineeringISBN:9781305387102Author:Kreith, Frank; Manglik, Raj M.Publisher:Cengage Learning
