Videos
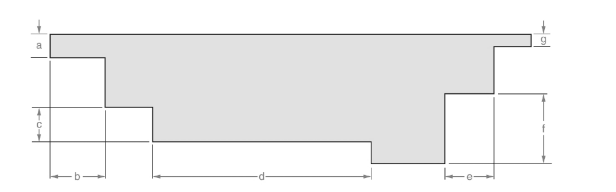
(a)
Measure the length for dimension (a).
Answer to Problem 13A
The measurement of the length is 14′′.
Explanation of Solution
Given:
The line is given below:
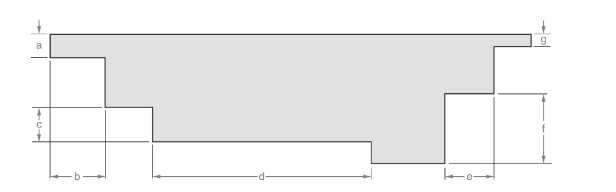
Concept used:
Length is measured with the help of inch scale.
Calculation:
Attached the inch scale over given length.
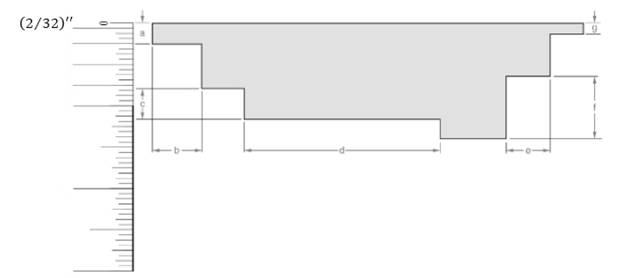
From the above figure, the length of the line can be measured as follows:
La=8(132)′′La=14′′
Thus, the measurement of the length is 14′′.
Conclusion:
The measurement of the length is 14′′.
(b)
Measure the length for dimension (b).
Answer to Problem 13A
The measurement of the length is 58′′.
Explanation of Solution
Given:
The line is given below:
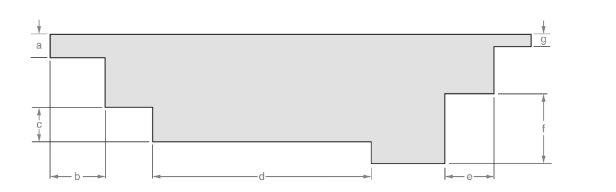
Concept used:
Length is measured with the help of inch scale.
Calculation:
Attached the inch scale over given length.
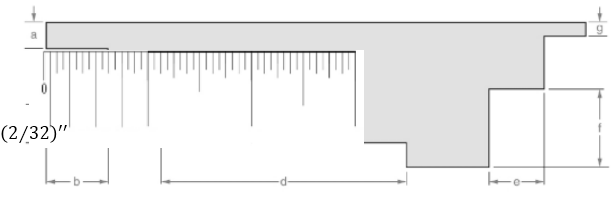
From the above figure, the length of the line can be measured as follows:
L=10(132)′′L=58′′
Thus, the measurement of the length is 58′′.
Conclusion:
The measurement of the length is 58′′.
(c)
Measure the length for dimension (c).
Answer to Problem 13A
The measurement of the length is 58′′.
Explanation of Solution
Given:
The line is given below:
Concept used:
Length is measured with the help of inch scale.
Calculation:
Attached the inch scale over given length.
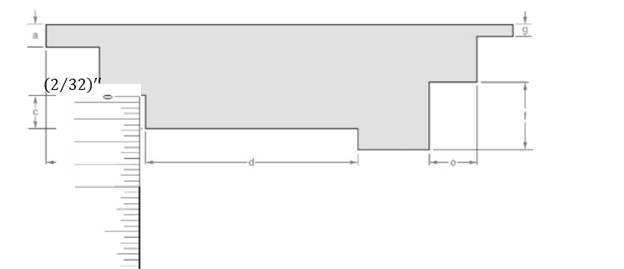
From the above figure, the length of the line can be measured as follows:
Lc=11(132)′′Lc=1132′′
Thus, the measurement of the length is 1132′′.
Conclusion:
The measurement of the length is 1132′′.
(d)
Measure the length for dimension (d).
Answer to Problem 13A
The measurement of the length is 2732′′.
Explanation of Solution
Given:
The line is given below:
Concept used:
Length is measured with the help of inch scale.
Calculation:
Attached the inch scale over given length.
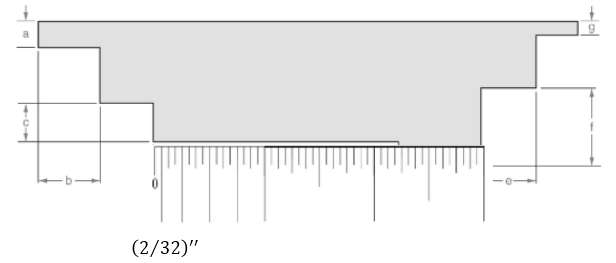
From the above figure, the length of the line can be measured as follows:
L=2″+7(132)′′L=2732′′
Thus, the measurement of the length is 2732′′.
Conclusion:
The measurement of the length is 2732′′.
(e)
Measure the length for dimension (e).
Answer to Problem 13A
The measurement of the length is 12′′.
Explanation of Solution
Given:
The line is given below:
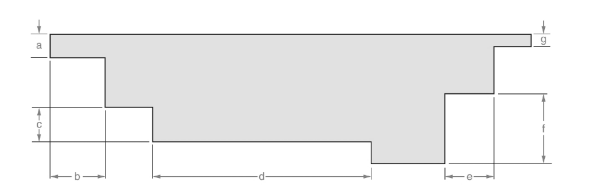
Concept used:
Length is measured with the help of inch scale.
Calculation:
Attached the inch scale over given length.
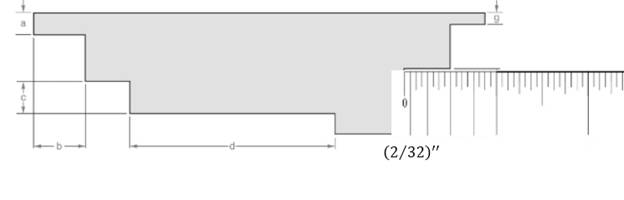
From the above figure, the length of the line can be measured as follows:
L=16(132)′′L=12′′
Thus, the measurement of the length is 12′′.
Conclusion:
The measurement of the length is 12′′.
(f)
Measure the length for dimension (f).
Answer to Problem 13A
The measurement of the length is 2332′′.
Explanation of Solution
Given:
The line is given below:
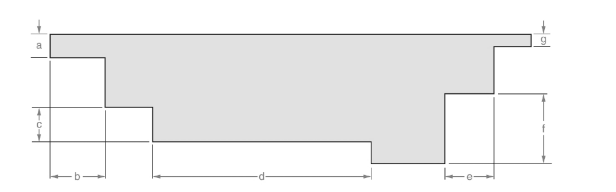
Concept used:
Length is measured with the help of inch scale.
Calculation:
Attached the inch scale over given length.
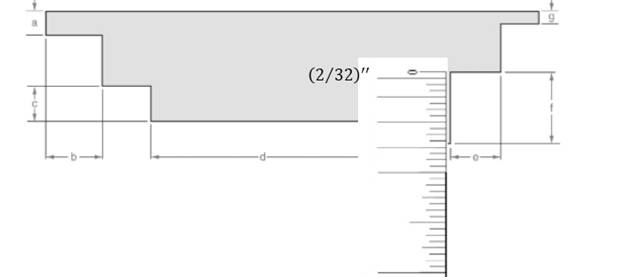
From the above figure, the length of the line can be measured as follows:
L=23(132)′′L=2332′′
Thus, the measurement of the length is 2332′′.
Conclusion:
The measurement of the length is 2332′′.
(g)
Measure the length for dimension (g).
Answer to Problem 13A
The measurement of the length is 532′′.
Explanation of Solution
Given:
The line is given below:
Concept used:
Length is measured with the help of inch scale.
Calculation:
Attached the inch scale over given length.
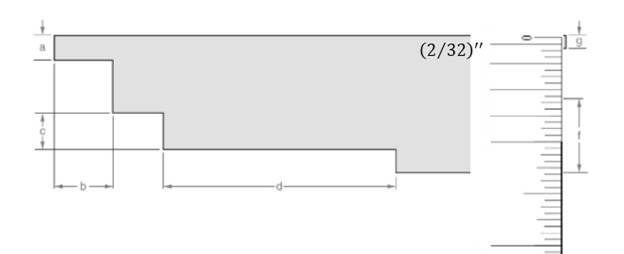
From the above figure, the length of the line can be measured as follows:
L=5(132)′′L=532′′
Thus, the measurement of the length is 532′′.
Conclusion:
The measurement of the length is 532′′.
Want to see more full solutions like this?
Chapter 30 Solutions
EBK MATHEMATICS FOR MACHINE TECHNOLOGY
- In Exercises 1-14, state whether each statement is true or false. If false, give a reason. 1. The set of stores located in the state of Wyoming is a well- defined set. 2. The set of the three best songs is a well-defined set. 3. maple = {oak, elm, maple, sycamore} 4{} cơ 5. {3, 6, 9, 12,...} and {2, 4, 6, 8, ...} are disjoint sets. 6. {Mercury, Venus, Earth, Mars} is an example of a set in roster form. 7. {candle, picture, lamp} = {picture, chair, lamp } 8. {apple, orange, banana, pear} is equivalent to {tomato, corn, spinach, radish}.arrow_forwardExercises Evaluate the following limits. 1. lim cot x/ln x +01x 2. lim x² In x +014 3. lim x* x0+ 4. lim (cos√√x)1/x +014 5. lim x2/(1-cos x) x10 6. lim e*/* 818 7. lim (secx - tan x) x-x/2- 8. lim [1+(3/x)]* x→∞0arrow_forwardIn Exercises 1 through 3, let xo = O and calculate P7(x) and R7(x). 1. f(x)=sin x, x in R. 2. f(x) = cos x, x in R. 3. f(x) = In(1+x), x≥0. 4. In Exercises 1, 2, and 3, for |x| 1, calculate a value of n such that P(x) approximates f(x) to within 10-6. 5. Let (an)neN be a sequence of positive real numbers such that L = lim (an+1/an) exists in R. If L < 1, show that an → 0. [Hint: Let 1111 Larrow_forward
- iation 7. Let f be continuous on [a, b] and differentiable on (a, b). If lim f'(x) xia exists in R, show that f is differentiable at a and f'(a) = lim f'(x). A similar result holds for b. x-a 8. In reference to Corollary 5.4, give an example of a uniformly continuous function on [0, 1] that is differentiable on (0, 1] but whose derivative is not bounded there. 9. Recall that a fixed point of a function f is a point c such that f(c) = c. (a) Show that if f is differentiable on R and f'(x)| x if x 1 and hence In(1+x) 0. 12. For 0 л/2. (Thus, as x л/2 from the left, cos x is never large enough for x+cosx to be greater than л/2 and cot x is never small enough for x + cot x to be less than x/2.)arrow_forward1. Show that f(x) = x3 is not uniformly continuous on R. 2. Show that f(x) = 1/(x-2) is not uniformly continuous on (2,00). 3. Show that f(x)=sin(1/x) is not uniformly continuous on (0,л/2]. 4. Show that f(x) = mx + b is uniformly continuous on R. 5. Show that f(x) = 1/x2 is uniformly continuous on [1, 00), but not on (0, 1]. 6. Show that if f is uniformly continuous on [a, b] and uniformly continuous on D (where D is either [b, c] or [b, 00)), then f is uniformly continuous on [a, b]U D. 7. Show that f(x)=√x is uniformly continuous on [1, 00). Use Exercise 6 to conclude that f is uniformly continuous on [0, ∞). 8. Show that if D is bounded and f is uniformly continuous on D, then fis bounded on D. 9. Let f and g be uniformly continuous on D. Show that f+g is uniformly continuous on D. Show, by example, that fg need not be uniformly con- tinuous on D. 10. Complete the proof of Theorem 4.7. 11. Give an example of a continuous function on Q that cannot be continuously extended to R. 12.…arrow_forwardcan I see the steps for how you got the same answers already provided for μ1->μ4. this is a homework that provide you answers for question after attempting it three triesarrow_forward
- 1. Prove that for each n in N, 1+2++ n = n(n+1)/2. 2. Prove that for each n in N, 13 +23+ 3. Prove that for each n in N, 1+3+5+1 4. Prove that for each n ≥ 4,2" -1, then (1+x)" ≥1+nx for each n in N. 11. Prove DeMoivre's Theorem: fort a real number, (cost+i sint)" = cos nt + i sinnt for each n in N, where i = √√-1.arrow_forwardPls help ASAParrow_forward2. Sam and Deb have a weekly net income of $1500. They have a pet dog. Their monthly expenses, not related to housing, are $2875. They have savings of $32 000. They are considering two housing options: Option 1: Renting a 2-bedroom condo for $1650 a month, plus utilities averaging $210 a month Option 2: Buying a 2-bedroom condo for a down payment of $24 500, bi-weekly mortgage payments of $1100, and a monthly condo fee of $475 a) Determine the monthly cost of each housing option. Factoring in other expenses not related to housing, which one can Sam and Deb afford? b) Suppose their dog falls ill and they have to pay $85 every week to cover veterinarian and medical expenses. Calculate the additional monthly expenses. How much money would be available for savings if they choose housing option 2?arrow_forward
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill