Chapter 3, Problem 3.52E

a.

To determine

To explain: The area within 1 standard deviation of the mean.

To compare: The area within 1 standard deviation of the mean by using applet and 68-95-99.7 rule.

Answer to Problem 3.52E

The area within 1 standard deviation of the mean is 0.6826.

The area within 1 standard deviation of the mean by using applet and 68-95-99.7 rule is both approximately equal.

Explanation of Solution

Given info:

The mean and standard deviation of the normal distribution are 0 and 1.

68-95-99.7 Rule:

About 68% of the observations fall within $\sigma$ of the mean $\mu$

About 95% of the observations fall within $2\sigma$ of the mean $\mu$

About 99.7% of the observations fall within $3\sigma$ of the mean $\mu$

Calculation:

Find the area of 1 standard deviation on either side of the mean using the normal density curve applet.

Applet procedure:

Step-by-step Applet procedure to find the area of 1 standard deviation on either side of the mean is given as follows:

• In Statistical Applets, choose Normal Density Curve.
• In the normal density curve drag one flag and place at 1 standard deviation on either side of the mean.

Output obtained from Applet:

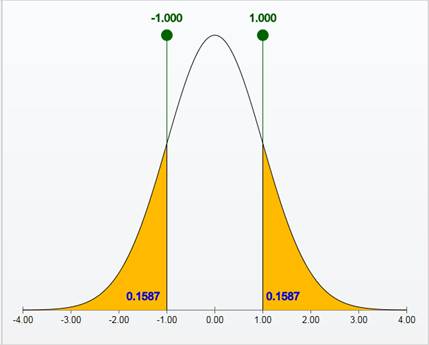
From the Applet output, the area of one standard deviation below −1 is 0.1587 and the above 1 is 0.1587.

The formula to find the area within 1 standard deviation of the mean is,

$\begin{array}{c}\left[\begin{array}{l}\text{Area within 1 standard deviations }\\ \text{of the mean}\end{array}\right]\text{ = }1-\left(\begin{array}{l}\text{Area to the left of }\left(-\text{1}\right)+\\ \text{Area to the right of 1}\end{array}\right)\\ =1-\left(0.1587+0.1587\right)\\ =1-0.3176\\ =0.6826\end{array}$

Thus, the area within 1 standard deviation of the mean is 0.6826. That is, about 68% of the observations fall within $\sigma$ of the mean $\mu$.

From the 68-95-99.7 rule, the area within 1 standard deviation of the mean is about 68%.

Justification:

The result of the area within 1 standard deviation of the mean is approximately same by using the applet and the 68-95-99.7 rule.

b.

To determine

To explain: The area within 2 standard deviations of the mean and the area within 3 standard deviations of the mean.

To compare: The area within 2 standard deviations of the mean and the area within 3 standard deviations of the mean by using applet and 68-95-99.7 rule.

Answer to Problem 3.52E

The area within 2 standard deviations of the mean is 0.9544 and the area within 3 standard deviations of the mean is 0.9974.

The area within 2 standard deviations of the mean by using applet and 68-95-99.7 rule is both approximately equal and the area within 3 standard deviations of the mean by using applet and 68-95-99.7 rule is both approximately equal.

Explanation of Solution

Calculation:

Finding the area of 2 standard deviations on either side of the mean:

Applet procedure:

Step-by-step Applet procedure to find the area of 2 standard deviations on either side of the mean is given as follows

• In Statistical Applets, choose Normal Density Curve.
• In the normal density curve drag one flag and place at 2 standard deviations on either side of the mean.

Output obtained from Applet:

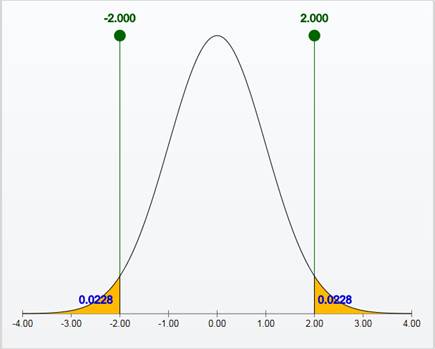
From the Applet output, the area to the left of −2 is 0.0228 and the area to right of 2 is 0.0228.

The formula to find the area within 2 standard deviations of the mean is,

$\begin{array}{c}\left[\begin{array}{l}\text{Area within 2 standard deviations }\\ \text{of the mean }\end{array}\right]\text{= }1-\left[\begin{array}{l}\text{Area to the left of }\left(-\text{2}\right)+\\ \text{Area to the right of 2}\end{array}\right]\\ =1-\left[0.0228+0.0228\right]\\ =1-0.0456\\ =0.9544\end{array}$

Thus, the area within 2 standard deviations of the mean is 0.9544. That is, about 95% of the observations fall within $2\sigma$ of the mean $\mu$.

From the 68-95-99.7 rule, the area within 2 standard deviations of the mean is about 95%.

Finding the area of 3 standard deviations on either side of the mean:

Applet Procedure:

Step-by-step Applet procedure to find the area of 3 standard deviations on either side of the mean is given as follows

• In Statistical Applets, choose Normal Density Curve.
• In the normal density curve drag one flag and place at 3 standard deviations on either side of the mean.

Output obtained from Applet:

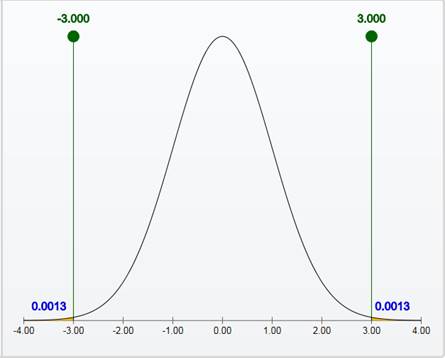
From the Applet output, the area to the left of −3 is 0.0013 and the area to right of 3 is 0.0013.

The formula to find the area within 3 standard deviations of the mean is,

$\begin{array}{c}\left[\begin{array}{l}\text{Area within 3 standard deviations }\\ \text{of the mean }\end{array}\right]\text{= }1-\left[\begin{array}{l}\text{Area to the left of }\left(-3\right)+\\ \text{Area to the right of 3}\end{array}\right]\\ =1-\left[0.0013+0.0013\right]\\ =1-0.0026\\ =0.9974\end{array}$

Thus, the area within 3 standard deviations of the mean is 0.9974. That is, about 99.7% of the observations fall within $3\sigma$ of the mean $\mu$.

From the 68-95-99.7 rule, the area within 3 standard deviations of the mean is about 99.7%.

Justification:

The result of the area within 2 standard deviations of the mean is approximately same by using the applet and the 68-95-99.7 rule and also the result of the area within 3 standard deviations of the mean is approximately same by using the applet and the 68-95-99.7 rule.