Single Variable Calculus: Early Transcendentals
Single Variable Calculus: Early Transcendentals
8th Edition
ISBN: 9781305270336
Author: James Stewart
Publisher: Cengage Learning
bartleby

Videos

Textbook Question
Book Icon
Chapter 3, Problem 22P

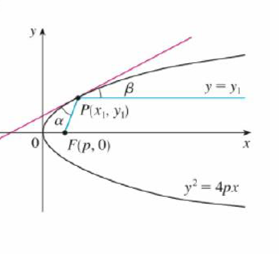
Let P(x1, y1) be a point on the parabola y2 = 4px with focus F(p, 0). Let α be the angle between the parabola and the line segment FP, and let β be the angle between the horizontal line y = y1, and the parabola as in the figure. Prove that α = β. (Thus. by a principle of geometrical optics. light from a source placed at F will be reflected along a line parallel to the x-axis. This explains why paraboloids, the surfaces obtained by rotating parabolas about their axes, are used as the shape of some automobile headlights and mirrors for telescopes.)

Chapter 3, Problem 22P, Let P(x1, y1) be a point on the parabola y2 = 4px with focus F(p, 0). Let be the angle between the

Expert Solution & Answer
Check Mark

Want to see the full answer?

Check out a sample textbook solution
Blurred answer
Previous
Chapter 3, Problem 21P
Next
Chapter 3, Problem 23P
Students have asked these similar questions
After a great deal of experimentation, two college senior physics majors determined that when a bottle of French champagne is shaken several times, held upright, and uncorked, its cork travels according to the function below, where s is its height (in feet) above the ground t seconds after being released. s(t)=-16t² + 30t+3 a. How high will it go? b. How long is it in the air?
+6x²+135x+1) (0≤x≤10). a) Find the number of units The total profit P(x) (in thousands of dollars) from a sale of x thousand units of a new product is given by P(x) = In (-x²+6x² + 135x+ that should be sold in order to maximize the total profit. b) What is the maximum profit?
The fox population in a certain region has an annual growth rate of 8 percent per year. It is estimated that the population in the year 2000 was 22600. (a) Find a function that models the population t years after 2000 (t = 0 for 2000). Your answer is P(t) = (b) Use the function from part (a) to estimate the fox population in the year 2008. Your answer is (the answer should be an integer)

Chapter 3 Solutions

Single Variable Calculus: Early Transcendentals

Ch. 3.1 - (a) How is the number e defined? (b) Use a...Ch. 3.1 - Prob. 2ECh. 3.1 - Differentiate the function. f(x) = 240Ch. 3.1 - Differentiate the function. f(x) = e5Ch. 3.1 - Differentiate the function. f(x) = 5.2x + 2.3Ch. 3.1 - Prob. 6ECh. 3.1 - Prob. 7ECh. 3.1 - Differentiate the function. f(t) = 1.4t5 2.5t2+...Ch. 3.1 - Prob. 9ECh. 3.1 - Prob. 10E
Ch. 3.1 - Prob. 11ECh. 3.1 - Differentiate the function. B(y) = cy6Ch. 3.1 - Prob. 13ECh. 3.1 - Differentiate the function. y = x5/3 x2/3Ch. 3.1 - Differentiate the function. R(a) = (3a + 1)2Ch. 3.1 - Differentiate the function. h(t)=t44etCh. 3.1 - Differentiate the function. S(p)=ppCh. 3.1 - Differentiate the function. y=x3(2+x)Ch. 3.1 - Differentiate the function. y=3ex+4x3Ch. 3.1 - Differentiate the function. S(R) = 4R2Ch. 3.1 - Prob. 21ECh. 3.1 - Prob. 22ECh. 3.1 - Prob. 23ECh. 3.1 - Prob. 24ECh. 3.1 - Prob. 25ECh. 3.1 - Prob. 26ECh. 3.1 - Prob. 27ECh. 3.1 - Prob. 28ECh. 3.1 - Prob. 29ECh. 3.1 - Differentiate the function. D(t)=1+16t2(4t)3Ch. 3.1 - Prob. 31ECh. 3.1 - Differentiate the function. y = ex + 1 + 1Ch. 3.1 - Prob. 33ECh. 3.1 - Find an equation of the tangent line to the curve...Ch. 3.1 - Find an equation of the tangent line to the curve...Ch. 3.1 - Prob. 36ECh. 3.1 - Find equations of the tangent line and normal line...Ch. 3.1 - Prob. 38ECh. 3.1 - Prob. 39ECh. 3.1 - Prob. 40ECh. 3.1 - Prob. 41ECh. 3.1 - Prob. 42ECh. 3.1 - Prob. 43ECh. 3.1 - Prob. 44ECh. 3.1 - Prob. 45ECh. 3.1 - Prob. 46ECh. 3.1 - Prob. 47ECh. 3.1 - Prob. 48ECh. 3.1 - Prob. 49ECh. 3.1 - Prob. 50ECh. 3.1 - Prob. 51ECh. 3.1 - Prob. 52ECh. 3.1 - Prob. 53ECh. 3.1 - Find the points on the curve y = 2x3 + 3x2 12x +...Ch. 3.1 - Prob. 56ECh. 3.1 - Prob. 57ECh. 3.1 - Prob. 58ECh. 3.1 - Prob. 59ECh. 3.1 - Prob. 60ECh. 3.1 - Prob. 61ECh. 3.1 - Where does the normal line to the parabola y = x2 ...Ch. 3.1 - Draw a diagram to show that there are two tangent...Ch. 3.1 - Prob. 64ECh. 3.1 - Prob. 65ECh. 3.1 - Find the nth derivative of each function by...Ch. 3.1 - Prob. 67ECh. 3.1 - The equation y" + y' 2y = x2 is called a...Ch. 3.1 - Find a cubic function y = ax3 + bx2 + cx + d whose...Ch. 3.1 - Prob. 70ECh. 3.1 - Prob. 71ECh. 3.1 - At what numbers is the following function g...Ch. 3.1 - Prob. 73ECh. 3.1 - Prob. 74ECh. 3.1 - Find the parabola with equation y = ax2 + bx whose...Ch. 3.1 - Prob. 76ECh. 3.1 - Prob. 77ECh. 3.1 - Prob. 78ECh. 3.1 - What is the value of c such that the line y = 2x +...Ch. 3.1 - Prob. 80ECh. 3.1 - Prob. 81ECh. 3.1 - A tangent line is drawn to the hyperbola xy = c at...Ch. 3.1 - Prob. 83ECh. 3.1 - Prob. 84ECh. 3.1 - Prob. 85ECh. 3.1 - Prob. 86ECh. 3.2 - Find the derivative of f(x) = (1 + 2x2)(x x2) in...Ch. 3.2 - Find the derivative o f the function...Ch. 3.2 - Prob. 3ECh. 3.2 - Differentiate. g(x)=(x+22)exCh. 3.2 - Differentiate. y=xexCh. 3.2 - Differentiate. y=ex1exCh. 3.2 - Prob. 7ECh. 3.2 - Differentiate. G(x)=x222x+1Ch. 3.2 - Differentiate. H(u)=(uu)(u+u)Ch. 3.2 - Prob. 10ECh. 3.2 - Prob. 11ECh. 3.2 - Prob. 12ECh. 3.2 - Prob. 13ECh. 3.2 - Prob. 14ECh. 3.2 - Prob. 15ECh. 3.2 - Prob. 16ECh. 3.2 - Prob. 17ECh. 3.2 - Prob. 18ECh. 3.2 - Prob. 19ECh. 3.2 - Prob. 20ECh. 3.2 - Prob. 21ECh. 3.2 - Prob. 22ECh. 3.2 - Prob. 23ECh. 3.2 - Differentiate. F(t)=AtBt2+Ct3Ch. 3.2 - Prob. 25ECh. 3.2 - Differentiate. f(x)=ax+bcx+dCh. 3.2 - Prob. 27ECh. 3.2 - Prob. 28ECh. 3.2 - Prob. 29ECh. 3.2 - Prob. 30ECh. 3.2 - Prob. 31ECh. 3.2 - Prob. 32ECh. 3.2 - Prob. 33ECh. 3.2 - Find equations of the tangent line and normal line...Ch. 3.2 - Prob. 35ECh. 3.2 - Prob. 36ECh. 3.2 - Prob. 37ECh. 3.2 - Prob. 38ECh. 3.2 - Prob. 39ECh. 3.2 - Prob. 40ECh. 3.2 - Prob. 41ECh. 3.2 - Prob. 42ECh. 3.2 - Prob. 43ECh. 3.2 - Prob. 44ECh. 3.2 - Prob. 45ECh. 3.2 - If h(2) = 4 and h'(2) = 3, find ddx(h(x)x)|x=2Ch. 3.2 - Prob. 47ECh. 3.2 - Prob. 48ECh. 3.2 - If f and g are the functions whose graphs are...Ch. 3.2 - Prob. 50ECh. 3.2 - Prob. 51ECh. 3.2 - If f is a differentiable function, find an...Ch. 3.2 - Prob. 53ECh. 3.2 - Find equations of the tangent lines to the curve...Ch. 3.2 - Prob. 55ECh. 3.2 - Prob. 56ECh. 3.2 - Prob. 57ECh. 3.2 - A manufacturer produces bolts of a fabric with a...Ch. 3.2 - Prob. 59ECh. 3.2 - The biomass B(t) of a fish population is the total...Ch. 3.2 - (a) Use the Product Rule twice to prove that if f,...Ch. 3.2 - (a) If F(x) = f(x) g(x), where f and g have...Ch. 3.2 - Find expressions for the first five derivatives of...Ch. 3.2 - Prob. 64ECh. 3.3 - Prob. 1ECh. 3.3 - Differentiate. f(x) = x cos x + 2 tan xCh. 3.3 - Differentiate. f(x) = ex cos xCh. 3.3 - Differentiate. y = 2 sec x csc xCh. 3.3 - Differentiate. y = sec tanCh. 3.3 - Prob. 6ECh. 3.3 - Prob. 7ECh. 3.3 - Prob. 8ECh. 3.3 - Prob. 9ECh. 3.3 - Prob. 10ECh. 3.3 - Differentiate f()=sin1+cosCh. 3.3 - Prob. 12ECh. 3.3 - Prob. 13ECh. 3.3 - Differentiate. y=sint1+tantCh. 3.3 - Differentiate. f() = cos sinCh. 3.3 - Differentiate. f(t) = tet cot tCh. 3.3 - Prob. 17ECh. 3.3 - Prob. 18ECh. 3.3 - Prob. 19ECh. 3.3 - Prove, using the definition of derivative. that if...Ch. 3.3 - Prob. 21ECh. 3.3 - Find an equation of the tangent line to the curve...Ch. 3.3 - Prob. 23ECh. 3.3 - Prob. 24ECh. 3.3 - Prob. 25ECh. 3.3 - Prob. 26ECh. 3.3 - Prob. 27ECh. 3.3 - Prob. 28ECh. 3.3 - If H() = sin , find H'() and H"( ).Ch. 3.3 - If f(t) = sec t, find f"(/4).Ch. 3.3 - Prob. 31ECh. 3.3 - Prob. 32ECh. 3.3 - For what values of x does the graph of f have a...Ch. 3.3 - Prob. 34ECh. 3.3 - Prob. 35ECh. 3.3 - An elastic band is hung on a hook and a mass is...Ch. 3.3 - Prob. 37ECh. 3.3 - Prob. 38ECh. 3.3 - Prob. 39ECh. 3.3 - Prob. 40ECh. 3.3 - Prob. 41ECh. 3.3 - Prob. 42ECh. 3.3 - Prob. 43ECh. 3.3 - Prob. 44ECh. 3.3 - Prob. 45ECh. 3.3 - Prob. 46ECh. 3.3 - Prob. 47ECh. 3.3 - Prob. 48ECh. 3.3 - Prob. 49ECh. 3.3 - Prob. 50ECh. 3.3 - Find the given derivative by finding the first few...Ch. 3.3 - Find the given derivative by finding the first few...Ch. 3.3 - Prob. 53ECh. 3.3 - Prob. 54ECh. 3.3 - Differentiate each trigonometric identity to...Ch. 3.3 - A semicircle with diameter PQ sits on an isosceles...Ch. 3.3 - The figure shows a circular arc of length s and a...Ch. 3.3 - Prob. 58ECh. 3.4 - Write the composite function in the form f(g(x))....Ch. 3.4 - Write the composite function in the form f(g(x))....Ch. 3.4 - Prob. 3ECh. 3.4 - Write the composite function in the form f(g(x))....Ch. 3.4 - Prob. 5ECh. 3.4 - Prob. 6ECh. 3.4 - Find the derivative of the function. F(x) = (5x6 +...Ch. 3.4 - Find the derivative of the function. F (x) = (1 +...Ch. 3.4 - Find the derivative of the function. f(x)=5x+1Ch. 3.4 - Prob. 10ECh. 3.4 - Prob. 11ECh. 3.4 - Prob. 12ECh. 3.4 - Prob. 13ECh. 3.4 - Find the derivative of the function. f(t) = t sin ...Ch. 3.4 - Prob. 15ECh. 3.4 - Prob. 16ECh. 3.4 - Find the derivative of the function. f(x) = (2x ...Ch. 3.4 - Find the derivative of the function. g(x) = (x2 +...Ch. 3.4 - Prob. 19ECh. 3.4 - Find the derivative of the function. F(t) = (3t ...Ch. 3.4 - Prob. 21ECh. 3.4 - Find the derivative of the function. y=(x+1x)5Ch. 3.4 - Prob. 23ECh. 3.4 - Find the derivative of the function. f(t)2t3Ch. 3.4 - Prob. 25ECh. 3.4 - Prob. 26ECh. 3.4 - Prob. 27ECh. 3.4 - Find the derivative of the function. f(z) =...Ch. 3.4 - Prob. 29ECh. 3.4 - Prob. 30ECh. 3.4 - Prob. 31ECh. 3.4 - Prob. 32ECh. 3.4 - Prob. 33ECh. 3.4 - Prob. 34ECh. 3.4 - Prob. 35ECh. 3.4 - Find the derivative of the function. y = x2 e1/xCh. 3.4 - Prob. 37ECh. 3.4 - Prob. 38ECh. 3.4 - Prob. 39ECh. 3.4 - Prob. 40ECh. 3.4 - Prob. 41ECh. 3.4 - Prob. 42ECh. 3.4 - Find the derivative of the function. g(x) = (2...Ch. 3.4 - Prob. 44ECh. 3.4 - Prob. 45ECh. 3.4 - Prob. 46ECh. 3.4 - Prob. 47ECh. 3.4 - Prob. 48ECh. 3.4 - Prob. 49ECh. 3.4 - Find y and y. y=eexCh. 3.4 - Find an equation of the tangent line to the curve...Ch. 3.4 - Find an equation of the tangent line to the curve...Ch. 3.4 - Prob. 53ECh. 3.4 - Prob. 54ECh. 3.4 - Prob. 55ECh. 3.4 - Prob. 56ECh. 3.4 - Prob. 57ECh. 3.4 - Prob. 58ECh. 3.4 - Prob. 59ECh. 3.4 - At what point on the curve y=1+2x is the tangent...Ch. 3.4 - Prob. 61ECh. 3.4 - Prob. 62ECh. 3.4 - A table of values for f, g, f, and g is given. (a)...Ch. 3.4 - Let f and g be the functions in Exercise 63. (a)...Ch. 3.4 - Prob. 65ECh. 3.4 - Prob. 66ECh. 3.4 - Prob. 67ECh. 3.4 - Suppose f is differentiable on and is a real...Ch. 3.4 - Suppose f is differentiable on . Let F(x) = f(ex)...Ch. 3.4 - Prob. 70ECh. 3.4 - Prob. 71ECh. 3.4 - Prob. 72ECh. 3.4 - Prob. 73ECh. 3.4 - Prob. 74ECh. 3.4 - Prob. 75ECh. 3.4 - Prob. 76ECh. 3.4 - Prob. 77ECh. 3.4 - Find the 1000th derivative of f(x) = xex.Ch. 3.4 - The displacement of a particle on a vibrating...Ch. 3.4 - If the equation of motion of a particle is given...Ch. 3.4 - Prob. 81ECh. 3.4 - Prob. 82ECh. 3.4 - The motion of a spring that is subject to a...Ch. 3.4 - Prob. 84ECh. 3.4 - The average blood alcohol concentration (BAC) of...Ch. 3.4 - In Section 1.4 we modeled the world population...Ch. 3.4 - Prob. 87ECh. 3.4 - Prob. 88ECh. 3.4 - Prob. 89ECh. 3.4 - The table gives the US population from 1790 to...Ch. 3.4 - Prob. 93ECh. 3.4 - Prob. 94ECh. 3.4 - (a) If n is a positive integer, prove that...Ch. 3.4 - Prob. 96ECh. 3.4 - Prob. 97ECh. 3.4 - Prob. 98ECh. 3.4 - Prob. 99ECh. 3.4 - If y = f(u) and u = g(x), where f and g possess...Ch. 3.5 - (a) Find y by implicit differentiation. (b) Solve...Ch. 3.5 - Prob. 2ECh. 3.5 - Prob. 3ECh. 3.5 - Prob. 4ECh. 3.5 - Find dy/dx by implicit differentiation. 5. x2 4xy...Ch. 3.5 - Prob. 6ECh. 3.5 - Find dy/dx by implicit differentiation. 7. x4 +...Ch. 3.5 - Find dy/dx by implicit differentiation. 8. x3 xy2...Ch. 3.5 - Find dy/dx by implicit differentiation. 9....Ch. 3.5 - Find dy/dx by implicit differentiation. 10. xey =...Ch. 3.5 - Find dy/dx by implicit differentiation. 11. y cos...Ch. 3.5 - Find dy/dx by implicit differentiation. 12....Ch. 3.5 - Find dy/dx by implicit differentiation. 13....Ch. 3.5 - Prob. 14ECh. 3.5 - Prob. 15ECh. 3.5 - Prob. 16ECh. 3.5 - Prob. 17ECh. 3.5 - Prob. 18ECh. 3.5 - Find dy/dx by implicit differentiation. 19....Ch. 3.5 - Prob. 20ECh. 3.5 - Prob. 21ECh. 3.5 - Prob. 22ECh. 3.5 - Regard y as the independent variable and x as the...Ch. 3.5 - Regard y as the independent variable and x as the...Ch. 3.5 - Prob. 25ECh. 3.5 - Use implicit differentiation to find an equation...Ch. 3.5 - Prob. 27ECh. 3.5 - Prob. 28ECh. 3.5 - Use implicit differentiation to find an equation...Ch. 3.5 - Prob. 30ECh. 3.5 - Use implicit differentiation to find an equation...Ch. 3.5 - Prob. 32ECh. 3.5 - (a) The curve with equation y2 = 5x4 x2 is called...Ch. 3.5 - Prob. 34ECh. 3.5 - Find y by implicit differentiation. 35. x2 + 4y2 =...Ch. 3.5 - Prob. 36ECh. 3.5 - Prob. 37ECh. 3.5 - Prob. 38ECh. 3.5 - Prob. 39ECh. 3.5 - If x2 + xy + y3 = 1, find the value of y at the...Ch. 3.5 - Prob. 43ECh. 3.5 - Prob. 44ECh. 3.5 - Find an equation of the tangent line to the...Ch. 3.5 - Prob. 46ECh. 3.5 - Show, using implicit differentiation, that any...Ch. 3.5 - Prob. 48ECh. 3.5 - Find the derivative of the function. Simplify...Ch. 3.5 - Find the derivative of the function. Simplify...Ch. 3.5 - Find the derivative of the function. Simplify...Ch. 3.5 - Prob. 52ECh. 3.5 - Prob. 53ECh. 3.5 - Find the derivative of the function. Simplify...Ch. 3.5 - Prob. 55ECh. 3.5 - Prob. 56ECh. 3.5 - Find the derivative of the function. Simplify...Ch. 3.5 - Prob. 58ECh. 3.5 - Prob. 59ECh. 3.5 - Prob. 60ECh. 3.5 - Prob. 61ECh. 3.5 - Prob. 62ECh. 3.5 - Prove the formula for (d/dx)(cos1x) by the same...Ch. 3.5 - (a) One way of defining sec1x is to say that...Ch. 3.5 - Prob. 65ECh. 3.5 - Prob. 66ECh. 3.5 - Prob. 67ECh. 3.5 - Two curves are orthogonal if their tangent lines...Ch. 3.5 - Show that the ellipse x2/a2 + y2/b2 = 1 and the...Ch. 3.5 - Prob. 70ECh. 3.5 - Prob. 71ECh. 3.5 - Prob. 73ECh. 3.5 - (a) Where does the normal line to the ellipse x2 ...Ch. 3.5 - Prob. 75ECh. 3.5 - Prob. 76ECh. 3.5 - Prob. 77ECh. 3.5 - Prob. 78ECh. 3.5 - The Bessel function of order 0, y = J(x),...Ch. 3.5 - The figure shows a lamp located three units to the...Ch. 3.6 - Explain why the natural logarithmic function y =...Ch. 3.6 - Differentiate the function. f(x) = x ln x xCh. 3.6 - Differentiate the function. f(x ) = sin(ln x)Ch. 3.6 - Differentiate the function. f(x) = ln(sin2x)Ch. 3.6 - Differentiate the function. f(x)=ln1xCh. 3.6 - Differentiate the function. y=1lnxCh. 3.6 - Prob. 7ECh. 3.6 - Prob. 8ECh. 3.6 - Prob. 9ECh. 3.6 - Prob. 10ECh. 3.6 - Differentiate the function. F(t) =(ln t)2 sin tCh. 3.6 - Differentiate the function. h(x)=ln(x+x21)Ch. 3.6 - Differentiate the function. G(y)=ln(2y+1)5y2+1Ch. 3.6 - Prob. 14ECh. 3.6 - Differentiate the function. F(s) = ln ln sCh. 3.6 - Differentiate the function. y = ln |1 + t t3|Ch. 3.6 - Differentiate the function. T(z) = 2z log2zCh. 3.6 - Prob. 18ECh. 3.6 - Prob. 19ECh. 3.6 - Differentiate the function. H(z)=a2z2a2+z2Ch. 3.6 - Prob. 21ECh. 3.6 - Prob. 22ECh. 3.6 - Prob. 23ECh. 3.6 - Find y and y. y=lnx1+lnxCh. 3.6 - Prob. 25ECh. 3.6 - Prob. 26ECh. 3.6 - Prob. 27ECh. 3.6 - Prob. 28ECh. 3.6 - Prob. 29ECh. 3.6 - Prob. 30ECh. 3.6 - Prob. 31ECh. 3.6 - Prob. 32ECh. 3.6 - Prob. 33ECh. 3.6 - Prob. 34ECh. 3.6 - Prob. 35ECh. 3.6 - Prob. 36ECh. 3.6 - Prob. 37ECh. 3.6 - Prob. 38ECh. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Prob. 40ECh. 3.6 - Prob. 41ECh. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Prob. 44ECh. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Prob. 46ECh. 3.6 - Prob. 47ECh. 3.6 - Prob. 48ECh. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Prob. 50ECh. 3.6 - Prob. 51ECh. 3.6 - Prob. 52ECh. 3.6 - Prob. 53ECh. 3.6 - Prob. 54ECh. 3.6 - Prob. 55ECh. 3.6 - Prob. 56ECh. 3.7 - A particle moves according to a law of motion s =...Ch. 3.7 - A particle moves according to a law of motion s =...Ch. 3.7 - A particle moves according to a law of motion s =...Ch. 3.7 - Prob. 4ECh. 3.7 - Prob. 5ECh. 3.7 - Prob. 6ECh. 3.7 - Prob. 7ECh. 3.7 - Prob. 8ECh. 3.7 - Prob. 9ECh. 3.7 - Prob. 10ECh. 3.7 - Prob. 11ECh. 3.7 - Prob. 12ECh. 3.7 - Prob. 13ECh. 3.7 - Prob. 14ECh. 3.7 - Prob. 15ECh. 3.7 - (a) The volume of a growing spherical cell is...Ch. 3.7 - Prob. 17ECh. 3.7 - Prob. 18ECh. 3.7 - The quantity of charge Q in coulombs (C) that has...Ch. 3.7 - Prob. 20ECh. 3.7 - Prob. 21ECh. 3.7 - Prob. 22ECh. 3.7 - Boyles Law states that when a sample of gas is...Ch. 3.7 - Prob. 24ECh. 3.7 - Prob. 25ECh. 3.7 - Prob. 26ECh. 3.7 - The table shows how the average age of first...Ch. 3.7 - Refer to the law of laminar flow given in Example...Ch. 3.7 - Prob. 30ECh. 3.7 - Prob. 31ECh. 3.7 - The cost function for a certain commodity is C(q)...Ch. 3.7 - Prob. 33ECh. 3.7 - Prob. 34ECh. 3.7 - Patients undergo dialysis treatment to remove urea...Ch. 3.7 - Invasive species often display a wave of advance...Ch. 3.7 - Prob. 37ECh. 3.7 - Prob. 38ECh. 3.7 - Prob. 39ECh. 3.8 - A population of protozoa develops with a constant...Ch. 3.8 - A common inhabitant of human intestines is the...Ch. 3.8 - A bacteria culture initially contains 100 cells...Ch. 3.8 - A bacteria culture grows with constant relative...Ch. 3.8 - The table gives estimates of the world population,...Ch. 3.8 - Prob. 6ECh. 3.8 - Prob. 7ECh. 3.8 - Strontium-90 has a half-life of 28 days. (a) A...Ch. 3.8 - Prob. 9ECh. 3.8 - Prob. 10ECh. 3.8 - Prob. 11ECh. 3.8 - Dinosaur fossils are too old to be reliably dated...Ch. 3.8 - Dinosaur fossils are often dated by using an...Ch. 3.8 - Prob. 14ECh. 3.8 - A roast turkey is taken from an oven when its...Ch. 3.8 - In a murder investigation, the temperature of the...Ch. 3.8 - Prob. 17ECh. 3.8 - Prob. 18ECh. 3.8 - Prob. 19ECh. 3.8 - (a) If 1000 is borrowed at 8% interest, find the...Ch. 3.8 - Prob. 21ECh. 3.8 - (a) How long will it take an investment to double...Ch. 3.9 - Prob. 1ECh. 3.9 - (a) If A is the area of a circle with radius r and...Ch. 3.9 - Prob. 3ECh. 3.9 - The length of a rectangle is increasing at a rate...Ch. 3.9 - A cylindrical tank with radius 5 m is being filled...Ch. 3.9 - Prob. 6ECh. 3.9 - The radius of a spherical ball is increasing at a...Ch. 3.9 - Prob. 8ECh. 3.9 - Suppose y=2x+1, where x and y are functions of t....Ch. 3.9 - Prob. 10ECh. 3.9 - If x2 + y2 + z2 = 9, dx/dt = 5, and dy/dt = 4,...Ch. 3.9 - A particle is moving along a hyperbola xy = 8. As...Ch. 3.9 - (a) What quantities are given in the problem? (b)...Ch. 3.9 - (a) What quantities are given in the problem? (b)...Ch. 3.9 - (a) What quantities are given in the problem? (b)...Ch. 3.9 - (a) What quantities are given in the problem? (b)...Ch. 3.9 - Two cars start moving from the same point. One...Ch. 3.9 - Prob. 18ECh. 3.9 - A man starts walking north at 4 ft/s from a point...Ch. 3.9 - A baseball diamond is a square with side 90 ft. A...Ch. 3.9 - Prob. 21ECh. 3.9 - A boat is pulled into a dock by a rope attached to...Ch. 3.9 - Prob. 23ECh. 3.9 - Prob. 24ECh. 3.9 - Water is leaking out of an inverted conical tank...Ch. 3.9 - A trough is 10 ft long and its ends have the shape...Ch. 3.9 - A water trough is 10m long and a cross-section has...Ch. 3.9 - Prob. 28ECh. 3.9 - Gravel is being dumped from a conveyor belt at a...Ch. 3.9 - A kite 100ft above the ground moves horizontally...Ch. 3.9 - The sides of an equilateral triangle are...Ch. 3.9 - How fast is the angle between the ladder and the...Ch. 3.9 - Prob. 33ECh. 3.9 - Prob. 34ECh. 3.9 - If the minute hand of a clock has length r (in...Ch. 3.9 - Prob. 36ECh. 3.9 - Boyles Law states that when a sample of gas is...Ch. 3.9 - When air expands adiabatically (without gaining or...Ch. 3.9 - Prob. 39ECh. 3.9 - Prob. 40ECh. 3.9 - Prob. 41ECh. 3.9 - Two carts, A and B, are connected by a rope 39 ft...Ch. 3.9 - Prob. 43ECh. 3.9 - A lighthouse is located on a small island 3 km...Ch. 3.9 - Prob. 45ECh. 3.9 - Prob. 46ECh. 3.9 - Prob. 47ECh. 3.9 - Prob. 48ECh. 3.9 - Prob. 49ECh. 3.9 - Prob. 50ECh. 3.10 - Find the linearization L(x) of the function at n....Ch. 3.10 - Find the linearization L(x) of the function at n....Ch. 3.10 - Find the linearization L(x) of the function at n....Ch. 3.10 - Find the linearization L(x) of the function at n....Ch. 3.10 - Find the linear approximation of the function...Ch. 3.10 - Prob. 6ECh. 3.10 - Prob. 7ECh. 3.10 - Prob. 8ECh. 3.10 - Verify the given linear approximation at a = 0....Ch. 3.10 - Verify the given linear approximation at a = 0....Ch. 3.10 - Find the differential of each function. 11. (a) y...Ch. 3.10 - Prob. 12ECh. 3.10 - Find the differential of each function. 13. (a)...Ch. 3.10 - Prob. 14ECh. 3.10 - (a) Find the differential dy and (b) evaluate dy...Ch. 3.10 - Prob. 16ECh. 3.10 - (a) Find the differential dy and (b) evaluate dy...Ch. 3.10 - (a) Find the differential dy and (b) evaluate dy...Ch. 3.10 - Compute y and dy for the given values of x and dx...Ch. 3.10 - Prob. 20ECh. 3.10 - Prob. 21ECh. 3.10 - Compute y and dy for the given values of x and dx...Ch. 3.10 - Use a linear approximation (or differentials) to...Ch. 3.10 - Prob. 24ECh. 3.10 - Use a linear approximation (or differentials) to...Ch. 3.10 - Use a linear approximation (or differentials) to...Ch. 3.10 - Prob. 27ECh. 3.10 - Prob. 28ECh. 3.10 - Prob. 29ECh. 3.10 - Explain, in terms of linear approximations or...Ch. 3.10 - Prob. 31ECh. 3.10 - Prob. 32ECh. 3.10 - Prob. 33ECh. 3.10 - Prob. 34ECh. 3.10 - The circumference of a sphere was measured to be...Ch. 3.10 - Use differentials to estimate the amount of paint...Ch. 3.10 - Prob. 37ECh. 3.10 - Prob. 38ECh. 3.10 - Prob. 39ECh. 3.10 - When blood flows along a blood vessel, the flux F...Ch. 3.10 - Prob. 41ECh. 3.10 - On page 431 of Physics: Calculus, 2d ed., by...Ch. 3.10 - Prob. 43ECh. 3.10 - Prob. 44ECh. 3.11 - Find the numerical value of each expression. 1....Ch. 3.11 - Find the numerical value of each expression. 2....Ch. 3.11 - Prob. 3ECh. 3.11 - Prob. 4ECh. 3.11 - Prob. 5ECh. 3.11 - Prob. 6ECh. 3.11 - Prob. 7ECh. 3.11 - Prob. 8ECh. 3.11 - Prob. 9ECh. 3.11 - Prob. 10ECh. 3.11 - Prob. 11ECh. 3.11 - Prob. 12ECh. 3.11 - Prob. 13ECh. 3.11 - Prob. 14ECh. 3.11 - Prove the identity. 15. sinh 2x = 2 sinh x cosh xCh. 3.11 - Prob. 16ECh. 3.11 - Prob. 17ECh. 3.11 - Prob. 18ECh. 3.11 - Prove the identity. 19. (cosh x + sinh x)n = cosh...Ch. 3.11 - Prob. 20ECh. 3.11 - Prob. 21ECh. 3.11 - Prob. 22ECh. 3.11 - Prob. 23ECh. 3.11 - Prob. 24ECh. 3.11 - Prob. 25ECh. 3.11 - Prob. 26ECh. 3.11 - Prob. 27ECh. 3.11 - Prob. 28ECh. 3.11 - Prob. 29ECh. 3.11 - Prob. 30ECh. 3.11 - Prob. 31ECh. 3.11 - Prob. 32ECh. 3.11 - Prob. 33ECh. 3.11 - Prob. 34ECh. 3.11 - Prob. 35ECh. 3.11 - Find the derivative. Simplify where possible. 36....Ch. 3.11 - Find the derivative. Simplify where possible. 37....Ch. 3.11 - Prob. 38ECh. 3.11 - Prob. 39ECh. 3.11 - Find the derivative. Simplify where possible. 40....Ch. 3.11 - Find the derivative. Simplify where possible. 41....Ch. 3.11 - Prob. 42ECh. 3.11 - Prob. 43ECh. 3.11 - Prob. 44ECh. 3.11 - Prob. 45ECh. 3.11 - Prob. 46ECh. 3.11 - Prob. 47ECh. 3.11 - Prob. 48ECh. 3.11 - Prob. 49ECh. 3.11 - Prob. 50ECh. 3.11 - Prob. 51ECh. 3.11 - Prob. 52ECh. 3.11 - A cable with linear density = 2 kg/m is strung...Ch. 3.11 - A model for the velocity of a falling object after...Ch. 3.11 - Prob. 55ECh. 3.11 - Prob. 56ECh. 3.11 - Prob. 57ECh. 3.11 - Prob. 58ECh. 3 - State each differentiation rule both in symbols...Ch. 3 - Prob. 2RCCCh. 3 - Prob. 3RCCCh. 3 - Prob. 4RCCCh. 3 - Give several examples of how the derivative can be...Ch. 3 - Prob. 6RCCCh. 3 - Prob. 7RCCCh. 3 - Prob. 1RQCh. 3 - Prob. 2RQCh. 3 - Prob. 3RQCh. 3 - Prob. 4RQCh. 3 - Prob. 5RQCh. 3 - Prob. 6RQCh. 3 - Determine whether the statement is true or false....Ch. 3 - Prob. 8RQCh. 3 - Prob. 9RQCh. 3 - Prob. 10RQCh. 3 - Prob. 11RQCh. 3 - Prob. 12RQCh. 3 - Prob. 13RQCh. 3 - Prob. 14RQCh. 3 - Determine whether the statement is true or false....Ch. 3 - Prob. 1RECh. 3 - Prob. 2RECh. 3 - Prob. 3RECh. 3 - Prob. 4RECh. 3 - Prob. 5RECh. 3 - Prob. 6RECh. 3 - Prob. 7RECh. 3 - Prob. 8RECh. 3 - Prob. 9RECh. 3 - Prob. 10RECh. 3 - Prob. 11RECh. 3 - Calculate y'. 12. y = (arcsin 2x)2Ch. 3 - Prob. 13RECh. 3 - Prob. 14RECh. 3 - Prob. 15RECh. 3 - Prob. 16RECh. 3 - Calculate y'. 17. y=arctanCh. 3 - Prob. 18RECh. 3 - Prob. 19RECh. 3 - Prob. 20RECh. 3 - Prob. 21RECh. 3 - Prob. 22RECh. 3 - Prob. 23RECh. 3 - Prob. 24RECh. 3 - Prob. 25RECh. 3 - Prob. 26RECh. 3 - Prob. 27RECh. 3 - Prob. 28RECh. 3 - Prob. 29RECh. 3 - Calculate y'. 30. y=(x2+1)4(2x+1)3(3x1)5Ch. 3 - Prob. 31RECh. 3 - Prob. 32RECh. 3 - Prob. 33RECh. 3 - Prob. 34RECh. 3 - Prob. 35RECh. 3 - Prob. 36RECh. 3 - Prob. 37RECh. 3 - Prob. 38RECh. 3 - Prob. 39RECh. 3 - Prob. 40RECh. 3 - Prob. 41RECh. 3 - Prob. 42RECh. 3 - Prob. 43RECh. 3 - Prob. 44RECh. 3 - Prob. 45RECh. 3 - Prob. 46RECh. 3 - Prob. 47RECh. 3 - Prob. 48RECh. 3 - Prob. 49RECh. 3 - Prob. 50RECh. 3 - Prob. 51RECh. 3 - Prob. 52RECh. 3 - Prob. 53RECh. 3 - Prob. 54RECh. 3 - Prob. 55RECh. 3 - Prob. 56RECh. 3 - Prob. 57RECh. 3 - Prob. 58RECh. 3 - Prob. 59RECh. 3 - Prob. 60RECh. 3 - Prob. 61RECh. 3 - Prob. 62RECh. 3 - Prob. 63RECh. 3 - Prob. 64RECh. 3 - Prob. 65RECh. 3 - Prob. 66RECh. 3 - Prob. 67RECh. 3 - Prob. 68RECh. 3 - Prob. 69RECh. 3 - Prob. 70RECh. 3 - Prob. 71RECh. 3 - Prob. 72RECh. 3 - Prob. 73RECh. 3 - Prob. 74RECh. 3 - Prob. 75RECh. 3 - Prob. 76RECh. 3 - Prob. 77RECh. 3 - Prob. 78RECh. 3 - Prob. 79RECh. 3 - Prob. 80RECh. 3 - Prob. 81RECh. 3 - Prob. 82RECh. 3 - Prob. 83RECh. 3 - Prob. 84RECh. 3 - Prob. 85RECh. 3 - Prob. 86RECh. 3 - Prob. 87RECh. 3 - A particle moves along a horizontal line so that...Ch. 3 - A particle moves on a vertical line so that its...Ch. 3 - Prob. 90RECh. 3 - Prob. 91RECh. 3 - Prob. 92RECh. 3 - Prob. 93RECh. 3 - Prob. 94RECh. 3 - Prob. 95RECh. 3 - Prob. 96RECh. 3 - Prob. 97RECh. 3 - Prob. 98RECh. 3 - A balloon is rising at a constant speed of 5 ft/s....Ch. 3 - Prob. 100RECh. 3 - Prob. 101RECh. 3 - Prob. 102RECh. 3 - Prob. 103RECh. 3 - Prob. 104RECh. 3 - Prob. 105RECh. 3 - Prob. 106RECh. 3 - Prob. 107RECh. 3 - Prob. 108RECh. 3 - Prob. 109RECh. 3 - Suppose f is a differentiable function such that...Ch. 3 - Prob. 111RECh. 3 - Prob. 112RECh. 3 - Prob. 1PCh. 3 - Prob. 2PCh. 3 - Prob. 3PCh. 3 - Prob. 4PCh. 3 - Prob. 5PCh. 3 - Prob. 6PCh. 3 - Prob. 7PCh. 3 - Prob. 8PCh. 3 - Prob. 9PCh. 3 - Prob. 10PCh. 3 - Prob. 11PCh. 3 - Prob. 12PCh. 3 - Prob. 13PCh. 3 - If f(x)=x46+x45+21+x, calculate f(46)(3). Express...Ch. 3 - The figure shows a rotating wheel with radius 40...Ch. 3 - Prob. 16PCh. 3 - Prob. 17PCh. 3 - Prob. 18PCh. 3 - Let T and N be the tangent and normal lines to the...Ch. 3 - Prob. 20PCh. 3 - Prob. 21PCh. 3 - Let P(x1, y1) be a point on the parabola y2 = 4px...Ch. 3 - Prob. 23PCh. 3 - Prob. 24PCh. 3 - Prob. 25PCh. 3 - Prob. 27PCh. 3 - Prob. 28PCh. 3 - Prob. 29PCh. 3 - Prob. 30PCh. 3 - Find the two points on the curve y = x4 2x2 x...Ch. 3 - Prob. 32PCh. 3 - Prob. 33PCh. 3 - Prob. 34PCh. 3 - Prob. 35P

Additional Math Textbook Solutions

Find more solutions based on key concepts
1. How much money is Joe earning when he’s 30?

Pathways To Math Literacy (looseleaf)

Is there a relationship between wine consumption and deaths from heart disease? The table gives data from 19 de...

College Algebra Essentials (5th Edition)

23. A plant nursery sells two sizes of oak trees to landscapers. Large trees cost the nursery $120 from the gro...

College Algebra (Collegiate Math)

True or False The quotient of two polynomial expressions is a rational expression, (p. A35)

Precalculus

CHECK POINT I Consider the six jokes about books by Groucho Marx. Bob Blitzer. Steven Wright, HennyYoungman. Je...

Thinking Mathematically (6th Edition)

Students in a Listening Responses class bought 40 tickets for a piano concert. The number of tickets purchased ...

Elementary and Intermediate Algebra: Concepts and Applications (7th Edition)

Knowledge Booster
Background pattern image
Calculus
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Text book image
Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Text book image
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Text book image
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
SEE MORE TEXTBOOKS
Implicit Differentiation Explained - Product Rule, Quotient & Chain Rule - Calculus; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=LGY-DjFsALc;License: Standard YouTube License, CC-BY