
The paper “Lessons from Pacemaker Implantations” (Journal of the American Medical Association [1965]: 231–232) gave the results of a study that followed 89 heart patients who had received electronic pacemakers. The time (in months) to the first electrical malfunction of the pacemaker was recorded:
![Chapter 3, Problem 12CRE, The paper Lessons from Pacemaker Implantations (Journal of the American Medical Association [1965]:](https://content.bartleby.com/tbms-images/9781337793612/Chapter-3/images/93612-3-12cre-question-digital_image_001.png)
- a. Summarize these data in the form of a frequency distribution, using class intervals of 0 to <6, 6 to <12, and so on.
- b. Calculate the relative frequencies and cumulative relative frequencies for each class interval of the frequency distribution of Part (a).
- c. Show how the relative frequency for the class interval 12 to <18 could be obtained from the cumulative relative frequencies.
- d. Use the cumulative relative frequencies to give approximate answers to the following:
- i. What proportion of those who participated in the study had pacemakers that did not malfunction within the first year?
- ii. If the pacemaker must be replaced as soon as the first electrical malfunction occurs, approximately what proportion required replacement between 1 and 2 years after implantation?
- e. Construct a cumulative relative frequency plot, and use it to answer the following questions.
- i. What is the approximate time at which 50% of the pacemakers had failed?
- ii. What is the approximate time at which only 10% of the pacemakers initially implanted were still
functioning ?
a.
Construct the frequency distribution for the given data.
Answer to Problem 12CRE
The frequency distribution is given below.
| Class interval | Frequency |
| 0-<6 | 2 |
| 6-<12 | 10 |
| 12-<18 | 21 |
| 18-<24 | 28 |
| 24-<30 | 22 |
| 30-<36 | 6 |
Explanation of Solution
Calculation:
The data represents the time to the first electrical malfunction of the pacemaker for 89 heart patients.
Software procedure:
Frequency distribution:
The number of values lying in the particular interval or the number of times each value repeats is the frequency of that particular class interval or event.
The frequencies are calculated by using the tally mark. Here, the number of times each activity repeats is the frequency of that particular physical activity.
Here, the number of values time under the specified interval is the frequency of that particular class interval of time.
Here, the number of values in between the class interval 0-<6 is 2.
Therefore, the frequency of the class interval 0-<6 is 2.
Similarly, the frequencies of all the remaining class intervals are as follows:
| Class interval | Tally | Frequency |
| 0-<6 | 2 | |
| 6-<12 | 10 | |
| 12-<18 | 21 | |
| 18-<24 | 28 | |
| 24-<30 | 22 | |
| 30-<36 | 6 | |
| Total | 89 |
b.
Construct the relative frequency distribution for the given data.
Construct the cumulative relative frequency distribution for the given data.
Answer to Problem 12CRE
The relative frequency distribution and cumulative relative frequency distribution are given below.
| Class interval | Relative frequency | Cumulative relative frequency |
| 0-<6 | 0.02247 | 0.02247 |
| 6-<12 | 0.11236 | 0.13483 |
| 12-<18 | 0.23596 | 0.37079 |
| 18-<24 | 0.31461 | 0.6854 |
| 24-<30 | 0.24719 | 0.39259 |
| 30-<36 | 0.06742 | 1 |
Explanation of Solution
Calculation:
The general formula to obtain the relative frequency is given below:
Substitute the frequency of the class interval 0-<6 as “2” and the total frequency as “89” in relative frequency.
Similarly, relative frequencies for the remaining class intervals are obtained below:
| Class interval | Frequency | Relative frequency |
| 0-<6 | 2 | |
| 6-<12 | 10 | |
| 12-<18 | 21 | |
| 18-<24 | 28 | |
| 24-<30 | 22 | |
| 30-<36 | 6 |
Cumulative relative frequency:
Cumulative relative frequency is the sum of relative frequencies of all the previous events which are arranged in an order from smallest to largest value.
The general formula to obtain cumulative frequency using frequency distribution is,
From the relative frequencies, the cumulative relative frequencies are obtained as follows:
| Class interval | Relative frequency | Cumulative relative frequency |
| 0-<6 | 0.02247 | |
| 6-<12 | 0.11236 | |
| 12-<18 | 0.23596 | |
| 18-<24 | 0.31461 | |
| 24-<30 | 0.24719 | |
| 30-<36 | 0.06742 |
c.
Obtain the relative frequency for the class interval 12-18 using the cumulative frequency distribution.
Answer to Problem 12CRE
The relative frequency for the class interval 12-18 using the cumulative frequency distribution is 0.23596.
Explanation of Solution
Calculation:
The general formula to obtain cumulative frequency using frequency distribution is given below:
Relative frequency of a present event is obtained using the formula given below:
From the cumulative relative frequency distribution, relative frequency distribution is obtained as given below:
Thus, the relative frequency for the class interval 12-18 using the cumulative frequency distribution is 0.23596.
d.
(i). Find the approximate proportion of heart patients who had pacemakers that did not malfunction within the first year.
(ii) Find the approximate proportion of heart patients who required replacement between 1 and 2 years after implantation.
Answer to Problem 12CRE
(i) The approximate proportion of heart patients who had pacemakers that did not malfunction within the first year is 0.86517.
(ii) The approximate proportion of heart patients who required replacement between 1 and 2 years after implantation is 0.55057.
Explanation of Solution
Calculation:
The general formula for the relative frequency or proportion is,
(i). Approximate proportion of heart patients who had pacemakers that did not malfunction within the first year:
The Objective is to find the cumulative relative frequency of heart patients who had pacemakers that did not malfunction within the first year.
The cumulative relative frequency of heart patients who had pacemakers that malfunction within the first year is 0.13483.
That is, the proportion of heart patients who had pacemakers that malfunction within the first year is 0.13483.
Hence, the cumulative relative frequency of heart patients who had pacemakers that did not malfunction within the first year is obtained as given below:
Thus, the approximate proportion of heart patients who had pacemakers that did not malfunction within the first year is 0.86517.
(ii). Approximate proportion of heart patients who required replacement between 1 and 2 years after implantation:
The Objective is to find the relative frequency of heart patients required replacement between 1 and 2 years after implantation.
The relative frequency of heart patients required replacement between 1 and 2 years after implantation is obtained as given below:
Thus, the approximate proportion of heart patients who required replacement between 1 and 2 years after implantation is 0.55057.
e.
Plot the cumulative frequency distribution for the given data.
(i) Find the approximate time at which 50% of the pacemakers had failed.
(ii) Find the approximate time at which only 10% of the initially implanted pacemakers are functioning.
Answer to Problem 12CRE
Cumulative distribution plot is given below:
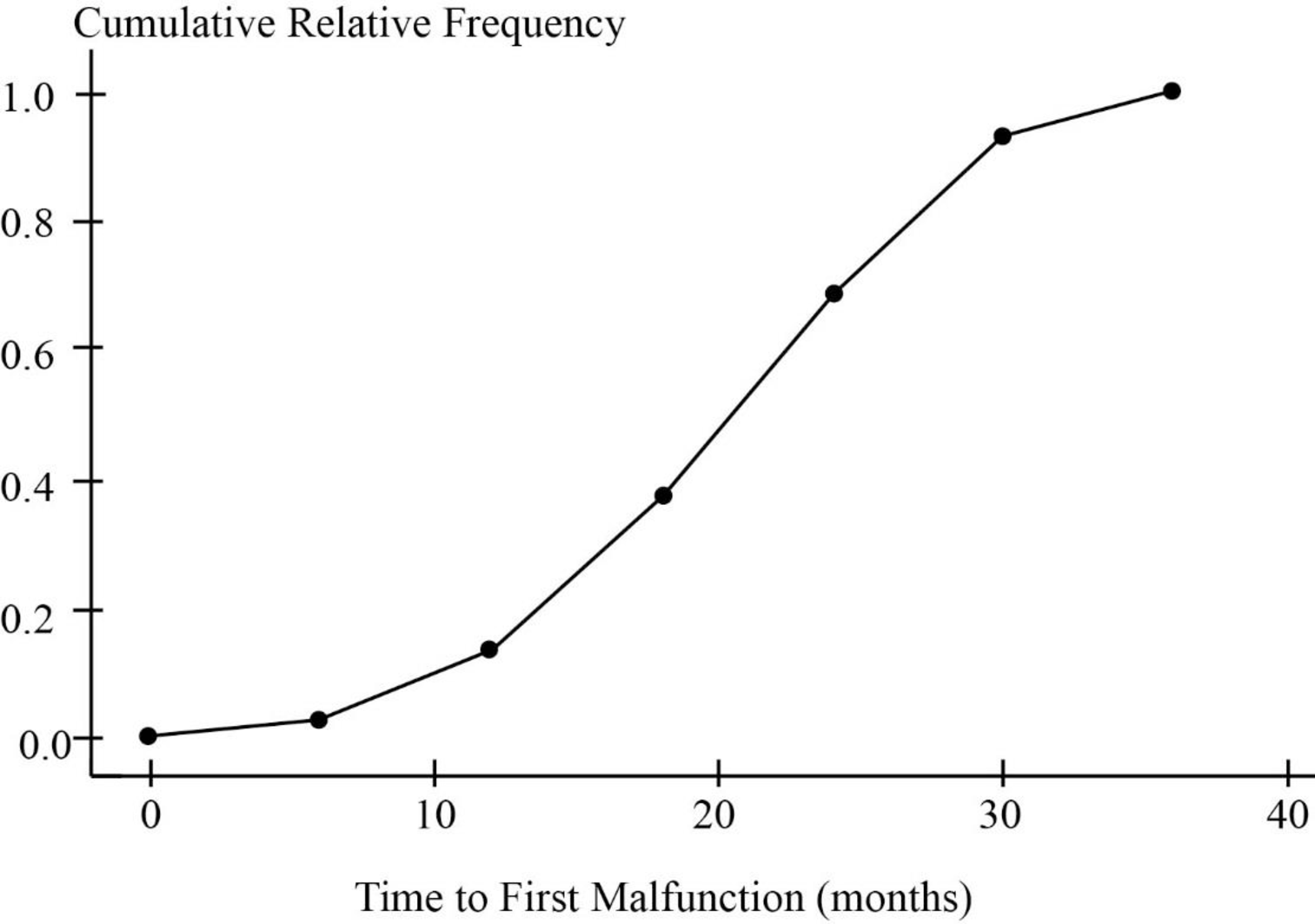
(i) The time at which 50% of the pacemakers had failed will be in between 18-<24 months.
(ii) The approximate time at which only 10% of the initially implanted pacemakers are functioning will be in between 24-<30 months.
Explanation of Solution
Calculation:
The cumulative relative frequency histogram is plotted for the given data.
Procedure to plot cumulative distribution plot:
Step by step procedure to draw the cumulative distribution plot is given below.
- Draw a horizontal axis and a vertical axis.
- The horizontal axis represents the cumulative frequencies.
- The vertical axis represents the “Time to first malfunction in months”.
- Plot each of the 6 cumulative frequencies corresponding to the time to first malfunction in months.
- Connect all the 6 plotted points of cumulative frequencies with a line.
The general formula for the relative frequency or proportion is,
(i). Approximate time at which 50% of the pacemakers had failed:
The Objective is to find the time at which 50% of the pacemakers had failed.
From the cumulative relative frequency distribution, 0.6854 corresponds to the interval 18-<24 months.
The cumulative relative frequency of 0.5 is less than the cumulative relative frequency of 0.6854.
Thus, the time at which 50% of the pacemakers had failed will be in between 18-<24 months.
(ii). Approximate time at which only 10% of the initially implanted pacemakers are functioning:
The Objective is to find the time only 10% of the initially implanted pacemakers are functioning.
In other words it can be said that, the time at which 90% of the pacemakers had failed.
From the cumulative relative frequency distribution, 0.93259 corresponds to the interval 24-<30 months.
The cumulative relative frequency of 0.9 is less than the cumulative relative frequency of 0.93259.
Thus, the time at which only 10% of the initially implanted pacemakers are functioning will be in between 24-<30 months.
Want to see more full solutions like this?
Chapter 3 Solutions
Introduction To Statistics And Data Analysis
Additional Math Textbook Solutions
Pathways To Math Literacy (looseleaf)
College Algebra (Collegiate Math)
Elementary and Intermediate Algebra: Concepts and Applications (7th Edition)
Precalculus
Elementary Statistics ( 3rd International Edition ) Isbn:9781260092561
APPLIED STAT.IN BUS.+ECONOMICS
- Urban Travel Times Population of cities and driving times are related, as shown in the accompanying table, which shows the 1960 population N, in thousands, for several cities, together with the average time T, in minutes, sent by residents driving to work. City Population N Driving time T Los Angeles 6489 16.8 Pittsburgh 1804 12.6 Washington 1808 14.3 Hutchinson 38 6.1 Nashville 347 10.8 Tallahassee 48 7.3 An analysis of these data, along with data from 17 other cities in the United States and Canada, led to a power model of average driving time as a function of population. a Construct a power model of driving time in minutes as a function of population measured in thousands b Is average driving time in Pittsburgh more or less than would be expected from its population? c If you wish to move to a smaller city to reduce your average driving time to work by 25, how much smaller should the city be?arrow_forwardHealth care workers who use latex gloves with glove powder on a daily basis are particularly susceptible to developing a latex allergy. Each in a sample of 44 hospital employees who were diagnosed with a latex allergy based on a skin-prick test reported on their exposure to latex gloves. Summary statistics for the number of latex gloves used per week are x= 19.4 and s = 11.7. Complete parts (a) - (d). a. Give a point estimate for the average number of latex gloves used per week by all health care workers with a latex allergy. b. Form a 95% confidence interval for the average number of latex gloves used per week by all health care workers with a latex allergy. (Use integers or decimals for any numbers in the expression. Round to two decimal places as needed.) c. Give a practical interpretation of the interval, part (b). O A. One can be 95% confident that latex gloves cause allergies for all who use a number of gloves contained in the interval. O B. One can be 95% confident that the…arrow_forwardParticipants (N=12) in a study were randomly assigned to one of two types of therapy – either talk therapy or drug therapy (n = 6 per condition). Mood scores were analyzed at two time points for all clients: 4 weeks and 12 weeks into the start of the therapy. Mood scores are presented in the table below, with higher scores indicating improved / more positive moods. Use the data to answer the questions in this set.arrow_forward
- Here is the question: An experiment has developed an "excitability score" for rats as a composite of a number of behavior indices. The experimenter is looking for evidence of association between the excitability score and the strain the rat belongs to. Some 25 rats are selected at random from each of the four pure strains, giving a total of 100 individuals in all. Within each strain used in the experiment, a grouped frequency distribution of "excitability scores" is found, the same class intervals being used for each distribution. Test the hypothesis that all four strains have the same distribution, on the basis of the data (image).I'm having trouble understanding how to solve this problem, especially since there is no Expected table (or observed table). I tried calculating one but got incorrect values. What should I do? I wasn't sure if i was supposed to make chi square tests between strain 1 and strain 2, then strain 2 and strain 3, etc. I'd appreciate any advice, thanks!arrow_forwardPlease help me answer questions from pictures with the following information below: A random sample of n1 = 16 communities in western Kansas gave the following information for people under 25 years of age. x1: Rate of hay fever per 1000 population for people under 25 99 91 119 130 93 123 112 93 125 95 125 117 97 122 127 88 A random sample of n2 = 14 regions in western Kansas gave the following information for people over 50 years old. x2: Rate of hay fever per 1000 population for people over 50 94 109 99 95 110 88 110 79 115 100 89 114 85 96arrow_forwardA botanist opened a sample of 50 bean pods and counted the number of beans in each pod. The results obtained were as follows: 3 0 4 2 3 1 2 3 1 0 5 0 3 6 0 3 5 4 5 3 5 5 1 1 0 0 0 5 0 1 5 3 6 4 5 6 1 5 3 6 1 0 6 2 1 1 1 1 4 6 the frequency table for these data. Number of Beans in Pod Number of Bean Pods 0 9 1 11 2 3 3 8 4 4 5 9 6 6 Determine the range of variation:(X¯-S,X¯+S) = ( , )Round your answers to 2 decimal places as needed. Calculate what percent of the data values are within one standard deviation of the mean.Hint: Create a histogram on paper and shade the included region(s) on your histogram to help visualize the shaded area and help with calculations.Total area of shaded region = Round your answer to 2 decimal places as needed.Percent of area within one standard deviation =Round your answer to 2 decimal places as needed.arrow_forward
- Search and Rescue of DND provides various statistics on boating accidents in he Maritimes and B.C. These statistics include information on the wind speed at the time of the accident. The following chart includes information recorded for 184 accidents on both coasts for the same time period: Wind Conditions Accidents West Coast Accidents East Coast Nil 13 6 Light 74 42 Moderate 30 15 Strong or higher 3 1 a) Suppose xe indicates the wind conditions in the East Coast where xe=0 indicates Nil, xe=1 indicates Light, xe = 2 indicates moderate and xe = 3 indicates Strong or Storm. Also suppose that xw indicates the wind conditions on the West Coast and xt indicates…arrow_forwardA researcher asked a group of 11 children to report on a 7-point Likert scale how sociable they feel first thing in the morning (low scores indicate not very sociable, high score indicate very sociable). The data in the frequency table below were obtained. The means is: Score 7 1 1 4 2 3 2 2. 1. N = 11 O 1.00 O 1.57 O 4.00 O 2.00 6.arrow_forwardA researcher is interested in the relationship between birth order and personality (outgoing versus reserved). A sample of n = 100 people is obtained, all of whom grew up in families as one of three children. Each person is given a personality test, and the researcher also records the person’s birth-order position (1st born, 2nd, or 3rd). The frequencies from this study are shown in the following table. On the basis of these data, can the researcher conclude that there is a significant relation between birth order and personality? Test at the .05 level of significance. 1st 2nd 3rd Outgoing 13 31 16 Reserved 17 19 4arrow_forward
- The owner of an automobile repair shop studied the waiting times for customers who arrive at the shop for an oil change. The following data with waiting times in minutes were collected over a one-month period. 911 312 11 433 424 13 22 5 18 6 9 12 23 15 2 (a) Develop a frequency distribution using classes of 0-4, 5-9, 10-14, 15-19, and 20-24. Class Frequency 0-4 5-9 10-14 15-19 20-24 Total (b) Develop a relative frequency distribution using the classes in part (a). If required, round your answers to two decimal places. Class Relative Frequency 0-45-9 10-14 15-19 20-24 Total (c) Develop a cumulative frequency distribution using the classes in part (a). Class Cumulative Frequency 0-45-910-14 15-19 20-24 (d) Develop a cumulative relative frequency distribution using the classes in part (a). If required, round your answers to two decimal places. Class Cumulative Relative Frequency 0-4 5-9 10-14 15-19 20-24 (e) What proportion of customers need an oil change who wait 9 minutes or less? %arrow_forwardThomas wants to compare the mean concentration of carbon monoxide (CO) on residential versus commercial streets, since these differ in terms of car traffic. In each of three neighborhoods of Montréal (named A, B, and C below), he randomly chooses four locations for each type of street, for a total of 24 observations (2 street types x 3 neighborhoods x 4 locations). At each location, he measures CO concentration in the air over a period of 10 hours (8:00 AM-6:00 PM), and obtains the following data (in ppm/h). 10-a) Draw a graph that gives insight into the possible presence of an interaction between the two classification factors. Do you suspect the presence of an interaction? Explain why. IMG 4569 10-b)Test whether or not the difference between residential and commercial streets in mean atmospheric CO concentration is the same among the three neighborhoods, and whether or not CO concentration in the air is the same, on average, for the two types of streets. Note that Neighborhood is…arrow_forwardThomas wants to compare the mean concentration of carbon monoxide (CO) on residential versus commercial streets, since these differ in terms of car traffic. In each of three neighborhoods of Montréal (named A, B, and C below), he randomly chooses four locations for each type of street, for a total of 24 observations (2 street types x 3 neighborhoods x 4 locations). At each location, he measures CO concentration in the air over a period of 10 hours (8:00 AM-6:00 PM), and obtains the following data (in ppm/h). Question: Test whether or not the difference between residential and commercial streets in mean atmospheric CO concentration is the same among the three neighborhoods, and whether or not CO concentration in the air is the same, on average, for the two types of streets. Note that Neighborhood is considered a random block factor in the ANOVA. Use significant level= 0.05.arrow_forward
 Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill


