
Concept explainers
For the rectangular plate of Probs. 2.109 and 2.110, determine the tension in each of the three cables knowing that the weight of the plate is 792 N.
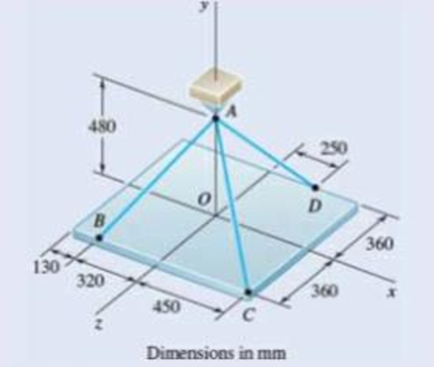
Fig. P2.109 and P2.110
The tension in three cables shown in figure
Answer to Problem 2.115P
The tension in cable
Explanation of Solution
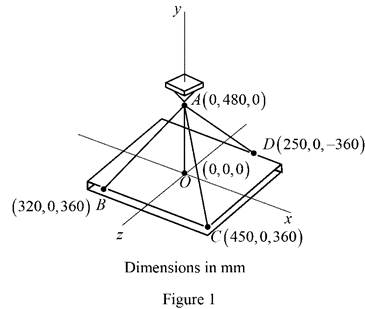
The sketch of plate supported by three cables is shown in figure 1.
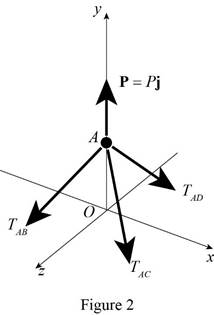
Free body diagram at
Here,
The weight of the plate is
Let
Let
Write the equation of vector distance
Here,
Write the vector distance of the cable
Here,
Write the vector distance of the cable
Here,
Write the equation of tension in the cable
Here,
Write the equation of
Write the equation of tension in the cable
Here,
Write the equation of
Write the equation of tension in the cable
Here,
Write the equation of
Write the equation of force exerting at point
Here,
Write the equilibrium condition for the forces at
Here, F is the force
The above equation implies that at equilibrium, total force acting on the cable at
Refer figure 2 and write the equation of equilibrium of forces at A.
Conclusion:
Substitute
Calculate the magnitude of
Substitute
Calculate the magnitude of
Substitute
Calculate the magnitude of
Substitute
Substitute
Substitute
(VII) to get
Substitute
Substitute
Substitute
Substitute
Since total force is zero. Equate force along each direction as zero.
Multiply equation (XII) with 12 and equation (XIV) with
Multiply equation (XII) with
Multiply equation (XV) with
Substitute
Substitute
Therefore, the tension in cable
Want to see more full solutions like this?
Chapter 2 Solutions
Vector Mechanics for Engineers: Statics and Dynamics
- I want to solve these choicesarrow_forward2. A spur gear made of bronze drives a mid steel pinion with angular velocity ratio of 32: 1. The pressure angle is 14½. It transmits 5 kW at 1800 r.p.m. of pinion. Considering only strength, design the smallest diameter gears and find also necessary face width. The number of teeth should not be less than 15 teeth on either gear. The elastic strength of bronze may be taken as 84 MPa and of steel as 105 MPa. Lewis factor for 14½½ pressure angle may be taken 0.684 0.124 y = No. of teeth as [Ans. m 3 mm; b= 35 mm; Dp = 48 mm; D= 168 mm]arrow_forwardQ2. Determine the safety factors for the bracket rod shown in Figure 2 based on both the distortion-energy theory and the maximum shear theory and compare them. Given: The material is 2024-T4 aluminum with a yield strength of 47 000 psi. The rod length /= 6 in. and arm a = 8 in. The rod outside diameter od 1.5 in., id = 1 in, h=2 in., t=0.5 in., Load F= 1000 lb. Assumptions: The load is static and the assembly is at room temperature. Consider shear due to transverse loading as well as other stresses. (Note: solve in SI units) wall tube Figure 2 armarrow_forward
- The question has been set up with all the cuts needed to accurately derive expressions for V(x) and M(x). Using the cuts free body diagrams set up below, derive expressions for V(x) and M(x). If you use the method of cuts then validate your answers using calculus or vice versa.arrow_forwardIt is required to treat 130 kmol/hr of chloroform-air feed gas mixture that contains 12% chloroform. It is required to remove 93% of chloroform using 150 kmol/hr of solvent that contains 99.6% water and 0.4% chloroform. The cross sectional area of the column is 0.8 m². Calculate the column height using the following data; kx'.a = 1.35 (kmol/m³.s (Ax)), and ky'.a = 0.06 (kmol/m³.s (Ay)), kx/ky = 1.35, and the equilibrium data are: X 0 0.0133 0.033 y 0 0.01 0.0266 0.049 0.064 0.0747 0.0933 0.1053 0.0433 0.06 0.0733 0.111 0.1 0.12 0.14arrow_forward४ B: Find the numerical solution for the 2D equation below and calculate the temperature values for each grid point shown in Fig. 2 (show all steps). (Do only one trail using following initial values and show the final matrix) [T1] T₂ T3 [T] 1 = [0] 0 0 d dx dx) (ka)+4(ka) = dy -20xy, k = 1 + 0.3 T ge L=3cm, 4x= Ay B.Cs.: at x=0=LT=0°C at y=0-L T=10°C Fig. (2)arrow_forward
- : +0 العنوان use only Two rods fins) having same dimensions, one made orass (k = 85 Wm K) and the mer of copper (k = 375 W/m K), having of their ends inserted into a furna. At a section 10.5 cm a way from furnace, the temperature of brass rod 120 Find the distance at which the ame temperature would be reached in the per rod ? both ends are ex osed to the same environment. ns 2.05 ۲/۱ ostrararrow_forwardFor the beam show below, draw A.F.D, S.F.D, B.M.D 6 kN/m 1 M B. 3 M Marrow_forward1. Two long rods of the same diameter-one made of brass (k=85w/m.k) and the other made of copper (k=375 w/m.k) have one of their ends inserted into a furnace (as shown in the following figure). Both rods are exposed to the same environment. At a distance of 105 mm from the furnace, the temperature of the brass rod is 120°C. At what distance from the furnace will the same temperature be reached in the copper rod? Furnace 105 mm T₁ Brass rod ⑪ h Too- x2- Ti Copper rodarrow_forward
- : +0 العنوان use only Two rods fins) having same dimensions, one made orass (k = 85 Wm K) and the mer of copper (k = 375 W/m K), having of their ends inserted into a furna. At a section 10.5 cm a way from furnace, the temperature of brass rod 120 Find the distance at which the ame temperature would be reached in the per rod ? both ends are ex osed to the same environment. ns 2.05 ۲/۱ ostrararrow_forwardمشر on ۲/۱ Two rods (fins) having same dimensions, one made of brass(k=85 m K) and the other of copper (k = 375 W/m K), having one of their ends inserted into a furnace. At a section 10.5 cm a way from the furnace, the temperature brass rod 120°C. Find the distance at which the same temperature would be reached in the copper rod ? both ends are exposed to the same environment. 22.05 ofthearrow_forwardThe composite wall of oven with A= 1m² as in Fig.1 consists of three materials, two of with kA = 20 W/m K and kc = 50 W/m K with thickness, LA=0.3 m, L= 0.15 m and Lc 0.15 m. The inner surface temperature T1=900 K and the outer surface temperature T4 300 K, and an oven air temperature of To=1100 K, h=25 W/m². K. Determine kɛ and the temperatures T2 and T3 also draw the thermal resistance networkarrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





