
Concept explainers
Often we have distributions of charge for which integrating to find the electric field may not be possible in practice. In such cases, we may be able to get a good approximate solution by dividing the distribution into small but finite particles and taking the vector sum of the contributions of each. To see how this might work, consider a very thin rod of length L = 16 cm with uniform linear charge density λ = 50.0 nC/m. Estimate the magnitude of the electric field at a point P a distance d = 8.0 cm from the end of the rod by dividing it into n segments of equal length as illustrated in Figure P24.21 for n = 4. Treat each segment as a particle whose distance from point P is measured from its center. Find estimates of EP for n = 1, 2, 4, and 8 segments.
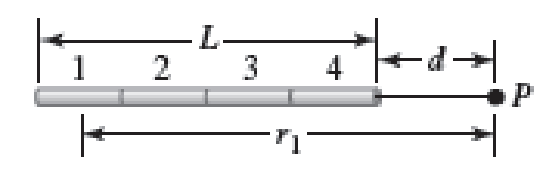
FIGURE P24.21
The magnitudes of electric fields at P for the segments
Answer to Problem 21PQ
The magnitude of electric fields
Explanation of Solution
Write the expression to calculate the electric field.
Here,
Write the expression to calculate the charge in each segment.
Here,
Substitute the above equation in the expression for
Write the expression to calculate
Here, d is the distance of the point P from the end of the rod.
Write the expression to calculate
Write the expression to calculate
Write the expression to calculate
Substitute the equations (II), (III), (IV) and (V) in (I) to rewrite.
Conclusion:
Substitute
Similarly, by following the same concepts the electric field for
Therefore, the magnitude of electric fields
Want to see more full solutions like this?
Chapter 24 Solutions
Webassign Printed Access Card For Katz's Physics For Scientists And Engineers: Foundations And Connections, 1st Edition, Single-term
- Suppose a capacitor consists of two coaxial thin cylindrical conductors. The inner cylinder of radius ra has a charge of +Q, while the outer cylinder of radius rp has charge -Q. The electric field E at a radial distance r from the central axis is given by the function: E = aer/ao + B/r + bo %3D where alpha (a), beta (B), ao and bo are constants. Find an expression for its capacitance. First, let us derive the potential difference Vab between the two conductors. The potential difference is related to the electric field by: Vab = | S"Edr= - [ *Edr Calculating the antiderivative or indefinite integral, Vab = (-aage-r/ao + B + bo By definition, the capacitance C is related to the charge and potential difference by: C = Evaluating with the upper and lower limits of integration for Vab, then simplifying: C = Q/( (e-rb/ao - eralao) + B In( ) + bo ( ))arrow_forwardQUESTION 1 Problem: An infinitely long cylindrical conductor has radius R and uniform surface charge density o. In terms of R and o, what is the charge per unit length A for the cylinder? Answer: A = 2arrow_forwardFill in the blanks.arrow_forward
- A flat wire of infinite length has width W and charge density sigma. If we align the wire so that it is everywhere at y=0 and extends in x from x=d to x=d+L, then calculate the electric field at x=0. Hint: Treat the wire as an the sum of the contributions of many "long wires" where the linear charge density satisfies: lambda=sigma*L.arrow_forwardProblem: An infinitely long cylindrical conductor has radius R and uniform surface charge density O. In terms of Rand O, what is the charge per unit length A for the cylinder? Answer: A = 2arrow_forwardFind the electric field at the origin of the x,y-plane for charge distributions (a) and (b), see the figures shown below. The field is produced (a) by a thin half-circle with a radius of 12.5 cm and the linear charge density K = 18.5 pC/cm and (b) by a thin quarter-circle with the same radius and the linear charge density K = -18.5 pC/cm. K>0 y 0 (a) For the charge distribution (a): The x-component of Ea, Ea,x The y-component of Ea, Ea,y ² For the charge distribution (b): The x-component of Eb, Eb.x = = The y-component of Eb, Eb,y = K<0 Units Select an answer ✓ Units Select an answer ✓ Units Select an answer Units Select an answer 0 (b)arrow_forward
- can you please ans (a) & (b)?arrow_forwardPositive charge is distributed in a sphere of radius R that is centered at the origin. Inside the sphere, the electric field is Ē(r) = kr-1/4 f, where k is a positive constant. There is no charge outside the sphere. a) How is the charge distributed inside the sphere? In particular, find an equation for the charge density, p. b) Determine the electric field, E(r), for r > R (outside the sphere). c) What is the potential difference between the center of the sphere (r = 0) and the surface of the sphere (r = R)? d) What is the energy stored in this electric charge configuration?arrow_forwardA very long line charge having a charge density A is surrounded by a conducting cylindrical shell with inner radius r, = 4.87 cm and outer radius r = 7cm as shown in the figure. System is in electrostatic equilibrium condition. What would be the electric difference AV = V(r=0.55 cm) - V(r= 6.4 cm) ? Provide your answer in terms of Ak with 2 significant figures. potential 6 P Answer:arrow_forward
- A disk with radius R and uniform positive charge density o lies horizontally on a tabletop. A small plastic sphere with mass M and positive charge hovers motionless above the center of the disk, suspended by the Coulomb repulsion due to the charged disk. At what height h does the sphere hover? Express your answer in terms of the dimensionless constant v = 20 Mg/ (Qo). Express your answer in terms of some or all of the variables R and v. h = R- 1-v √(2-v)v Submit Part C h = Previous Answers Correct If M = 300 g, Q = 1.0 μC, R = 6.0 cm, and o = 10 nC/cm², what is h? Express your answer with the appropriate units. μᾶ Value 2 Units Submit Previous Answers Request Answer ? <arrow_forwardcan you please ans (c), (d) & (e)?arrow_forwardWhat is the answerarrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
