Physics for Scientists and Engineers
10th Edition
ISBN: 9781337553278
Author: Raymond A. Serway, John W. Jewett
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 23, Problem 36P
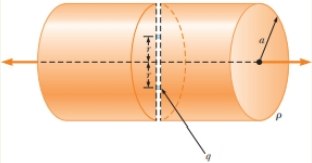
You are working for the summer at a research laboratory. Your research director has devised a scheme for holding small charged particles at fixed positions. The scheme is shown in Figure P23.36. An insulating cylinder of radius a and length L >> a is positively charged and carries a uniform volume charge density ρ. A very thin tunnel is drilled through a diameter of the cylinder and two small spheres with charge q are placed in the tunnel. These spheres are represented by the blue dots in the figure. They find equilibrium positions at a distance of r on opposite sides of the axis of the cylinder. Your research director has had great success with this scheme. (a) Determine the specific value of rat which equilibrium exists. (b) Your research director asks you see if he can extend the system as follows. Determine if it is possible to add transparent plastic tubes as extensions of the tunnel and have the small spheres be in equilibrium at a position for which r > a.
Figure P23.36
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
I FIGURE P27.40 shows a solid metal sphere at the center of a hol-
low metal sphere. What is the total charge on (a) the exterior of
the inner sphere, (b) the inside surface of the hollow sphere, and
(c) the exterior surface of the hollow sphere?
Conducting
spheres
15,000 N/C
5 cm
10 cm
15,000 N/C
cm
8 cm
FIGURE P27.40
17 cm
A wire with a negligible diameter is coaxial with a very thin cylindrical shell of radius R=4.79cm. Both are composed of an insulating material, and for practical purposes, they are infinitely long. The wire has a uniform linear charge density, λ1=−112pC/m, and the cylinder has a linear charge density, λ2=+531pC/m, that is uniformly distributed around its circumference.
a. If r is the distance from the wire, then what is the magnitude, in newtons per coulomb, of the electric field at r=3.08cm.
b. If r is the distance from the wire, then what is the magnitude, in newtons per coulomb, of the electric field at r=8.81cm.
A 3-D printer lays down a semicircular arc of positively charged plastic with a radius R = 2.8 cm, and a linear charge density of λ = +1.6 μC/m. After the printer has finished the arc, the stylus moves to the center of the arc as shown. The minute segment of the plastic arc highlighted in the diagram subtends an angle dθ.
1. Input an expression for the charge dq on the segment of size dθ in terms of given parameters.
2. Input an expression for the electric field vector, dE, generated at the center of the arc by the minute segment of plastic subtending the arc dθ. Express your answer in terms of given parameters, the Coulomb constant k, and the unit vectors i and j.
3. Evaluate the expression from part (b) as an indefinite integral to determine the x-component of the electrical field, Ex, at the center of the arc generated by the entire line of charged plastic.
4. Select the limits of integration that would result in the correct calculation of the electric field at the center of the…
Chapter 23 Solutions
Physics for Scientists and Engineers
Ch. 23.2 - Suppose a point charge is located at the center of...Ch. 23.3 - If the net flux through a gaussian surface is...Ch. 23 - A negatively charged rod of finite length carries...Ch. 23 - A positively charged disk has a uniform charge per...Ch. 23 - A uniformly charged ring of radius 10.0 cm has a...Ch. 23 - The electric field along the axis of a uniformly...Ch. 23 - Example 23.3 derives the exact expression for the...Ch. 23 - A uniformly charged rod of length L and total...Ch. 23 - A continuous line of charge lies along the x axis,...Ch. 23 - A thin rod of length and uniform charge per unit...
Ch. 23 - (a) Consider a uniformly charged, thin-walled,...Ch. 23 - A vertical electric field of magnitude 2.00 104...Ch. 23 - A flat surface of area 3.20 m2 is rotated in a...Ch. 23 - A nonuniform electric field is given by the...Ch. 23 - An uncharged, nonconducting, hollow sphere of...Ch. 23 - Find the net electric flux through the spherical...Ch. 23 - Four closed surfaces, S1 through S4 together with...Ch. 23 - A charge of 170 C is at the center of a cube of...Ch. 23 - (a) Find the net electric flux through the cube...Ch. 23 - A particle with charge of 12.0 C is placed at the...Ch. 23 - A particle with charge Q = 5.00 C is located at...Ch. 23 - A particle with charge Q is located at the center...Ch. 23 - (a) A panicle with charge q is located a distance...Ch. 23 - Find the net electric flux through (a) the closed...Ch. 23 - Figure P23.23 represents the top view of a cubic...Ch. 23 - Determine the magnitude of the electric field at...Ch. 23 - In nuclear fission, a nucleus of uranium-238,...Ch. 23 - Suppose you fill two rubber balloons with air,...Ch. 23 - A large, flat, horizontal sheet of charge has a...Ch. 23 - A nonconducting wall carries charge with a uniform...Ch. 23 - A uniformly charged, straight filament 7.00 m in...Ch. 23 - You are working on a laboratory device that...Ch. 23 - Consider a long, cylindrical charge distribution...Ch. 23 - Assume the magnitude of the electric field on each...Ch. 23 - A solid sphere of radius 40.0 cm has a total...Ch. 23 - A cylindrical shell of radius 7.00 cm and length...Ch. 23 - You are working for the summer at a research...Ch. 23 - You are working for the summer at a research...Ch. 23 - Find the electric flux through the plane surface...Ch. 23 - Three solid plastic cylinders all have radius 2.50...Ch. 23 - A line of charge starts at x = +x0 and extends to...Ch. 23 - Show that the maximum magnitude Emax of the...Ch. 23 - A line of positive charge is formed into a...Ch. 23 - A very large conducting plate lying in the xy...Ch. 23 - A sphere of radius R = 1.00 m surrounds a particle...Ch. 23 - A sphere of radius R surrounds a particle with...Ch. 23 - A slab of insulating material has a nonuniform...Ch. 23 - A sphere of radius 2a is made of a nonconducting...Ch. 23 - An infinitely long insulating cylinder of radius R...Ch. 23 - A particle with charge Q is located on the axis of...Ch. 23 - Review. A slab of insulating material (infinite in...Ch. 23 - Identical thin rods of length 2a carry equal...Ch. 23 - A solid insulating sphere of radius R has a...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- In Figure P24.49, a charged particle of mass m = 4.00 g and charge q = 0.250 C is suspended in static equilibrium at the end of an insulating thread that hangs from a very long, charged, thin rod. The thread is 12.0 cm long and makes an angle of 35.0 with the vertical. Determine the linear charge density of the rod. FIGURE P24.49arrow_forwardThe infinite sheets in Figure P25.47 are both positively charged. The sheet on the left has a uniform surface charge density of 48.0 C/m2, and the one on the right has a uniform surface charge density of 24.0 C/m2. a. What are the magnitude and direction of the net electric field at points A, B, and C? b. What is the force exerted on an electron placed at points A, B, and C? FIGURE P25.47arrow_forwardA thin, semicircular wire of radius R is uniformly charged with total positive charge Q (Fig. P24.63). Determine the electric field at the midpoint O of the diameter.arrow_forward
- A very long, thin wire fixed along the x axis has a linear charge density of 3.2 C/m. a. Determine the electric field at point P a distance of 0.50 m from the wire. b. If there is a test charge q0 = 12.0 C at point P, what is the magnitude of the net force on this charge? In which direction will the test charge accelerate?arrow_forward(a) Find the total electric field at x = 1.00 cm in Figure 18.52(b) given that q =5.00 nC. (b) Find the total electric field at x = 11.00 cm in Figure 18.52(b). (c) If the charges are allowed to move and eventually be brought to rest by friction, what will the final charge configuration be? (That is, will there be a single charge, double charge; etc., and what will its value(s) he?)arrow_forwarda. Figure 24.22A shows a rod of length L and radius R with excess positive charge Q. The excess charge is uniformly distributed over the entire outside surface of the rod. Write an expression for the surface charge density . Write an expression in terms of for the amount of charge dq contained in a small segment of the rod of length dx. b. Figure 24.22B shows a very narrow rod of length L with excess positive charge Q. The rod is so narrow compared to its length that its radius is negligible and the rod is essentially one-dimensional. The excess charge is uniformly distributed over the length of the rod. Write an expression for the linear charge density . Write an expression in terms of for the amount of charge dq contained in a small segment of the rod of length dx. Compare your answers with those for part (a). Explain the similarities and differences.arrow_forward
- A When we find the electric field due to a continuous charge distribution, we imagine slicing that source up into small pieces, finding the electric field produced by the pieces, and then integrating to find the electric field. Lets see what happens if we break a finite rod up into a small number of finite particles. Figure P24.77 shows a rod of length 2 carrying a uniform charge Q modeled as two particles of charge Q/2. The particles are at the ends of the rod. Find an expression for the electric field at point A located a distance above the midpoint of the rod using each of two methods: a. modeling the rod with just two particles and b. using the exact expression E=kQy12+y2 c. Compare your results to the exact expression for the rod by finding the ratio of the approximate expression to the exact expression. FIGURE P24.77 Problems 77 and 78.arrow_forwardFigure P23.49 shows two identical small, charged spheres. One of mass 4.0 g is hanging by an insulating thread of length 20.0 cm. The other is held in place and has charge q1 = 3.6 C. The thread makes an angle of 18 with the vertical, resulting in the spheres being aligned horizontally, a distance r apart. Determine the charge q2 on the hanging sphere. Figure P23.49arrow_forwardThree charged spheres are at rest in a plane as shown in Figure P23.70. Spheres A and B are fixed, but sphere C is attached to the ceiling by a lightweight thread. The tension in the string is 0.240 N. Spheres A and B have charges qA = 28.0 nC and qB = 28.0 nC. What charge is carried by sphere C?arrow_forward
- A circular ring of charge with radius b has total charge q uniformly distributed around it. What is the magnitude of the electric field at the center of the ring? (a) 0 (b) keq/b2 (c) keq2/b2 (d) keq2/b (e) none of those answersarrow_forwardA coaxial cable is formed by a long, straight wire and a hollow conducting cylinder with axes that coincide. The wire has charge per unit length = 20, and the hollow cylinder has net charge per unit length = 30. Use Gausss law to answer these questions: What are the charges per unit length on a. the inner surface and b. the outer surface of the hollow cylinder? c. What is the electric field a radial distance d from the axis of the coaxial cable?arrow_forwardA 2.0 m × 4.0 m flat carpet acquires a uniformly distributed charge of −10 μC after you and your friends walk across it several times. A 2.0 μg dust particle is suspended in midair just above the center of the carpet. A. What is the charge on the dust particle?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning
College Physics
Physics
ISBN:9781938168000
Author:Paul Peter Urone, Roger Hinrichs
Publisher:OpenStax College
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Electric Fields: Crash Course Physics #26; Author: CrashCourse;https://www.youtube.com/watch?v=mdulzEfQXDE;License: Standard YouTube License, CC-BY