
A computer consulting firm presently has bids out on three projects. Let Ai = {awarded project i}, for i = 1, 2, 3, and suppose that P(A1) = .22, P(A2) = .25, P(A3) = .28, P(A1 ∩ A2) = .11, P(A1 ∩ A3) = .05, P(A2 ∩ A3) = .07, P(A1 ∩ A2 ∩ A3) = .01. Express in words each of the following events, and compute the
- a. A1 ∪ A2
- b. A1′∩ A2′ [Hint: (A1 ∪ A2)′ = A′1 ∩ A′2]
- c. A1 ∪ A2 ∪ A3
- d. A′1 ∩ A′2 ∩ A′3
- e. A′1 ∩ A′2 ∩ A3
- f. (A′1 ∩ A′2 ) ∪ A3
a.
Compute
Answer to Problem 13E
The probability of an event
Explanation of Solution
Given info:
The data represents the projects of the consulting firm.
Here, A1 be awarded project 1,
A2 be awarded project 2,
A3 be awarded project .
Let
Calculation:
Addition rule:
For any two events A and B,
Complement:
The complement of the event A contains the set of all element that are contained in sample space S and not contained in event A. it is denoted as
Union:
The union of two events A1 or A2 contains set of all elements which are either in A1, A2, or both the events. It is denoted by
Intersection:
The intersection of two event A1 and A2 contains set all of element which are in both A1 and A2. It is denoted by
The probability of A1 or A2 can be obtained as
Thus, the probability of an event
b.
Compute
Answer to Problem 13E
The probability of an event
Explanation of Solution
Calculation:
The probability of
The event
Thus, the probability of an event
c.
Compute
Answer to Problem 13E
The probability of an event
Explanation of Solution
Calculation:
Addition rule:
For any three events A, B and C ,
The event
The probability of
Thus, the probability of an event
d.
Compute
Answer to Problem 13E
The probability of an event
Explanation of Solution
Calculation:
The event
The probability of
Thus, the probability of an event
e.
Compute
Answer to Problem 13E
The probability of an event
Explanation of Solution
Calculation:
The event
The event
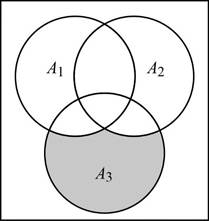
From the Venn diagram, the probability of
Thus, the probability of an event
f.
Compute
Answer to Problem 13E
The probability of an event
Explanation of Solution
Calculation:
The event
The event
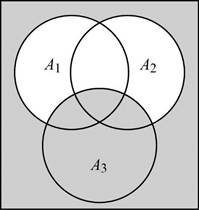
The probability of
Thus, the probability of an event
Want to see more full solutions like this?
Chapter 2 Solutions
Probability and Statistics for Engineering and the Sciences
- 2. Suppose that in Example 2.27, 400 units of food A, 500 units of B, and 600 units of C are placed in the test tube each day and the data on daily food consumption by the bacteria (in units per day) are as shown in Table 2.7. How many bacteria of each strain can coexist in the test tube and consume all of the food? Table 2.7 Bacteria Strain I Bacteria Strain II Bacteria Strain III Food A 1 2 0 Food B 2 1 3 Food C 1 1 1arrow_forwardA computer consulting firm presently has bids out on three projects. Let Ai = {awarded project i}, for i = 1, 2, 3, and suppose that P(A1) = 0.23, P(A2) = 0.25, P(A3) = 0.29, P(A1 ∩ A2) = 0.08, P(A1 ∩ A3) = 0.05, P(A2 ∩ A3) = 0.07, P(A1 ∩ A2 ∩ A3) = 0.01. Use the probabilities given above to compute the following probabilities, and explain in words the meaning of each one. (Round your answers to four decimal places.) P(A1 ∩ A2 ∩ A3 | A1 ∪ A2 ∪ A3)arrow_forwardA computer consulting firm presently has bids out on three projects. Let Ai = {awarded project i}, for i = 1, 2, 3, and suppose that P(A1) = 0.23, P(A2) = 0.25, P(A3) = 0.28, P(A1 ∩ A2) = 0.09, P(A1 ∩ A3) = 0.08, P(A2 ∩ A3) = 0.05, P(A1 ∩ A2 ∩ A3) = 0.01. Use the probabilities given above to compute the following probabilities, and explain in words the meaning of each one. (Round your answers to four decimal places.) (a) P(A2 | A1) = Explain this probability in words. This is the probability that the firm is awarded either project 1 or project 2.If the firm is awarded project 2, this is the chance they will also be awarded project 1. If the firm is awarded project 1, this is the chance they will also be awarded project 2.This is the probability that the firm is awarded both project 1 and project 2. (b) P(A2 ∩ A3 | A1) = Explain this probability in words. If the firm is awarded project 1, this is the chance they will also be awarded projects 2 and 3.This is the probability that…arrow_forward
- A computer consulting firm presently has bids out on three projects. Let Ai = {awarded project i}, for i = 1, 2, 3, and suppose that P(A1) = 0.22, P(A2) = 0.26, P(A3) = 0.28, P(A1 ∩ A2) = 0.07, P(A1 ∩ A3) = 0.09, P(A2 ∩ A3) = 0.08, P(A1 ∩ A2 ∩ A3) = 0.01. Use the probabilities given above to compute the following probabilities. (Round your answers to four decimal places.) (a) P(A2 ∩ A3 | A1) (b) P(A2 ∪ A3 | A1) Please use typefont and explain the steps clearly. Thank you!arrow_forwardA computer consulting firm presently has bids out on three projects. Let A₁ = {awarded project /}, for i = 1, 2, 3, and suppose that P(A₂) = 0.23, P(A₂) = 0.26, P(A3) = 0.29, P(A₁A₂) = 0.11, P(A₁ A₂) = 0.05, P(A₂ A3) = 0.08, P(A₁ A₂ A3) = 0.01. Use the probabilities given above to compute the following probabilities, and explain in words the meaning of each one. (Round your answers to four decimal places.) (a) P(A₂|A₂₁) = Explain this probability in words. O This is the probability that the firm is awarded either project 1 or project 2. O This is the probability that the firm is awarded both project 1 and project 2. O If the firm is awarded project 1, this is the chance they will also be awarded project 2. O If the firm is awarded project 2, this is the chance they will also be awarded project 1. (b) P(A₂A₂A₂) = Explain this probability in words. O This is the probability that the firm is awarded at least one of the projects. O This is the probability that the firm is awarded projects…arrow_forwardA computer consulting firm presently has bids out on three projects. Let A; = {awarded project i}, for i= 1, 2, 3, and suppose that P(A₁) = 0.23, P(A₂) = 0.26, P(A3) = 0.28, P(A₁ A₂) = 0.08, P(A₁ A₂) = 0.07, P(A₂n A3) = 0.05, P(A₁ A₂ A3) = 0.02. Use the probabilities given above to compute the following probabilities, and explain in words the meaning of each one. (Round your answers to four decimal places.) (a) P(A₂|A₁₂) = | Explain this probability in words. O If the firm is awarded project 2, this is the chance they will also be awarded project 1. O This is the probability that the firm is awarded either project 1 or project 2. O If the firm is awarded project 1, this is the chance they will also be awarded project 2. O This is the probability that the firm is awarded both project 1 and project 2. (b) P(A₂n A3 A₁) =| Explain this probability in words. O This is the probability that the firm is awarded projects 1, 2, and 3. O This is the probability that the firm is awarded at least…arrow_forward
- A computer consulting firm presently has bids out on three projects. Let Ai= {awarded project i}, for i = 1, 2, 3, and suppose that P(A1) = 0.22, P(A2) = 0.25, P(A3) = 0.28, P(A1 \cap A2) = 0.12, P(A1 \cap A3) = 0.04, P(A2 \cap A 3) = 0.05, P(A1 \cap A2 \cap A3) = 0.01. Compute the probability of each event.arrow_forwardAn IT company is planning to introduce a new product. In order to predict its sales, they release the test version of the product to a group of early-access users. Each user is asked to give a score for the product from 0 to 100. If a user's score is greater than 50, then the user is classified as a potential buyer. a) Suppose you are a researcher and can collect any data as you wish. Briefly discuss what data you would collect, and how you would collect them. What distribution would be the best choice to model the score? What distribution would be the best choice to model being a potential buyer? Be sure to define random variables clearly. Give reasons for your answer. b) The manager decided that if more than 80% of users are classified as potential buyers, they will release the product. How would you conduct a hypothesis test? Make assumptions if you need. Please give some detailed reasons, i will be very very appreciate!!!!!arrow_forwardStudents at certain university have to pass of one these three courses (MAT102, STA105, and PHY110). The pass rates for the courses MAT 102, STA105, and PHY110 are 0.54, 0.79, and 0.86, respectively. Suppose that 30 candidates take the MAT102 course, 25 take the STA105 course and 20 take the PHY110 coruse. A student takes one of these courses and passes. What are the probabilities that she took MAT102, STA105 or PHY110? Hint: Denote by Q the event a student to pass their course. Now denote by R1, R2 and R3 the events to take courses MAT102, STA105, and PHY110. The pass reates then represent the conditional probabilites: P(Q| R1), P(Q| R2) and P(Q| R3). The number of students taking the courses can be used to estimate the probabilities for R1, R2 and R3. For example, since there are total of 30 + 25 + 20 = 75 students that take the courses, for R1 we have: P(R1) = 30/75 = 2/5 What you are asked is: given that a student passes (event Q) estimate the probabilities that she took MAT102…arrow_forward
- If q= (5p1+3p2) / (p1+p2) find dq/dp1 and dq/dp2arrow_forwardYou are playing a single joint game with all your fellow students where you have to choose an integer from (0,1,2, .100}. A player's payoff depends on the distance of his answer to 2/3 of the average of all players' answers; the closer the better. Example: Your answer is 45. There are two other players whose answers are 25 and 56. Then, the average is (45+25+56)/3=42. 2/3 of the average is 28. Your distance to 2/3 of the average is 145-28|=17. All players will be ranked according to their answer's proximity to 2/3 of the average. The top 25% of the players get 2 points. The next 50% get 1 point. The bottom 25% get 0 points. (In case of ties, points will be distributed evenly in the enlarged classes.) Please give your answer as a single integer from (0,1,2,3,.100}. A valid submission would look like this: 45arrow_forwardThere is a chance that a bit transmitted through a digital transmission channel is received in error. Let X equal the number of bits in error in the next four bits transmitted. The possible values of X are {0,1,2,3}. Suppose that P(X=0)=0.6, P(X=1)= 0.3, P(X=2)= 0.05, P(X=3)= 0.05 What is the CDF of X at 3? i.e., what is F(3)? a). 0.6 b). 0.9 c). 0.95 d). 1 e). none of above For the random variable defined in question 12, if we know that Var(X)=0.6475, what is the standard deviation of X? a). 0.55 b). 0.6475 c). 0.419 d). 0.8 e). none of abovearrow_forward
 Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill

