A Transition to Advanced Mathematics
8th Edition
ISBN: 9781285463261
Author: Douglas Smith, Maurice Eggen, Richard St. Andre
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 2.1, Problem 19E
Repeat Exercise 2 with the operation * given by the table on the right.
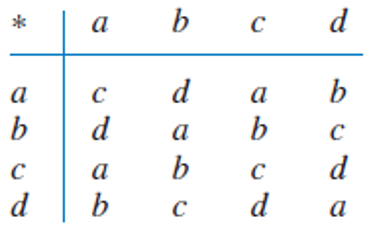
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Let A be a vector space with basis 1, a, b. Which (if any) of the following rules
turn A into an algebra? (You may assume that 1 is a unit.)
(i) a² = a, b² = ab = ba = 0.
(ii) a²=b, b² = ab = ba = 0.
(iii) a²=b, b² = b, ab = ba = 0.
No chatgpt pls will upvote
= 1. Show
(a) Let G = Z/nZ be a cyclic group, so G = {1, 9, 92,...,g" } with g":
that the group algebra KG has a presentation KG = K(X)/(X” — 1).
(b) Let A = K[X] be the algebra of polynomials in X. Let V be the A-module
with vector space K2 and where the action of X is given by the matrix
Compute End(V) in the cases
(i) x = p,
(ii) xμl.
(67) ·
(c) If M and N are submodules of a module L, prove that there is an isomorphism
M/MON (M+N)/N.
(The Second Isomorphism Theorem for modules.)
You may assume that MON is a submodule of M, M + N is a submodule of L
and the First Isomorphism Theorem for modules.
Chapter 2 Solutions
A Transition to Advanced Mathematics
Ch. 2.1 - The Cayley tables for operations o,*,+, and are...Ch. 2.1 - Let m,n and M=A:A is an mn matrix with real number...Ch. 2.1 - Let be an associative operation on nonempty set A...Ch. 2.1 - Let be an associative operation on nonempty set A...Ch. 2.1 - Suppose that (A,*) is an algebraic system and * is...Ch. 2.1 - Let (A,o) be an algebra structure. An element lA...Ch. 2.1 - Let G be a group. Prove that if a2=e for all aG,...Ch. 2.1 - Give an example of an algebraic structure of order...Ch. 2.1 - Prob. 9ECh. 2.1 - Construct the operation table for each of the...
Ch. 2.1 - Prob. 11ECh. 2.1 - Prob. 12ECh. 2.1 - Suppose m and m2. Prove that 1 and m1 are distinct...Ch. 2.1 - Let m and a be natural numbers with am. Complete...Ch. 2.1 - Complete the proof of Theorem 6.1.4. First, show...Ch. 2.1 - Prob. 16ECh. 2.1 - Prob. 17ECh. 2.1 - Prob. 18ECh. 2.1 - Repeat Exercise 2 with the operation * given by...Ch. 2.2 - Prob. 1ECh. 2.2 - Let G be a group and aiG for all n. Prove that...Ch. 2.2 - Prove part (d) of Theorem 6.2.3. That is, prove...Ch. 2.2 - Prove part (b) of Theorem 6.2.4.Ch. 2.2 - List all generators of each cyclic group in...Ch. 2.2 - Let G be a group with identity e. Let aG. Prove...Ch. 2.2 - Let G be a group, and let H be a subgroup of G....Ch. 2.2 - Let ({0},) be the group of nonzero complex numbers...Ch. 2.2 - Prove that for every natural number m greater than...Ch. 2.2 - Show that the structure ({1},), with operation ...Ch. 2.2 - (a)In the group G of Exercise 2, find x such that...Ch. 2.2 - Show that (,), with operation # defined by...Ch. 2.2 - Prob. 13ECh. 2.2 - Prob. 14ECh. 2.2 - Prob. 15ECh. 2.2 - Show that each of the following algebraic...Ch. 2.2 - Prob. 17ECh. 2.2 - Given that G={e,u,v,w} is a group of order 4 with...Ch. 2.2 - Give an example of an algebraic system (G,o) that...Ch. 2.2 - (a)What is the order of S4, the symmetric group on...Ch. 2.3 - Find the order of the element 3 in each group....Ch. 2.3 - Find the order of each element of the group S3....Ch. 2.3 - Let 3 and 6 be the sets of integer multiples of 3...Ch. 2.3 - Let (3,+) and (6,+) be the groups in Exercise 10,...Ch. 2.3 - Let ({a,b,c},o) be the group with the operation...Ch. 2.3 - (a)Prove that the function f:1824 given by f(x)=4x...Ch. 2.3 - Define f:1512 by f(x)=4x. Prove that f is a...Ch. 2.3 - Let (G,) and (H,*) be groups, i be the identity...Ch. 2.3 - Show that (4,+) and ({1,1,i,i},) are isomorphic.Ch. 2.3 - Prove that every subgroup of a cyclic group is...Ch. 2.3 - Let G=a be a cyclic group of order 30. What is the...Ch. 2.3 - Assign a grade of A (correct), C (partially...Ch. 2.3 - Find all subgroups of (8,+). (U11,). (5,+). (U7,)....Ch. 2.3 - In the group S4, find two different subgroups that...Ch. 2.3 - Prove that if G is a group and H is a subgroup of...Ch. 2.3 - (a)Prove that if H and K are subgroups of a group...Ch. 2.3 - Let G be a group and H be a subgroup of G. If H is...Ch. 2.3 - Prove or disprove: Every abelian group is cyclic.Ch. 2.3 - Let G be a group. If H is a subgroup of G and K is...Ch. 2.4 - Define f:++ by f(x)=x where + is the set of all...Ch. 2.4 - Assign a grade of A (correct), C (partially...Ch. 2.4 - Define f: by f(x)=x3. Is f:(,+)(,+) operation...Ch. 2.4 - Define on by setting (a,b)(c,d)=(acbd,ad+bc)....Ch. 2.4 - Let f the set of all real-valued integrable...Ch. 2.4 - Prob. 6ECh. 2.4 - Let M be the set of all 22 matrices with real...Ch. 2.4 - Let Conj: be the conjugate mapping for complex...Ch. 2.4 - Prove the remaining parts of Theorem 6.4.1.Ch. 2.4 - Is S3 isomorphic to (6,+)? Explain.Ch. 2.4 - Prob. 11ECh. 2.4 - Use the method of proof of Cayley's Theorem to...Ch. 2.5 - Let (R,+,) be an algebraic structure such that...Ch. 2.5 - Assign a grade of A (correct), C (partially...Ch. 2.5 - Which of the following is a ring with the usual...Ch. 2.5 - Let [2] be the set {a+b2:a,b}. Define addition and...Ch. 2.5 - Complete the proof that for every m,(m+,) is a...Ch. 2.5 - Define addition and multiplication on the set ...Ch. 2.5 - Prob. 7ECh. 2.5 - Let (R,+,) be a ring and a,b,R. Prove that b+(a)...Ch. 2.5 - Prove the remaining parts of Theorem 6.5.3: For...Ch. 2.5 - Prob. 10ECh. 2.5 - Prob. 11ECh. 2.5 - Prob. 12ECh. 2.5 - Prob. 13ECh. 2.5 - Prob. 14ECh. 2.6 - Prob. 1ECh. 2.6 - Let A and B be subsets of . Prove that if sup(A)...Ch. 2.6 - (a)Give an example of sets A and B of real numbers...Ch. 2.6 - (a)Give an example of sets A and B of real numbers...Ch. 2.6 - Prob. 5ECh. 2.6 - Prob. 6ECh. 2.6 - Prob. 7ECh. 2.6 - Prob. 8ECh. 2.6 - Prob. 9ECh. 2.6 - Prob. 10ECh. 2.6 - Prob. 11ECh. 2.6 - Prob. 12ECh. 2.6 - Prob. 13ECh. 2.6 - Prob. 14ECh. 2.6 - Prob. 15ECh. 2.6 - Prob. 16ECh. 2.6 - Use the definition of “divides” to explain (a) why...Ch. 2.6 - Prob. 18ECh. 2.6 - Prob. 19ECh. 2.6 - Prob. 20ECh. 2.6 - For each function, find the value of f at 3 and...Ch. 2.6 - Let A be the set {1,2,3,4} and B={0,1,2,3}. Give a...Ch. 2.6 - Formulate and prove a characterization of greatest...Ch. 2.6 - Prob. 24ECh. 2.6 - Prob. 25E
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
- (a) Define the notion of an ideal I in an algebra A. Define the product on the quotient algebra A/I, and show that it is well-defined. (b) If I is an ideal in A and S is a subalgebra of A, show that S + I is a subalgebra of A and that SnI is an ideal in S. (c) Let A be the subset of M3 (K) given by matrices of the form a b 0 a 0 00 d Show that A is a subalgebra of M3(K). Ꮖ Compute the ideal I of A generated by the element and show that A/I K as algebras, where 0 1 0 x = 0 0 0 001arrow_forward(a) Let HI be the algebra of quaternions. Write out the multiplication table for 1, i, j, k. Define the notion of a pure quaternion, and the absolute value of a quaternion. Show that if p is a pure quaternion, then p² = -|p|². (b) Define the notion of an (associative) algebra. (c) Let A be a vector space with basis 1, a, b. Which (if any) of the following rules turn A into an algebra? (You may assume that 1 is a unit.) (i) a² = a, b²=ab = ba 0. (ii) a² (iii) a² = b, b² = abba = 0. = b, b² = b, ab = ba = 0. (d) Let u1, 2 and 3 be in the Temperley-Lieb algebra TL4(8). ገ 12 13 Compute (u3+ Augu2)² where A EK and hence find a non-zero x € TL4 (8) such that ² = 0.arrow_forwardQ1: Solve the system x + x = t², x(0) = (9)arrow_forward
- Between the function 3 (4)=x-x-1 Solve inside the interval [1,2]. then find the approximate Solution the root within using the bisection of the error = 10² method.arrow_forwardE10) Perform four iterations of the Jacobi method for solving the following system of equations. 2 -1 -0 -0 XI 2 0 0 -1 2 X3 0 0 2 X4 With x(0) (0.5, 0.5, 0.5, 0.5). Here x = (1, 1, 1, 1)". How good x (5) as an approximation to x?arrow_forwardby (2) Gauss saidel - - method find (2) و X2 for the sestem X1 + 2x2=-4 2x1 + 2x2 = 1 Such thef (0) x2=-2arrow_forward
- ax+b proof that se = - è (e" -1)" ë naxarrow_forward20.11 ← UAS Sisa waktu 01:20:01 51%- Soal 2 Perhatikan gambar di bawah (Sembunyikan ) Belum dijawab Ditandai dari 1,00 5 A B E D 10 20 Jika ruas garis AB, PE, dan DC sejajar dan ketiganya tegak lurus dengan ruas garis BC, maka panjang ruas garis PE adalah ... (cukup tulis bilangannya tanpa spasi dalam bentuk desimal tiga angka di belakang koma, seperti a,bcd atau pecahan m/n untuk m n Jawaban: Jawaban ||| <arrow_forward20.07 52% X https://www.chegg.com/hc <: C Chegg Learn on the go = Chegg (X) Open in app EN-US ✔ What's your next question? √x #16 A surveyor sees a building across the river. Standing at point A he measures the angle of elevation from the ground to the top of the building to be 30 degrees. He steps back 100 feet and again measures the angle of elevation and finds it to be 15. (See Figure 12.26.) Assuming that it makes a 90-degree angle with the floor, approximately how tall is the building? 15 30° 100 A river Figure 12.26 Show image transcript Here's the best way to solve it. Solution ||| о building < Sharearrow_forward
- No chatgpt pls will upvotearrow_forwardModule Code: MATH380202 3. (a) Let {} be a white noise process with variance σ2. Define an ARMA(p,q) process {X} in terms of {+} and state (without proof) conditions for {X} to be (i) weakly stationary and (ii) invertible. Define what is meant by an ARIMA (p, d, q) process. Let {Y} be such an ARIMA(p, d, q) process and show how it can also be represented as an ARMA process, giving the AR and MA orders of this representation. (b) The following tables show the first nine sample autocorrelations and partial auto- correlations of X and Y₁ = VX+ for a series of n = 1095 observations. (Notice that the notation in this part has no relationship with the notation in part (a) of this question.) Identify a model for this time series and obtain preliminary estimates for the pa- rameters of your model. X₁ = 15.51, s² = 317.43. k 1 2 3 4 5 6 7 Pk 0.981 0.974 0.968 akk 0.981 0.327 8 9 0.927 0.963 0.957 0.951 0.943 0.935 0.121 0.104 0.000 0.014 -0.067 -0.068 -0.012 Y₁ = VX : y = 0.03, s² = 11.48. k 1…arrow_forwardLet G be a graph with n ≥ 2 vertices x1, x2, . . . , xn, and let A be the adjacency matrixof G. Prove that if G is connected, then every entry in the matrix A^n−1 + A^nis positive.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Elementary AlgebraAlgebraISBN:9780998625713Author:Lynn Marecek, MaryAnne Anthony-SmithPublisher:OpenStax - Rice University
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Intermediate AlgebraAlgebraISBN:9781285195728Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Elementary Algebra
Algebra
ISBN:9780998625713
Author:Lynn Marecek, MaryAnne Anthony-Smith
Publisher:OpenStax - Rice University
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Intermediate Algebra
Algebra
ISBN:9781285195728
Author:Jerome E. Kaufmann, Karen L. Schwitters
Publisher:Cengage Learning
Mod-01 Lec-01 Discrete probability distributions (Part 1); Author: nptelhrd;https://www.youtube.com/watch?v=6x1pL9Yov1k;License: Standard YouTube License, CC-BY
Discrete Probability Distributions; Author: Learn Something;https://www.youtube.com/watch?v=m9U4UelWLFs;License: Standard YouTube License, CC-BY
Probability Distribution Functions (PMF, PDF, CDF); Author: zedstatistics;https://www.youtube.com/watch?v=YXLVjCKVP7U;License: Standard YouTube License, CC-BY
Discrete Distributions: Binomial, Poisson and Hypergeometric | Statistics for Data Science; Author: Dr. Bharatendra Rai;https://www.youtube.com/watch?v=lHhyy4JMigg;License: Standard Youtube License