Chapter 19, Problem 55E

(a)

To determine

The direction and the magnitude of the acceleration of an electron.

Answer to Problem 55E

The magnitude of the acceleration is $\frac{evB}{2m}$ and the direction is normal to the magnetic field.

Explanation of Solution

Write the expression for Newton’s law of motion.

    $F=mf$        (1)

Here, $F$ is the magnitude of force, $m$ is the mass and $f$ is the acceleration of a particle.

Write the expression of the component of velocity along the acceleration.

    $v_1=v\sin \left(\theta \right)$

Here, $v_1$ is the component of the velocity perpendicular to the magnetic field, $v$ is the velocity and $\theta$ is the angle between the projectile direction and field.

Write the expression force on a particle ion magnetic field.

    $F=e{v}_{1}B$

Here, $e$ is the charge of the particle and $B$ is the magnetic field.

Substitute $v\sin \left(\theta \right)$ for $v_1$ in the above equation.

    $F=e\left(v\sin \left(\theta \right)\right)B$        (2)

Compare equation (1) and (2).

    $\begin{array}{c}mf=e\left(v\sin \left(\theta \right)\right)B\\ f=\frac{eBv\sin \left(\theta \right)}{m}\end{array}$        (3)

Conclusion:

Substitute $30°$ for $\theta$ in equation (3).

    $\begin{array}{c}f=\frac{evB\sin \left(30°\right)}{2m}\\ =\frac{evB}{2m}\end{array}$

Thus, the magnitude of the acceleration is $\frac{evB}{2m}$ and the direction is normal to the magnetic field.

(b)

To determine

The component of the velocity along the magnetic field.

Answer to Problem 55E

The component of the velocity along the field is $0.866v$ and the change of velocity along the direction of magnetic field is zero..

Explanation of Solution

Write the expression of the component of velocity along the field.

    $v_2=v\cos \left(\theta \right)$        (4)

Here, $v_2$ is the component of the velocity along the field, $v$ is the projectile velocity and $\theta$ is the angle between the projectile direction and field.

Conclusion:

Substitute $30°$ for $\theta$ in equation (4).

    $\begin{array}{c}{v}_2=v\cos \left(30°\right)\\ =0.866v\end{array}$

Thus, the component of the velocity along the field is $0.866v$ and the velocity is changed in the direction perpendicular to the field, so the change of velocity along the direction of magnetic field is zero.

(c)

To determine

The velocity along the along the direction perpendicular to the field and the radius of the path.

Answer to Problem 55E

The component of the velocity along the perpendicular direction to the magnetic field is $\frac{v}{2}$ and the radius of the path is $\frac{mv}{2eB}$.

Explanation of Solution

Write the expression of the component of velocity along the perpendicular direction to the magnetic field.

    $v_1=v\sin \left(\theta \right)$        (5)

Write the expression for the radius of the path.

    $r=\frac{m{v}_1}{eB}$

Here, $r$ is the radius of the path.

Substitute $v\sin \left(\theta \right)$ for $v_1$ in the above equation.

    $r=\frac{mv\sin \left(\theta \right)}{eB}$        (6)

Conclusion:

Substitute $30°$ for $\theta$ in equation (6).

    $\begin{array}{c}r=\frac{mv\sin \left(30°\right)}{eB}\\ =\frac{mv}{2eB}\end{array}$

Thus, the component of the velocity along the perpendicular direction to the magnetic field is $\frac{v}{2}$ and the radius of the path is $\frac{mv}{2eB}$.

(d)

To determine

The distance of the electron for one full rotation.

Answer to Problem 55E

The distance covered by an electron along the direction of magnetic field is $1.732\frac{\pi mv}{eB}$.

Explanation of Solution

Write the expression for the radius of the path along the direction of field.

    $r=\frac{m{v}_2}{eB}$        (7)

Write the expression of the component of velocity along the field.

    $v_2=v\cos \left(\theta \right)$

Substitute $v\cos \left(\theta \right)$ for $v_2$ in equation (7).

    $r=\frac{mv\cos \left(\theta \right)}{eB}$        (8)

Write the expression for the distance of the electron.

    $l=2\pi r$        (9)

Here, $l$ is the distance of the electron for a full cycle.

Conclusion:

Substitute $30°$ for $\theta$ in equation (8).

    $\begin{array}{c}r=\frac{mv\cos \left(30°\right)}{eB}\\ =0.866\frac{mv}{eB}\end{array}$

Substitute $0.866\frac{mv}{eB}$ for $r$ in equation (9).

    $\begin{array}{c}l=2\pi \left(0.866\frac{mv}{eB}\right)\\ =1.732\frac{\pi mv}{eB}\end{array}$

Thus, the distance covered by an electron along the direction of magnetic field is $1.732\frac{\pi mv}{eB}$.

(e)

To determine

The nature of the path of electron.

Answer to Problem 55E

The path of the electron is helix.

Explanation of Solution

Use right hand rule to sketch the trajectory of the electron.

The trajectory of the electron in the magnetic field is sketched.

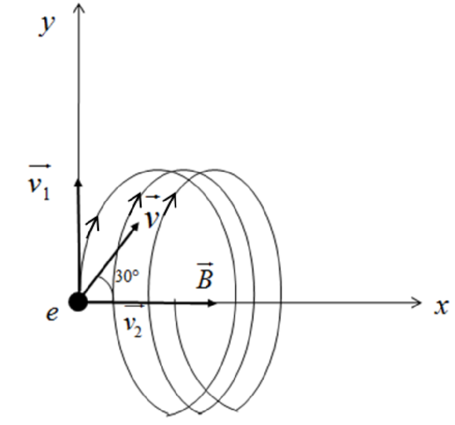
Conclusion:

Thus, the path of the electron is helix.