
Starting Out with C++: Early Objects (9th Edition)
9th Edition
ISBN: 9780134400242
Author: Tony Gaddis, Judy Walters, Godfrey Muganda
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Expert Solution & Answer
Chapter 19, Problem 1RQE
Program Description Answer
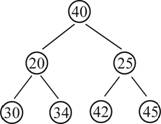
The first node in binary tree is referred as “root node”.
Expert Solution & Answer
Explanation of Solution
Binary tree:
A complete binary tree is a binary tree with the property that every node must have exactly two children, and at the last level the nodes should be from left to right.
Root node:
- First node must be the root of the tree.
- The second node must be the left child of the root
- The third node must always be the right child of the root.
- The next node must start to fill the next level from left to right.
The diagrammatic representation of binary tree is as follows:
Want to see more full solutions like this?
Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!
Students have asked these similar questions
Make the following game user friendly with GUI, with some simple graphics. The GUI should be in another seperate class, with some ImageIcon, and Game class should be added into the pane.
The following code works as this: The objective of the player is to escape from this labyrinth. The player starts at the bottom left corner of the labyrinth. He has to get to the top right corner of the labyrinth as fast he can, avoiding a meeting with the evil dragon. The player can move only in four directions: left, right, up or down. There are several escape paths in all labyrinths. The player’s character should be able to moved with the well known WASD keyboard buttons. If the dragon gets to a neighboring field of the player, then the player dies. Because it is dark in the labyrinth, the player can see only the neighboring fields at a distance of 3 units.
Cell Class:
public class Cell { private boolean isWall; public Cell(boolean isWall) { this.isWall = isWall; } public boolean isWall() { return…
Discuss the negative and positive impacts or information technology in the context of your society. Provide two references along with with your answer
A cylinder of diameter 10 cm rotates concentrically inside another hollow
cylinder of inner diameter 10.1 cm. Both cylinders are 20 cm long and stand with their
axis vertical. The annular space is filled with oil. If a torque of 100 kg cm is required to
rotate the inner cylinder at 100 rpm, determine the viscosity of oil. Ans. μ= 29.82poise
Chapter 19 Solutions
Starting Out with C++: Early Objects (9th Edition)
Ch. 19.1 - Prob. 19.1CPCh. 19.1 - Prob. 19.2CPCh. 19.1 - Prob. 19.3CPCh. 19.1 - Prob. 19.4CPCh. 19.1 - Prob. 19.5CPCh. 19.1 - Prob. 19.6CPCh. 19.2 - Prob. 19.7CPCh. 19.2 - Prob. 19.8CPCh. 19.2 - Prob. 19.9CPCh. 19.2 - Prob. 19.10CP
Ch. 19.2 - Prob. 19.11CPCh. 19.2 - Prob. 19.12CPCh. 19 - Prob. 1RQECh. 19 - Prob. 2RQECh. 19 - Prob. 3RQECh. 19 - Prob. 4RQECh. 19 - Prob. 5RQECh. 19 - Prob. 6RQECh. 19 - Prob. 7RQECh. 19 - Prob. 8RQECh. 19 - Prob. 9RQECh. 19 - Prob. 10RQECh. 19 - Prob. 11RQECh. 19 - Prob. 12RQECh. 19 - Prob. 13RQECh. 19 - Prob. 14RQECh. 19 - Prob. 15RQECh. 19 - Prob. 16RQECh. 19 - Prob. 17RQECh. 19 - Prob. 18RQECh. 19 - Prob. 19RQECh. 19 - Prob. 20RQECh. 19 - Prob. 1PCCh. 19 - Prob. 2PCCh. 19 - Prob. 3PCCh. 19 - Prob. 4PCCh. 19 - Prob. 5PCCh. 19 - Prob. 6PCCh. 19 - Prob. 7PCCh. 19 - Prob. 8PCCh. 19 - Prob. 9PCCh. 19 - Prob. 10PC
Knowledge Booster
Similar questions
- Make the following game user friendly with GUI, with some simple graphics The following code works as this: The objective of the player is to escape from this labyrinth. The player starts at the bottom left corner of the labyrinth. He has to get to the top right corner of the labyrinth as fast he can, avoiding a meeting with the evil dragon. The player can move only in four directions: left, right, up or down. There are several escape paths in all labyrinths. The player’s character should be able to moved with the well known WASD keyboard buttons. If the dragon gets to a neighboring field of the player, then the player dies. Because it is dark in the labyrinth, the player can see only the neighboring fields at a distance of 3 units. Cell Class: public class Cell { private boolean isWall; public Cell(boolean isWall) { this.isWall = isWall; } public boolean isWall() { return isWall; } public void setWall(boolean isWall) { this.isWall = isWall; } @Override public String toString() {…arrow_forwardPlease original work What are four of the goals of information lifecycle management think they are most important to data warehousing, Why do you feel this way, how dashboards can be used in the process, and provide a real life example for each. Please cite in text references and add weblinksarrow_forwardThe following is code for a disc golf program written in C++: // player.h #ifndef PLAYER_H #define PLAYER_H #include <string> #include <iostream> class Player { private: std::string courses[20]; // Array of course names int scores[20]; // Array of scores int gameCount; // Number of games played public: Player(); // Constructor void CheckGame(int playerId, const std::string& courseName, int gameScore); void ReportPlayer(int playerId) const; }; #endif // PLAYER_H // player.cpp #include "player.h" #include <iomanip> Player::Player() : gameCount(0) {} void Player::CheckGame(int playerId, const std::string& courseName, int gameScore) { for (int i = 0; i < gameCount; ++i) { if (courses[i] == courseName) { // If course has been played, then check for minimum score if (gameScore < scores[i]) { scores[i] = gameScore; // Update to new minimum…arrow_forward
- In this assignment, you will implement a multi-threaded program (using C/C++) that will check for Prime Numbers and Palindrome Numbers in a range of numbers. Palindrome numbers are numbers that their decimal representation can be read from left to right and from right to left (e.g. 12321, 5995, 1234321). The program will create T worker threads to check for prime and palindrome numbers in the given range (T will be passed to the program with the Linux command line). Each of the threads works on a part of the numbers within the range. Your program should have some global shared variables: • numOfPrimes: which will track the total number of prime numbers found by all threads. numOfPalindroms: which will track the total number of palindrome numbers found by all threads. numOfPalindromic Primes: which will count the numbers that are BOTH prime and palindrome found by all threads. TotalNums: which will count all the processed numbers in the range. In addition, you need to have arrays…arrow_forwardHow do you distinguish between hardware and a software problem? Discuss theprocedure for troubleshooting any hardware or software problem. give one reference with your answer.arrow_forwardYou are asked to explain what a computer virus is and if it can affect computer’shardware or software. How do you protect your computer against virus? give one reference with your answer.arrow_forward
- Distributed Systems: Consistency Models fer to page 45 for problems on data consistency. structions: Compare different consistency models (e.g., strong, eventual, causal) for distributed databases. Evaluate the trade-offs between availability and consistency in a given use case. Propose the most appropriate model for the scenario and explain your reasoning. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qoHazb9tC440AZF/view?usp=sharing]arrow_forwardOperating Systems: Deadlock Detection fer to page 25 for problems on deadlock concepts. structions: • Given a system resource allocation graph, determine if a deadlock exists. If a deadlock exists, identify the processes and resources involved. Suggest strategies to prevent or resolve the deadlock and explain their trade-offs. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qoHazb9tC440 AZF/view?usp=sharing]arrow_forwardArtificial Intelligence: Heuristic Evaluation fer to page 55 for problems on Al search algorithms. tructions: Given a search problem, propose and evaluate a heuristic function. Compare its performance to other heuristics based on search cost and solution quality. Justify why the chosen heuristic is admissible and/or consistent. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qoHazb9tC440 AZF/view?usp=sharing]arrow_forward
- Refer to page 75 for graph-related problems. Instructions: • Implement a greedy graph coloring algorithm for the given graph. • Demonstrate the steps to assign colors while minimizing the chromatic number. • Analyze the time complexity and limitations of the approach. Link [https://drive.google.com/file/d/1wKSrun-GlxirS3IZ9qoHazb9tC440 AZF/view?usp=sharing]arrow_forwardRefer to page 150 for problems on socket programming. Instructions: • Develop a client-server application using sockets to exchange messages. • Implement both TCP and UDP communication and highlight their differences. • Test the program under different network conditions and analyze results. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qo Hazb9tC440AZF/view?usp=sharing]arrow_forwardRefer to page 80 for problems on white-box testing. Instructions: • Perform control flow testing for the given program, drawing the control flow graph (CFG). • Design test cases to achieve statement, branch, and path coverage. • Justify the adequacy of your test cases using the CFG. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS3IZ9qo Hazb9tC440 AZF/view?usp=sharing]arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 C++ Programming: From Problem Analysis to Program...Computer ScienceISBN:9781337102087Author:D. S. MalikPublisher:Cengage Learning
C++ Programming: From Problem Analysis to Program...Computer ScienceISBN:9781337102087Author:D. S. MalikPublisher:Cengage Learning

C++ Programming: From Problem Analysis to Program...
Computer Science
ISBN:9781337102087
Author:D. S. Malik
Publisher:Cengage Learning