
Concept explainers
To find: the ratio of FOFI and HIIK from a given
Answer to Problem 2PS
FOFI=1729 and HIIK=89 .
Explanation of Solution
Given:
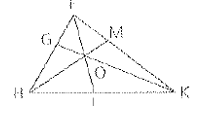
HGHF=49 andFMMK=23 .
Concept used:
If two points balanced the product of the mass and distance from the line of the balance of on point will be equal to the product if the mass and distance from the same line balance of the other point.
w1w2=l2l1.w1×l1=w2×l2.wb=w1+w2.
Where wb is weight at which the weight is divided or incase of triangle the line which bisect the two weight.
Calculation:
According to the given:
HGHF=49 andFMMK=23 .
From the ratio from given the line HG provides a weight on F or wF=4.
Similarly, the ratio from the given line FK provides a weight on F or wF=3.
Therefore, the weight on F
wF=3 or 4 so, take the multiple of both which is wF=12 .
wH=9.WK=8.
Which implies weight on I :
wI=17.
According to the given diagram:
FI=FO+OI.FI=17+12=29.FOFI=1729.
Similarly, that of ratio of
HIIK=89 .
Hence, FOFI=1729 and HIIK=89 .
Chapter 16 Solutions
Geometry For Enjoyment And Challenge
Additional Math Textbook Solutions
Introductory Statistics
University Calculus: Early Transcendentals (4th Edition)
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Calculus: Early Transcendentals (2nd Edition)
Elementary Statistics
Intro Stats, Books a la Carte Edition (5th Edition)
- Door 87.5in to 47 living 44.75 Closet 96in Window ISS.Sin 48in Train Table 96in 48in 132:2 Windowarrow_forward39 Two sides of one triangle are congruent to two sides of a second triangle, and the included angles are supplementary. The area of one triangle is 41. Can the area of the second triangle be found?arrow_forwardA parallelogram with an area of 211.41 m^2 hast a base Thatcher measures 24.3m. Find ist height.arrow_forward
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning

