Chapter 1.6, Problem 37PPS

a

To determine

To make a table showing the relation between body and water weight for people weighing 100, 105, 110,120,125 and 130 pounds.

Explanation of Solution

Given:

The given relation is $w=2(\frac{b}{3})$

Where w = weight of water in pounds.

b = body weight in pounds.

Calculation:

When the body weight ( b) =100 pounds, weight of water ( w ) is = $2(\frac{100}{3})=66.66$ pounds.

Similarly,

Values of ‘ b’	Values of ‘ w’
100	$2(\frac{100}{3})$ = 66.67
105	$2(\frac{105}{3})$ = 70
110	$2(\frac{110}{3})$ = 73.33
120	$2(\frac{120}{3})$ = 80
125	$2(\frac{125}{3})$ = 83.33
130	$2(\frac{130}{3})$ = 86.67

Conclusion:

The above table shows the relation between body and water weight for people.

b

To determine

To identify the dependent and independent variables from the given relation.

Answer to Problem 37PPS

Weight of body is independent variable.

Weight of water is dependent variable.

Explanation of Solution

Given:

The given relation is $w=2(\frac{b}{3})$

Independent variables are those variables which keeps on changing and they are unaffected by the change of any other parameter. For example: - Time.

Hence, Weight of the body ( b) is the deciding parameter which does not depend on other variable. So it is the independent variable.

Weight of the water ( w) depends on weight of the body ( b) as per the given relation.

So, the Weight of the water is the dependent variable.

Conclusion:

Therefore, weight of body is independent variable and weight of water is dependent variable.

c

To determine

To write: the domain and range of the relation $w=2(\frac{b}{3})$ and graph it

Answer to Problem 37PPS

Domain $\to (0,\infty )$

Range $\to (0,\infty )$

Explanation of Solution

Given:

The relation is $w=2(\frac{b}{3})$

Domain is all the values of x - axis that is defined in the given relation.

Range is all the values of y - axis that are possible for corresponding values of x - axis.

Hence, for the relation $w=2(\frac{b}{3})$ , the domain is: $b\in (0,\infty )$ and range is: $w\in (0,\infty )$

Calculation for graph:

Consider $w=2(\frac{b}{3})$

Values of ‘ b’	Values of ‘ w’
100	$2(\frac{100}{3})$ = 66.67
105	$2(\frac{105}{3})$ = 70
110	$2(\frac{110}{3})$ = 73.33
120	$2(\frac{120}{3})$ = 80
125	$2(\frac{125}{3})$ = 83.33
130	$2(\frac{130}{3})$ = 86.67

By taking different values of b , the graph can be plotted.

Graph:

  

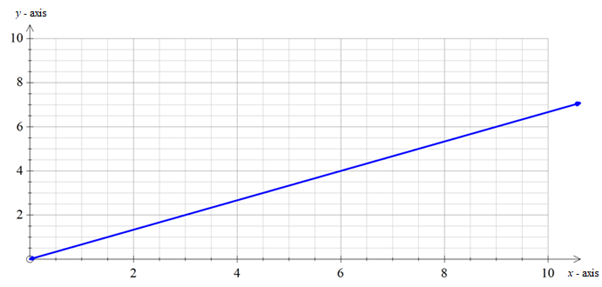
Interpretation:

From the above graph, it is clear that,

As the weight of the body increases, the weight of the water also increases.

d

To determine

To reverse the independent and dependent variable of the given relation, graph it and interpret the meaning of the graph.

Explanation of Solution

Given:

The relation is $w=2(\frac{b}{3})$

Here, Weight of the body ( b ) is the independent variable.

Weight of water ( w) is the dependent variable

The given relation after reversing the independent and dependent variable is $b=2(\frac{w}{3})$ .

This means, for every 3 pounds of water, there will be 2 pounds of body weight for an adult.

Calculation for graph:

Consider $w=2(\frac{b}{3})$

Values of ‘ w’	Values of ‘ b’
100	$2(\frac{100}{3})$ =66.67
105	$2(\frac{105}{3})$ =70
110	$2(\frac{110}{3})$ =73.33
120	$2(\frac{120}{3})$ =80
125	$2(\frac{125}{3})$ =83.33
130	$2(\frac{130}{3})$ =86.67

Graph:

  

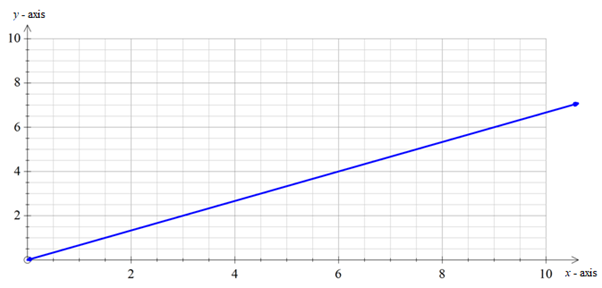
In the above graph, x - axis denotes the weight of the water ( w) in pounds.

y - axis denotes the weight of the body ( b ) in pounds.

Interpretation:

From the above graph, it is clear that,

As the weight of the water increases, the weight of the body also increases.