
Concept explainers
The flow
where
(a) Given the parameters n
(b) Repeat part (a), but include the cost of excavation. To do this minimize the following cost function,
where
(c) Discuss the implications of your results.
(a)
To calculate: The values of that will minimize the wetted perimeter P if the Manning equation of flow Q
can be written as
Answer to Problem 19P
Solution:
The values of
that will minimize the wetted perimeter P is
respectively.
Explanation of Solution
Given Information:
The Manning equation of flow Q
can be written as
where n is Manning roughness coefficient,
is cross-sectional are of channel
is given by
where P is wetted perimeter and it is defined by
where H is depth
and the parameters value are given as
Calculation:
Consider the equation,
The constrained can be written as,
This problem can be solved out by Linear programming formulation.
To minimize the wetted perimeter P function with the given constraint, the excel solver can be used.
The excel solver steps are,
Step 1. Initiate quantity
and then write the parameter as shown below,
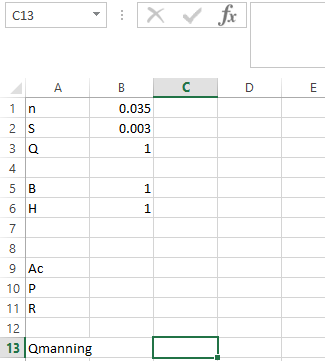
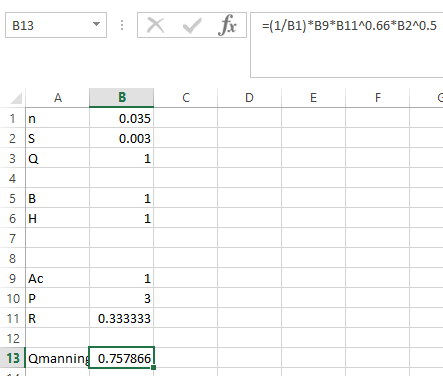
Step 2. Apply the formula in
as shown below,
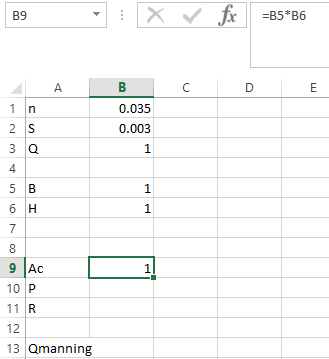
Step 3. Apply the formula in P as shown below,
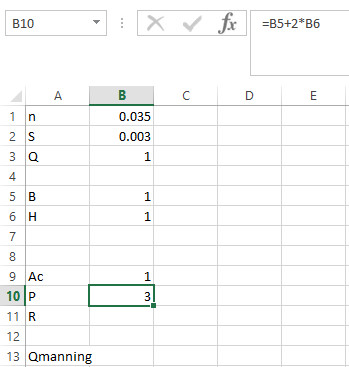
Step 4. Apply the formula in R as shown below,
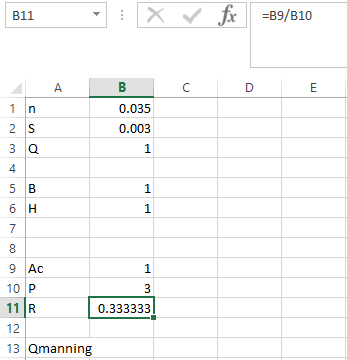
Step 5. Apply the formula in Qmanning as shown below,
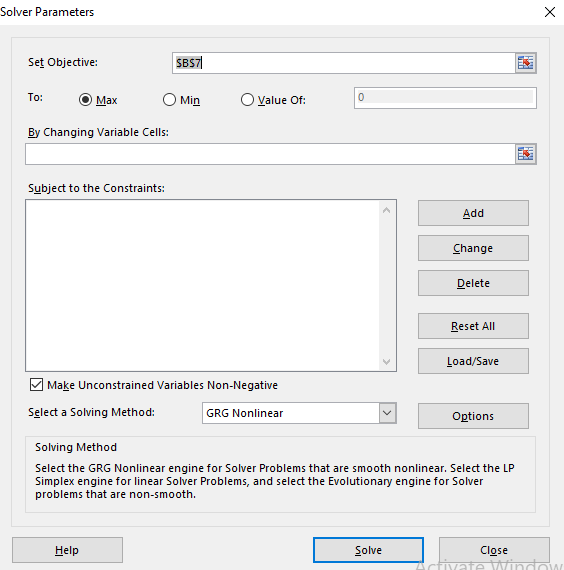
Step 6. Go to DATA and then click on Solver. This dialog box will appear.
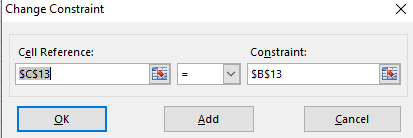
Step 7. Select the set objective, min, changing variable and then add,
Step 8. Click OK then this dialog box appears.
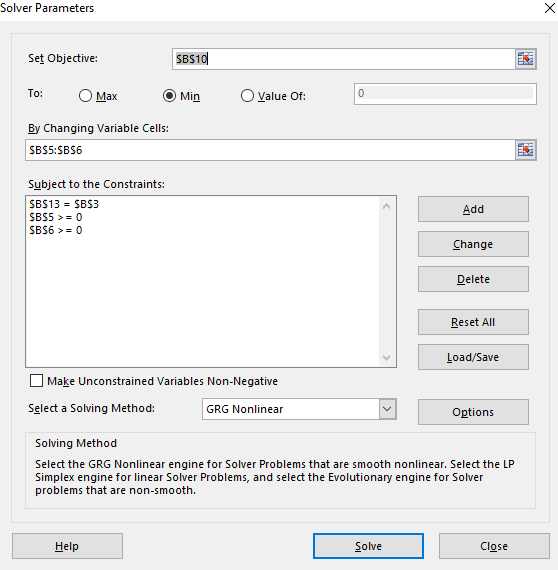
Step 9. Click on Solve and then OK.
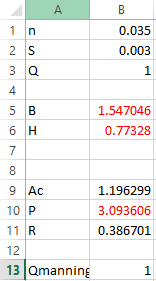
Hence, the values of
that will minimize the wetted perimeter P is
respectively.
(b)
To calculate: The values of
that will minimize the excavation cost function
is
and cost factor for lining
if the Manning equation of flow Q
can be written as
Answer to Problem 19P
Solution:
The values of
that will minimize the cost function P is
respectively.
Explanation of Solution
Given Information:
The Manning equation of flow Q
can be written as
where n is Manning roughness coefficient,
is cross-sectional are of channel
is given by
where P is wetted perimeter and it is defined by
where H is depth
and the parameters value are given as
Calculation:
Consider the function,
The constrained can be written as,
This problem can be solved out by Linear programming formulation.
To minimize the cost function with the given constraint, the excel solver can be used.
The excel solver steps are,
Step 1. Initiate quantity
and then write the parameter as shown below,

Step 2. Apply the formula in
as shown below,

Step 3. Apply the formula in P as shown below,

Step 4. Apply the formula in R as shown below,

Step 5. Apply the formula in Qmanning as shown below,

Step 6. Apply the formula in Cost as shown below,
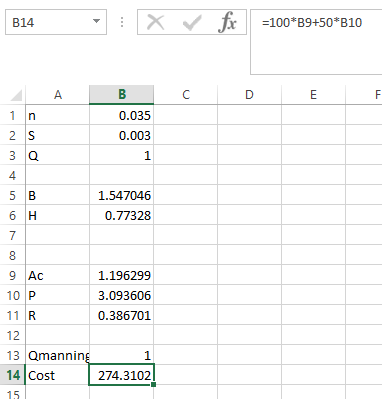
Step 7. Go to DATA and then click on Solver. This dialog box will appear.

Step 8. Select the set objective, min, changing variable and then add,

Step 9. Click OK then this dialog box appears.

Step 10. Click on Solve and then OK.
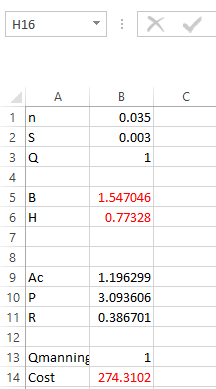
Hence, the values of
that will minimize the cost function is
respectively.
(c)
The implication of the result obtained in part (a) and part (b).
Answer to Problem 19P
Solution:
This can be interpreted that both the excavation and limiting cost can be minimized simultaneously by considering the bottom width B that is twice the length of each vertical side H.
Explanation of Solution
To interpret the result, first consider the constraint equation,
And,
On further simplification,
As
are dependent on B and H, thus both have minimized.
Thus, the excavation cost function
is minimized and as excavation cost C is directly proportional to cross-sectional area.
Hence, both the excavation and limiting cost can be minimized simultaneously by considering the bottom width B that is twice the length of each vertical side H as obtained in part (a) and (b) as
Want to see more full solutions like this?
Chapter 16 Solutions
Numerical Methods for Engineers
- In the system shown in the (img 1), water flows through the pump at a rate of 50L/s. The permissible NPSH providedby the manufacturer with that flow is 3.6 m. Determine the maximum height Delta z above the water surface at which the Pump can be installed to operate without cavitation. Include all losses in the suction tube. What is the value of the smaller total losses? What is the value of minor-minor losses? What is the value of major-minor losses?arrow_forwardA plastic canister whose bottom surface can be approximated as a flat surface1.9 m and 3 m long, travels through the water at 19 °C with a speed of up to 48 km/h. Determine: Drag due to friction that water exerts on the boat The power needed to overcome itarrow_forward(Fig. 1) shows the performance of a centrifugal pump for various diameters of theimpeller. For such a pump with a 5" diameter impeller, what power, in hp, would be expected to supply 5 L/s?what is its efficiency, in %?A pumping system requires 6 L/s of water with a load of 8 m, which of the pumpsof (fig. 1) would you recommend for this application?;arrow_forward
- You have the following information about a ship (image 1) Determine:a) Calculation of the block coefficient. b) Calculation of the wake coefficient. c) Determine the length of the wake.arrow_forwardA stainless steel canoe moves horizontally along the surface of a lake at 3.7 mi/h. TheThe lake's water temperature is 60°F. The bottom of the canoe is 25 ft long and flat. The boundary layer inThe bottom of the canoe is laminar or turbulent. the value of kinematic viscosity is? the value of the Reynolds number is?arrow_forwardExample Example 1 A vertical tubular test section is to be installed in an experimental high pressure water loop. The tube is 10.16 mm i.d. and 3.66 m long heated uniformly over its EXAMPLE 73 length. An estimate of the pressure drop across the test section is required as a function of the flow-rate of water entering the test section at 204°C and 68.9 bar. (1) Calculate the pressure drop over the test section for a water flow of 0.108 kg/s with a power of 100 kW applied to the tube using (i) the homogeneous model (ii) the Martinelli-Nelson model (iii) The Thom correlation (iv) the Baroczy correlation (2) Estimate the pressure drop versus flow-rate relationship over the range 0.108 to 0.811 kg/s (2-15 USGPM) for a power of 100 kW and 200 kW applied to the tube using (i) the Martinelli-Nelson model (ii) the Baroczy correlationarrow_forward
- "A seismograph detects vibrations caused by seismic movements. To model this system, it is assumed that the structure undergoes a vibration with a known amplitude band frequency w (rad/s), such that its vertical displacement is given by xB=bsin(wt). This movement of the structure will produce a relative acceleration in the mass m of 2 kg, whose displacement 2 will be plotted on a roller." x= 15 kN/m Structure -WI 24 mm (Ctrl) sin(wt) b(w/w)² √√1 (w/w)] + [25(w/w)]²' "The seismograph's roller measures 60 mm, and a maximum vibration amplitude of the structure of b<5 mm is expected. Design the damper (constant c) to ensure that, for a constant oscillation, the seismograph functions correctly and the needle does not move off the roller."arrow_forwardAircraft B is traveling at a steady speed of VB = 400 mi/hr at an altitude of 6000 ft. Meanwhile, when aircraft A is at an altitude of 10,000 ft, the line connecting A to B lies in the vertical plane of B's flight path and forms an angle of 0 = 30 degrees with the vertical. Assuming A maintains a constant velocity, find the speed required for a collision to occur. Additionally, calculate the time it would take for the collision to happen after both aircraft reach the described positions, provided no evasive measures are taken. Problem outline: 1- Find the velocity of A for the collision to happen. 2- Find the time at which the collision happens. 3- Explain the solution process with your own words. - 10,000 ft 12° 6000 ft B UBarrow_forwardDetermine the gross take-off weight of the aircraftarrow_forward
 Principles of Heat Transfer (Activate Learning wi...Mechanical EngineeringISBN:9781305387102Author:Kreith, Frank; Manglik, Raj M.Publisher:Cengage Learning
Principles of Heat Transfer (Activate Learning wi...Mechanical EngineeringISBN:9781305387102Author:Kreith, Frank; Manglik, Raj M.Publisher:Cengage Learning
