Calculus Early Transcendentals, Binder Ready Version
Calculus Early Transcendentals, Binder Ready Version
11th Edition
ISBN: 9781118883822
Author: Howard Anton, Irl C. Bivens, Stephen Davis
Publisher: WILEY
bartleby

Concept explainers

Differential Equations
Have you ever observed the movement of the satellites and rockets or how the planets go around the sun in their orbits? How will you determine their motion? Definitely they follow some scientific laws and these kinds of problems are framed as differentia…
bartleby

Videos

Textbook Question
Book Icon
Chapter 15.1, Problem 47ES

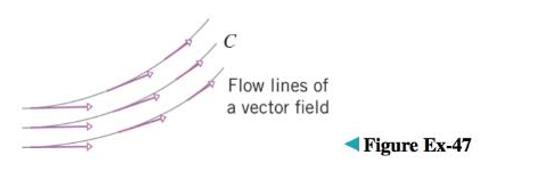
A curve C is called a flow line of a vector field F if F is a tangent vector to C at each point along C (See the accompanying figure).

(a) Let C be a flow line for F( x , y ) = − y i+ x j, and let ( x , y ) be a point on C for which y ≠ 0. Show that the flow lines satisfy the differential equation d y d x = − x y

(b) Solve the differential equation in part (a) by separation of variables, and show that the flow lines are concentric circles centered at the origin.

Chapter 15.1, Problem 47ES, A curve C is called a flow line of a vector field F if F is a tangent vector to C at each point

Expert Solution & Answer
Check Mark

Want to see the full answer?

Check out a sample textbook solution
Blurred answer
Previous
Chapter 15.1, Problem 46ES
Next
Chapter 15.1, Problem 48ES
Students have asked these similar questions
Since z = f( a, b, d, c), write the exact differential of the dependent variable.
(1n |t – 1], e', vî ) 1. Let 7(t) = (a) Express the vector valued function in parametric form. (b) Find the domain of the function. (c) Find the first derivative of the function. (d) Find T(2). (e) Find the vector equation of the tangent line to the curve when t=2. 2. Complete all parts: (a) Find the equation of the curve of intersection of the surfaces y = x? and z = x3 (b) What is the name of the resulting curve of intersection? (c) Find the equation for B the unit binormal vector to the curve when t= 1. Hint: Instead of using the usual formula for B note that the unit binormal vector is orthogonal to 7 '(t) and 7"(t). In fact, an alternate formula for this vector is ア'(t) × ア"(t) ア(t) ×デ"(t)| B(t) =

Chapter 15 Solutions

Calculus Early Transcendentals, Binder Ready Version

Ch. 15.1 - The function (x,y,z)=xy+yz+xz is a potential for...Ch. 15.1 - The vector field F(x,y,z)=, defined for...Ch. 15.1 - An inverse-square field is one that can be written...Ch. 15.1 - The vector field has divergence and curl Ch. 15.1 - Match the vector field F(x,y) with one of the...Ch. 15.1 - Match the vector field F(x,y) with one of the...Ch. 15.1 - Determine whether the statement about the vector...Ch. 15.1 - Determine whether the statement about the vector...Ch. 15.1 - Sketch the vector field by drawing some...Ch. 15.1 - Sketch the vector field by drawing some...
Ch. 15.1 - Sketch the vector field by drawing some...Ch. 15.1 - Sketch the vector field by drawing some...Ch. 15.1 - Use a graphing utility to generate a plot of the...Ch. 15.1 - Use a graphing utility to generate a plot of the...Ch. 15.1 - Determine whether the statement is true or false....Ch. 15.1 - Determine whether the statement is true or false....Ch. 15.1 - Determine whether the statement is true or false....Ch. 15.1 - Determine whether the statement is true or false....Ch. 15.1 - Confirm that is a potential function for F(r) on...Ch. 15.1 - Confirm that is a potential function for F(r) on...Ch. 15.1 - Find div F and curl F . F(x,y,z)=x2i2j+yzkCh. 15.1 - Find div F and curl F . F(x,y,z)=xz3i+2y4x2j+5z2ykCh. 15.1 - Find div and curl . Ch. 15.1 - Find div and curl . Ch. 15.1 - Find div F and curl F ....Ch. 15.1 - Find div F and curl F ....Ch. 15.1 - Find(FG).F(x,y,z)=2xi+j+4ykG(x,y,z)=xi+yjzkCh. 15.1 - Find(FG).F(x,y,z)=yzi+xzj+xykG(x,y,z)=xyj+xyzkCh. 15.1 - Find(F).F(x,y,z)=sinxi+cos(xy)j+zkCh. 15.1 - Find(F).F(x,y,z)=exzi+3xeyjeyzkCh. 15.1 - Find(F).F(x,y,z)=xyj+xyzkCh. 15.1 - Find(F).F(x,y,z)=y2xi3yzj+xykCh. 15.1 - Use a CAS to check the calculations in Exercises...Ch. 15.1 - Use a CAS to check the calculations in Exercises...Ch. 15.1 - Let k be a constant, F=F(x,y,z),G=G(x,y,z), and...Ch. 15.1 - Let k be a constant, F=F(x,y,z),G=G(x,y,z), and...Ch. 15.1 - Let k be a constant, F=F(x,y,z),G=G(x,y,z), and...Ch. 15.1 - Let k be a constant, F=F(x,y,z),G=G(x,y,z), and...Ch. 15.1 - Let k be a constant, F=F(x,y,z),G=G(x,y,z), and...Ch. 15.1 - Let k be a constant, F=F(x,y,z),G=G(x,y,z), and...Ch. 15.1 - Let k be a constant, F=F(x,y,z),G=G(x,y,z), and...Ch. 15.1 - Let k be a constant, F=F(x,y,z),G=G(x,y,z), and...Ch. 15.1 - Rewrite the identities in Exercises 31, 33, 35,...Ch. 15.1 - Rewrite the identities in Exercises 32, 34, 36,...Ch. 15.1 - Verify that the radius vector r=xi+yj+zk has the...Ch. 15.1 - Verify that the radius vector r=xi+yj+zk has the...Ch. 15.1 - Letr=xi+yj+zk,letr=r,letf be a differentiable...Ch. 15.1 - (a) Use part (a) of Exercise 43, Exercise 36, and...Ch. 15.1 - Use the result in Exercise 43(b) to show that the...Ch. 15.1 - Use the result of Exercise 43(b) to show that if F...Ch. 15.1 - A curve C is called a flow line of a vector field...Ch. 15.1 - Find a differential equation satisfied by the flow...Ch. 15.1 - Find a differential equation satisfied by the flow...Ch. 15.1 - Find a differential equation satisfied by the flow...Ch. 15.2 - The area of the surface extending upward from the...Ch. 15.2 - Suppose that a wire has equation y=1x(0x1) and...Ch. 15.2 - If C is the curve represented by the equations...Ch. 15.2 - Prob. 4QCECh. 15.2 - Let C be the line segment from (0.0)to(0,1). In...Ch. 15.2 - Let C be the line segment from (0,2)to(0,4). ln...Ch. 15.2 - Evaluate CFdr by inspection for the force field...Ch. 15.2 - Evaluate CFdr by inspection for the force field...Ch. 15.2 - Use (30) to explain why the line integral in part...Ch. 15.2 - (a) Use (30) to explain why the line integral in...Ch. 15.2 - Evaluate CFdr along the line segment C from PtoQ....Ch. 15.2 - Evaluate CFdr along the line segment C from PtoQ....Ch. 15.2 - Evaluate CFdr along the line segment C from PtoQ....Ch. 15.2 - Evaluate CFdr along the line segment C from PtoQ....Ch. 15.2 - Let C be the curve represented by the equations...Ch. 15.2 - Let C be the curve represented by the equations...Ch. 15.2 - In each part, evaluate the integral...Ch. 15.2 - In each part, evaluate the integral Cydx+zdyxdz...Ch. 15.2 - Prob. 15ESCh. 15.2 - Determine whether the statement is true or false....Ch. 15.2 - Determine whether the statement is true or false....Ch. 15.2 - If a smooth oriented curve C in the xy-plane is a...Ch. 15.2 - Evaluate the line integral with respect to s along...Ch. 15.2 - Evaluate the line integral with respect to s along...Ch. 15.2 - Evaluate the line integral with respect to s along...Ch. 15.2 - Evaluate the line integral with respect to s along...Ch. 15.2 - Evaluate the line integral along the curve C....Ch. 15.2 - Evaluate the line integral along the curve C....Ch. 15.2 - Evaluate the line integral along the curve C....Ch. 15.2 - Evaluate the line integral along the curve C....Ch. 15.2 - Evaluate the line integral along the curve C....Ch. 15.2 - Evaluate the line integral along the curve C....Ch. 15.2 - Evaluate the line integral along the curve C....Ch. 15.2 - Evaluate the line integral along the curve C....Ch. 15.2 - Use a CAS to evaluate the line integrals along the...Ch. 15.2 - Use a CAS to evaluate the line integrals along the...Ch. 15.2 - Evaluate Cydxxdy along the curve C shown in the...Ch. 15.2 - Evaluate Cydxxdy along the curve C shown in the...Ch. 15.2 - Evaluate Cx2zdxyx2dy+3dz along the curve C shown...Ch. 15.2 - Evaluate Cx2zdxyx2dy+3dz along the curve C shown...Ch. 15.2 - Evaluate CFdr along the curve C....Ch. 15.2 - Evaluate CFdr along the curves C....Ch. 15.2 - Evaluate CFdr along the curves C....Ch. 15.2 - Prob. 40ESCh. 15.2 - Find the mass of a thin wire shaped in the form of...Ch. 15.2 - Find the mass of a thin wire shaped in the form of...Ch. 15.2 - Find the mass of a thin wire shaped in the form of...Ch. 15.2 - Find the mass of a thin wire shaped in the form of...Ch. 15.2 - Find the work done by the force field F on a...Ch. 15.2 - Find the work done by the force F on a particle...Ch. 15.2 - Find the work done by the force field F on a...Ch. 15.2 - Find the work done by the force field F on a...Ch. 15.2 - Find the work done by the force field...Ch. 15.2 - Find the work done by the force field...Ch. 15.2 - Use a line integral to find the area of the...Ch. 15.2 - Use a line integral to find the area of the...Ch. 15.2 - As illustrated in the accompanying figure, a...Ch. 15.2 - Evaluate the integral Cxdyydxx2+y2, where C is the...Ch. 15.2 - Suppose that a particle moves through the force...Ch. 15.2 - A farmer weighting 150 lb carries a sack of gain...Ch. 15.2 - Suppose that a curve C in the xy-plane is smoothly...Ch. 15.3 - If C is a piecewise smooth curve from...Ch. 15.3 - Prob. 2QCECh. 15.3 - A potential function for the vector field...Ch. 15.3 - If a, b. and c are nonzero real numbers such that...Ch. 15.3 - Determine whether F is a conservative vector...Ch. 15.3 - Determine whether F is a conservative vector...Ch. 15.3 - Determine whether F is a conservative vector...Ch. 15.3 - Determine whether F is a conservative vector...Ch. 15.3 - Determine whether F is a conservative vector...Ch. 15.3 - Determine whether F is a conservative vector...Ch. 15.3 - In each part, evaluate C2xy3dx+1+3x2y2dy over the...Ch. 15.3 - Prob. 8ESCh. 15.3 - Show that the integral is independent of the path,...Ch. 15.3 - Show that the integral is independent of the path,...Ch. 15.3 - Show that the integral is independent of the path,...Ch. 15.3 - Show that the integral is independent of the path,...Ch. 15.3 - Show that the integral is independent of the path,...Ch. 15.3 - Show that the integral is independent of the path,...Ch. 15.3 - Confirm that the force field F is conservative in...Ch. 15.3 - Confirm that the force field F is conservative in...Ch. 15.3 - Confirm that the force field F is conservative in...Ch. 15.3 - Confirm that the force field F is conservative in...Ch. 15.3 - Determine whether the statement is true or false....Ch. 15.3 - Determine whether the statement is true or false....Ch. 15.3 - Determine whether the statement is true or false....Ch. 15.3 - Prob. 22ESCh. 15.3 - Find the exact value of CFdr using any method....Ch. 15.3 - Find the exact value of CFdr using any method....Ch. 15.3 - Use the numerical integration capability of a CAS...Ch. 15.3 - Use the numerical integration capability of a CAS...Ch. 15.3 - Is the vector field conservative? Explain.Ch. 15.3 - Is the vector field conservative? Explain.Ch. 15.3 - Prove: If Fx,y,z=fx,y,zi+gx,y,zj+hx,y,zk is a...Ch. 15.3 - Use the result in Exercise 31 to show that the...Ch. 15.3 - Find a nonzero function h for which...Ch. 15.3 - (a) In Example 3 of Section 15.1 we showed that...Ch. 15.3 - Use the result in Exercise 34(b). In each part,...Ch. 15.3 - Use the result in Exercise 34(b). Let...Ch. 15.3 - Prove Theorem 15.3.1 if C is a piecewise smooth...Ch. 15.3 - Prove that (b) implies (c) in Theorem 15.3.2.Ch. 15.3 - Complete the proof of Theorem 15.3.2 by showing...Ch. 15.4 - If C is the square with vertices 1,1 oriented...Ch. 15.4 - If C is the triangle with vertices 0,0,1,0,and1,1...Ch. 15.4 - Prob. 3QCECh. 15.4 - What region R and choice of functions fx,yandgx,y...Ch. 15.4 - Evaluate the line integral using Green’s Theorem...Ch. 15.4 - Prob. 2ESCh. 15.4 - Use Green’s Theorem to evaluate the integral. In...Ch. 15.4 - Use Green’s Theorem to evaluate the integral. In...Ch. 15.4 - Use Green’s Theorem to evaluate the integral. In...Ch. 15.4 - Use Green’s Theorem to evaluate the integral. In...Ch. 15.4 - Use Green’s Theorem to evaluate the integral. In...Ch. 15.4 - Use Green’s Theorem to evaluate the integral. In...Ch. 15.4 - Use Green’s Theorem to evaluate the integral. In...Ch. 15.4 - Use Green’s Theorem to evaluate the integral. In...Ch. 15.4 - Use Green’s Theorem to evaluate the integral. In...Ch. 15.4 - Use Green’s Theorem to evaluate the integral. In...Ch. 15.4 - Use Green’s Theorem to evaluate the integral. In...Ch. 15.4 - Let C be the boundary of the region enclosed...Ch. 15.4 - Determine whether the statement is true or false....Ch. 15.4 - Determine whether the statement is true or false....Ch. 15.4 - Determine whether the statement is true or false....Ch. 15.4 - Determine whether the statement is true or false....Ch. 15.4 - Use a CAS to check Green’s Theorem by evaluating...Ch. 15.4 - In Example 3, we used Green’s Theorem to obtain...Ch. 15.4 - Use a line integral to find the area of the region...Ch. 15.4 - Use a line integral to find the area of the...Ch. 15.4 - Use the formula A=12Cydx+xdy to find the area of...Ch. 15.4 - Use the formula A=12Cydx+xdy to find the area of...Ch. 15.4 - Suppose that Fx,y=fx,yi+gx,yj is a vector field...Ch. 15.4 - Suppose that Fx,y,=fx,yi+gx,yj is a vector field...Ch. 15.4 - Prob. 27ESCh. 15.4 - In the accompanying figure, C is a smooth oriented...Ch. 15.4 - Use Green’s Theorem to find the work done by the...Ch. 15.4 - Use Green’s Theorem to find the work done by the...Ch. 15.4 - Evaluate Cydxxdy, where C is cardioid r=a1+cos02Ch. 15.4 - Let R be a plane region with area A whose boundary...Ch. 15.4 - Use the result in Exercise 32 to find the centroid...Ch. 15.4 - Use the result in Exercise 32 to find the centroid...Ch. 15.4 - Use the result in Exercise 32 to find the centroid...Ch. 15.4 - Use the result in Exercise 32 to find the centroid...Ch. 15.4 - Find a simple closed curve C with counterclockwise...Ch. 15.4 - (a) Let C be the line segment from a point a,b to...Ch. 15.4 - Evaluate the integral CFdr, where C is the...Ch. 15.4 - Evaluate the integral CFdr, where C is the...Ch. 15.4 - Discuss the role of the Fundamental Theorem of...Ch. 15.5 - Consider the surface integral fx,y,zdS. (a) If is...Ch. 15.5 - If is the triangular region with vertices...Ch. 15.5 - If is the sphere of radius 2 centered at the...Ch. 15.5 - If fx,y,z is the mass density function of a curved...Ch. 15.5 - Evaluate the surface integral fx,y,zdS fx,y,z=x2;...Ch. 15.5 - Evaluate the surface integral fx,y,zdS fx,y,z=xy;...Ch. 15.5 - Evaluate the surface integral fx,y,zdS fx,y,z=x2y;...Ch. 15.5 - Evaluate the surface integral fx,y,zdS...Ch. 15.5 - Evaluate the surface integral fx,y,zdS fx,y,z=xyz;...Ch. 15.5 - Evaluate the surface integral fx,y,zdS fx,y,z=x+y;...Ch. 15.5 - Evaluate the surface integral fx,y,zdS...Ch. 15.5 - Evaluate the surface integral fx,y,zdS...Ch. 15.5 - Determine whether the statement is true or false....Ch. 15.5 - Determine whether the statement is true or false....Ch. 15.5 - Determine whether the statement is true or false....Ch. 15.5 - Determine whether the statement is true or false....Ch. 15.5 - Sometimes evaluating a surface integral results in...Ch. 15.5 - Sometimes evaluating a surface integral results in...Ch. 15.5 - In some cases it is possible to use Definition...Ch. 15.5 - In some cases it is possible to use Definition...Ch. 15.5 - In some cases it is possible to use Definition...Ch. 15.5 - Set up, but do not evaluate, an iterated integral...Ch. 15.5 - Set up, but do not evaluate, an iterated integral...Ch. 15.5 - Use a CAS to confirm that the three integrals you...Ch. 15.5 - Try to confirm with a CAS that the three integrals...Ch. 15.5 - Set up, but do not evaluate, two different...Ch. 15.5 - Set up, but do not evaluate, two different...Ch. 15.5 - Use a CAS to confirm that the two integrals you...Ch. 15.5 - Use a CAS to find the value of the surface...Ch. 15.5 - Find the mass of the lamina with constant density...Ch. 15.5 - Find the mass of the lamina with constant density...Ch. 15.5 - Find the mass of the lamina that is the portion of...Ch. 15.5 - Find the mass of the lamina that is the portion of...Ch. 15.5 - If a curved lamina has constant density 0, what...Ch. 15.5 - Show that if the density of the lamina x2+y2+z2=a2...Ch. 15.5 - The centroid of a surface is defined by...Ch. 15.5 - The centroid of a surface is defined by...Ch. 15.5 - Evaluate the integral fx,y,zdS over the surface ...Ch. 15.5 - Prob. 36ESCh. 15.5 - Prob. 37ESCh. 15.5 - Prob. 38ESCh. 15.5 - Use a CAS to approximate the mass of the curved...Ch. 15.5 - The surface shown in the accompanying figure on...Ch. 15.5 - Discuss the similarities and differences between...Ch. 15.6 - In these exercises, F(x,y,z) denotes a vector...Ch. 15.6 - In these exercises, F(x,y,z) denotes a vector...Ch. 15.6 - In these exercises, F(x,y,z) denotes a vector...Ch. 15.6 - In these exercises, F(x,y,z) denotes a vector...Ch. 15.6 - Suppose that the surface of the unit cube in the...Ch. 15.6 - Find the flux of the constant vector field...Ch. 15.6 - Find the flux of F(x,y,z)=xi through a square of...Ch. 15.6 - Find the flux of F(x,y,z)=(y+1)j through a square...Ch. 15.6 - Find the flux of Fx,y,z=xi+yj+z2+4k through a 23...Ch. 15.6 - Find the flux of F(x,y,z)=2i+3j through a disk of...Ch. 15.6 - Find the flux of F(x,y,z)=9j+8k through a disk of...Ch. 15.6 - Prob. 8ESCh. 15.6 - Find the flux of the vector field F across ....Ch. 15.6 - Find the flux of the vector field F across ....Ch. 15.6 - Find the flux of the vector field F across ....Ch. 15.6 - Find the flux of the vector field F across ....Ch. 15.6 - Find the flux of the vector field F across ....Ch. 15.6 - Find the flux of the vector field F across ....Ch. 15.6 - Find the flux of the vector field F across ....Ch. 15.6 - Find the flux of the vector field F across ....Ch. 15.6 - Find the flux of the vector field F across in the...Ch. 15.6 - Find the flux of the vector field F across in the...Ch. 15.6 - Find the flux of the vector field F across in the...Ch. 15.6 - Find the flux of the vector field F across in the...Ch. 15.6 - Let be the surface of the cube bounded by the...Ch. 15.6 - Let be the closed surface consisting of the...Ch. 15.6 - Determine whether the statement is true or false....Ch. 15.6 - Determine whether the statement is true or false....Ch. 15.6 - Determine whether the statement is true or false....Ch. 15.6 - Determine whether the statement is true or false....Ch. 15.6 - Find the flux of F across the surface by...Ch. 15.6 - Find the flux of F across the surface by...Ch. 15.6 - Let x,y,andz be measured in meters, and suppose...Ch. 15.6 - Let x,y,andz be measured in meters, and suppose...Ch. 15.6 - (a) Derive the analogs of Formulas (12) and (13)...Ch. 15.6 - (a) Derive the analogs of Formulas (12) and (13)...Ch. 15.6 - Let F=rkr,wherer=xi+yj+zkandkisaconstant. (Note...Ch. 15.6 - Let F(x,y,z)=a2xi+(y/a)j+az2k and let be the...Ch. 15.6 - Let F(x,y,z)=6a+1xi4ayj+a2zk and let be the...Ch. 15.6 - Discuss the similarities and differences between...Ch. 15.6 - Write a paragraph explaining the concept of flux...Ch. 15.7 - Let G be a solid whose surface is oriented outward...Ch. 15.7 - The outward flux of Fx,y,z=xi+yj+zk across any...Ch. 15.7 - If Fx,y,z is the velocity vector field for a...Ch. 15.7 - If F(r)=cr3r is an inverse-square field, and if ...Ch. 15.7 - Verify Formula (1) in the Divergence Theorem by...Ch. 15.7 - Verify Formula (1) in the Divergence Theorem by...Ch. 15.7 - Verify Formula (1) in the Divergence Theorem by...Ch. 15.7 - Verify Formula (1) in the Divergence Theorem by...Ch. 15.7 - Determine whether the statement is true or false....Ch. 15.7 - Determine whether the statement is true or false....Ch. 15.7 - Determine whether the statement is true or false....Ch. 15.7 - Determine whether the statement is true or false....Ch. 15.7 - Use the Divergence Theorem to find the flux of F...Ch. 15.7 - Use the Divergence Theorem to find the flux of F...Ch. 15.7 - Use the Divergence Theorem to find the flux of F...Ch. 15.7 - Use the Divergence Theorem to find the flux of F...Ch. 15.7 - Use the Divergence Theorem to find the flux of F...Ch. 15.7 - Use the Divergence Theorem to find the flux of F...Ch. 15.7 - Use the Divergence Theorem to find the flux of F...Ch. 15.7 - Use the Divergence Theorem to find the flux of F...Ch. 15.7 - Use the Divergence Theorem to find the flux of F...Ch. 15.7 - Use the Divergence Theorem to find the flux of F...Ch. 15.7 - Use the Divergence Theorem to find the flux of F...Ch. 15.7 - Prove that if r=xi+yj+zkand is the surface of a...Ch. 15.7 - Use the result in Exercise 20 to find the outward...Ch. 15.7 - Let Fx,y,z=ai+bj+ck be a constant vector field and...Ch. 15.7 - Find a vector field Fx,y,z that has (a) positive...Ch. 15.7 - Let Fx,y,z be a nonzero vector field in 3-space...Ch. 15.7 - Does the result in Exercise 25 remain true if the...Ch. 15.7 - Prove the identity, assuming that F, , and G...Ch. 15.7 - Prove the identity, assuming that F, , and G...Ch. 15.7 - Prove the identity, assuming that F, , and G...Ch. 15.7 - Prove the identity, assuming that F, , and G...Ch. 15.7 - Prove the identity, assuming that F, , and G...Ch. 15.7 - Use the Divergence Theorem to find all positive...Ch. 15.7 - Determine whether the vector field Fx,y,z is free...Ch. 15.7 - Determine whether the vector field Fx,y,z is free...Ch. 15.7 - Determine whether the vector field Fx,y,z is free...Ch. 15.7 - Determine whether the vector field Fx,y,z is free...Ch. 15.7 - Let be the surface of the solid G that is...Ch. 15.8 - Let be a piecewise smooth oriented surface that...Ch. 15.8 - We showed in Example 2 that the vector field...Ch. 15.8 - (a) If 1and2 are two oriented surface that have...Ch. 15.8 - For steady-state flow, the maximum circulation...Ch. 15.8 - Verify Formula (2) in stokes’ Theorem by...Ch. 15.8 - Verify Formula (2) in stokes’ Theorem by...Ch. 15.8 - Verify Formula (2) in stokes’ Theorem by...Ch. 15.8 - Verify Formula (2) in stokes’ Theorem by...Ch. 15.8 - Use Stokes’s Theorem to evaluate CF.dr....Ch. 15.8 - Use Stokes’s Theorem to evaluate CF.dr....Ch. 15.8 - Use Stokes’s Theorem to evaluate CF.dr....Ch. 15.8 - Use Stokes’s Theorem to evaluate CF.dr....Ch. 15.8 - Use Stokes’s Theorem to evaluate CF.dr....Ch. 15.8 - Use Stokes’s Theorem to evaluate CF.dr....Ch. 15.8 - Use Stokes’s Theorem to evaluate CF.dr....Ch. 15.8 - Use Stokes’s Theorem to evaluate CF.dr....Ch. 15.8 - Determine whether the statement is true or false....Ch. 15.8 - Determine whether the statement is true or false....Ch. 15.8 - Determine whether the statement is true or false....Ch. 15.8 - Determine whether the statement is true or false....Ch. 15.8 - Consider the vector field given by the formula...Ch. 15.8 - (a) Let denote the surface of a solid G with n...Ch. 15.8 - The figures in these exercises show a horizontal...Ch. 15.8 - The figures in these exercises show a horizontal...Ch. 15.8 - Let F(x,y,z) be a conservation vector field in...Ch. 15.8 - In 1831 the physicist Michael Faraday discovered...Ch. 15.8 - Let be the portion of the paraboloid z=1x2y2 for...Ch. 15.8 - Discuss what it mean to say that the curl of a...Ch. 15.8 - Compare and contrast the Fundamental Theorem of...Ch. 15 - In words, what is a vector field? Give some...Ch. 15 - (a) Give a physical example of an inverse-square...Ch. 15 - Find an explicit coordinate expression for the...Ch. 15 - Find x+yxy.Ch. 15 - Find curl zi+xj+yk.Ch. 15 - Let Fx,y,z=xx2+y2i+yx2+y2j+zx2+y2k Sketch the...Ch. 15 - Assume that C is the parametric curve x=xt,y=yt,...Ch. 15 - (a) Express the mass M of a thin wire in 3-space...Ch. 15 - Give a physical interpretation of CFTds.Ch. 15 - State some alternative notations for CFTds.Ch. 15 - Evaluate the line integral. Cxyds;C:x2+y2=1Ch. 15 - Evaluate the line integral....Ch. 15 - Evaluate the line integral....Ch. 15 - Find the work done by the force field Fx,y=y2i+xyj...Ch. 15 - State the Fundamental Theorem of Line Integrals,...Ch. 15 - Evaluate Cfdr where fx,y,z=xy2z3 and...Ch. 15 - Let Fx,y=yi2xj. (a) Find a nonzero function hx...Ch. 15 - Let Fx,y=yexy1i+xexyj. (a) Show that F is a...Ch. 15 - State Green's Theorem, including all of the...Ch. 15 - Express the area of a plane region as a line...Ch. 15 - Let and denote angles that satisfy 02 and assume...Ch. 15 - (a) Use Green's Theorem to prove that Cfxdx+gydy=0...Ch. 15 - Assume that is the parametric surface...Ch. 15 - Evaluate zdS;:x2+y2=10z1.Ch. 15 - Do you think that the surface in the accompanying...Ch. 15 - Give a physical interpretation of FndS.Ch. 15 - Find the flux of Fx,y,z=xi+yj+2zk through the...Ch. 15 - Find the flux of Fx,y,z=xi+2yj+3zk through the...Ch. 15 - State the Divergence Theorem and Stokes' Theorem,...Ch. 15 - Let G be a solid with the surface oriented by...Ch. 15 - Let be the sphere x2+y2+z2=1, let n be an inward...Ch. 15 - Use Stokes' Theorem to evaluate curlFndS where...Ch. 15 - Prob. 33RECh. 15 - With the aid of Exercise 33, determine whether F...Ch. 15 - With the aid of Exercise 33, determine whether F...Ch. 15 - As discussed in Example 1 of Section 15.1,...

Additional Math Textbook Solutions

Find more solutions based on key concepts
In Problems 51-66, find the domain of each function. h( x )= 3x-12

Precalculus

Find how many SDs above the mean price would be predicted to cost.

Intro Stats, Books a la Carte Edition (5th Edition)

A Bloomberg Businessweek subscriber study asked, In the past 12 months, when travelling for business, what type...

STATISTICS F/BUSINESS+ECONOMICS-TEXT

Fill in each blank so that the resulting statement is true. An equation that expresses a relationship between t...

Algebra and Trigonometry (6th Edition)

Finding the Margin of Error In Exercises 33 and 34, use the confidence interval to find the estimated margin of...

Elementary Statistics: Picturing the World (7th Edition)

Derivatives of Logarithms In Exercises 11–40, find the derivative of y with respect to x, t, or θ, as appropria...

University Calculus: Early Transcendentals (4th Edition)

Knowledge Booster
Background pattern image
Calculus
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.
Similar questions
Recommended textbooks for you
Text book image
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Text book image
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
SEE MORE TEXTBOOKS
01 - What Is A Differential Equation in Calculus? Learn to Solve Ordinary Differential Equations.; Author: Math and Science;https://www.youtube.com/watch?v=K80YEHQpx9g;License: Standard YouTube License, CC-BY
Higher Order Differential Equation with constant coefficient (GATE) (Part 1) l GATE 2018; Author: GATE Lectures by Dishank;https://www.youtube.com/watch?v=ODxP7BbqAjA;License: Standard YouTube License, CC-BY
Solution of Differential Equations and Initial Value Problems; Author: Jefril Amboy;https://www.youtube.com/watch?v=Q68sk7XS-dc;License: Standard YouTube License, CC-BY