Chapter 1.5, Problem 25AYU

To determine

To find:

1. The centre $\left(h,k\right)$ and radius of the circle $2\left(x-3\right)²+2y²=8$

2. The graph of the circle

3. Intercepts of the circle, if any

Answer to Problem 25AYU

$\text{Centre }\left(3,0\right);\text{ radius }=2;$

$x\text{-intercepts }=5,1;\text{ no }y\text{-intercept}$

Explanation of Solution

Given:

Equation of the circle $2\left(x-3\right)²+2y²=8$

Calculation:-

$2\left(x-3\right)²+2y²=8$

$\left(x-3\right)²+y²=4$   Divide both sides by 2

Let us write the equation of the circle in standard form $\left(x-3\right)²+(y-0)²=\left(2\right)²$.

Compare this equation with the equation $\left(x-h\right)²+(y-k)²=\left(r\right)²$.

The comparison yields the information about the circle. We see that $h=3,k=0$ and $r=2$.

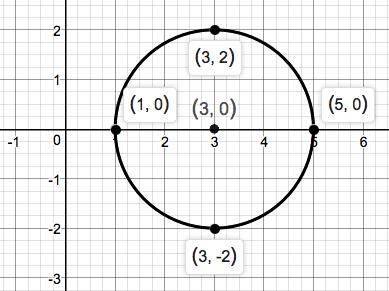
The circle has centre $\left(3,0\right)$ and a radius 2 units. To graph the circle, first plot the centre $\left(3,0\right)$. Since the radius is 2 units, locate four points on the circle by plotting 2 units to the left, to the right, up and down from the centre. These four points can be used to sketch the graph.

To find the $x\text{-intercepts}$, if any, let $y=0$ and solve for $x$.

$\left(x-3\right)²+(0-0)²=4$

$\left(x-3\right)²=4$

$x-3=\pm 2$   Subtract 1 from both sides

$\text{If,} x-3=2$

$x=5$

$\text{If,} x-3=\text{ −}2$

$x-3+3=\text{ −}2+3$

$x=1$

$x\text{-intercepts}$ are 5 and 1.

To find the $y\text{-intercepts}$, if any, let $x=0$ and solve for $y$.

$\left(0-3\right)²+\left(y-0\right)²=4$

$9+y²=4$

$9+y²-9=4-9$   Subtract 9 from both sides

$y²=-5$

This shows $y$ has no real value. Hence there is no $y\text{-intercept}$.