
Concept explainers
Consider the boundary-value problem
Approximate the solution of the differential equation at the interior points of the region with mesh size h =
The approximate solution of the given differential equation
Answer to Problem 1RE
The approximate solution of the differential equation at the interior points of the region is
Explanation of Solution
Formula used:
Calculation:
Consider the given boundary value problem.
For constructing a mesh with size with
Since
Similarly,
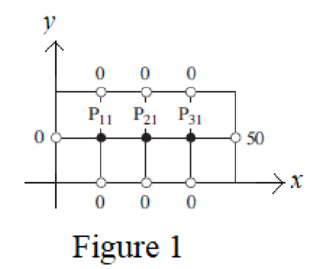
For
From the given boundary conditions
Repeat this for
Since there are less number of unknowns, use Gauss-elimination method to solve the system of equations.
Here, use row column transformations to obtain the values of
Further reduce the matrix as follows.
Therefore, the approximate solution of the differential equation at the interior points of the region is
Want to see more full solutions like this?
Chapter 15 Solutions
Differential Equations with Boundary-Value Problems (MindTap Course List)
- If x and y are elements of an ordered integral domain D, prove the following inequalities. a. x22xy+y20 b. x2+y2xy c. x2+y2xyarrow_forwardII. Given Fxy2) = (z2,xy, yz) and C is a triangle in the plane x + y +z = 2 with vertices (1,1,0), (1,0,1) & (0, 1, 1), use Stoke's Theorem to evaluate f F · dRarrow_forward3) Evaluate elz+y)/(z-y) dA where Ris the quadrilateral with vertices (0,1), (0,-2), (1,0), and (2,0) using the R change of variables where u = x + y and v = x – y. Give an exact solution (not a decimal approximation).arrow_forward
- Q.1. The set of all positive real numbers with the operations x + y = xy kx = xk Is it a vector space? Justify your answer.arrow_forward4. Write y as the sum of two orthogonal vectors, y, in L and in L Let y = YL = and u = 2 Let I be the line spanned by u. YL+ = ⠀arrow_forward2. 1 show thet vectors cre linecrly dependent or lineerly in dependontarrow_forward
- Prove that the pair of straight lines joining the origin to the points of inersection of the circles x² + y² = a² and x² + y² + 2(gx + fy) = 0 is a² (x² + y²) - 4(gx+fy)² = 0.arrow_forwardlet l={(x,y) 7x+4y=1} be a line in Cartesian model for Euclidean geometry. find a coordinate function (dont need to prove it)arrow_forwardCompute the intersections of the curve xy = 1 and the lines x +y = 5/2, x+y = 2, x+y = 0, x=0 , x=1 in the affine space and then in the projective space by using homogeneous coordinates. Complex solutions are valid. Please show your steps for both affine space and in project space. Box your final answer.arrow_forward
 Elements Of Modern AlgebraAlgebraISBN:9781285463230Author:Gilbert, Linda, JimmiePublisher:Cengage Learning,
Elements Of Modern AlgebraAlgebraISBN:9781285463230Author:Gilbert, Linda, JimmiePublisher:Cengage Learning,
