Chapter 15, Problem 1P

(a)

Program Plan Intro

To describe a dynamic-programming approach for finding longest simple path in directed acyclic graph and also give the running time of the algorithm.

Explanation of Solution

Given Information:

The shortest closed tour of the graph with length approximately is 24.89. The directed acyclic graph is shown below-

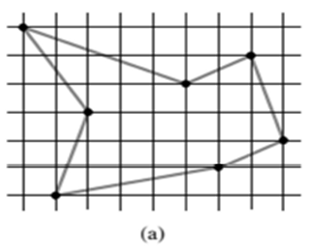
Explanation:

The dynamic-approach used to find the longest length simple path consider the graph G and vertices as V. The longest simple path must go through some edge of weight s or t . The algorithms to compute the longest weight path is $longest(G,s,t)=1+\max (longest(G,s\text{'},t))$ .

The base condition for the algorithm is $s=t$ and the initial length is 0.It can see that it consider this many possible sub-problems by taking |G| and complete graph on vertices V .

The algorithm to compute longest simple path in a directed acyclic graph is given below-

LONG-PATH(G,u,s,t,len)

If $t==s$ then

set $len(s)=0$ .

return ( len,u )

else if $u[s]==NULL$ then

Return (len,u).

else

for each adjacent vertex $u\in G$ of s.

Check the distance after adding new vertex i.

if $w(s,u)+len[u]\ge len[s]$ then

  $len[s]=w(s,u)+len[u]$ .

  $u[s]=t$ .

end if.

end for.

end if.

return ( len,u ).

end.

In above algorithm, loop of for is used to determine the longest path and the longest path visit all vertex by checking all adjacent vertex.

The time taken by the algorithm is depends upon the number of vertex visited and the number of edges in the longest simple path. Suppose V represent the number of vertex used in the computing the longest simple path and E represent the number of edges then total running time of the algorithm is equals to $O(V+E)$ .

(b)

Program Plan Intro

To describe a dynamic-programming approach for finding longest simple path in directed acyclic graph and also give the running time of the algorithm.

Explanation of Solution

Given Information:

The shortest closed tour of the graph with length approximately is 25.58. The directed acyclic graph is shown below-

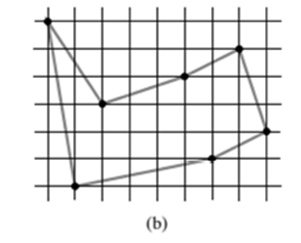
Explanation:

The longest simple path must go through some edge of weight s . The base condition for the algorithm is $s=t$ and the initial length is 0.It can see that it consider this many possible sub-problems by taking |G| and complete graph on vertices V .

The algorithm to compute longest simple path in a directed acyclic graph is given below-

LONG-PATH(G,u,s,t,len)

If $t==s$ then

set $len(s)=0$ .

return ( len,u )

else if $u[s]==NULL$ then

Return (len,u).

else

for each adjacent vertex $u\in G$ of s.

Check the distance after adding new vertex i.

if $w(s,u)+len[u]\ge len[s]$ then

  $len[s]=w(s,u)+len[u]$ .

  $u[s]=t$ .

end if.

end for.

end if.

return ( len,u ).

end.

The time taken by the algorithm is depends upon the number of vertex visited and the number of edges in the longest simple path. Suppose V represent the number of vertex used in the computing the longest simple path and E represent the number of edges then total running time of the algorithm is equals to $O(V+E)$ .

The above algorithm taken consideration of the nodes and generates the output according to the number of nodes in the graph so the longest length is computed by $longest(G,s,t)=1+\max (longest(G,s\text{'},t))$ .