Chapter 15, Problem 15A.3P

Interpretation Introduction

Interpretation:

The volume of a hexagonal unit cell has to be derived.

Concept Introduction:

From a vector analysis, we know that volume of a geometric system can be alternatively written as

  $V=\overrightarrow{a}.\overrightarrow{b}\times \overrightarrow{c}$

Explanation of Solution

First we have to derive the volume of a triclinic unit cell.  Then we can take it as the reference to derive the volume of a hexagonal unit cell.

Derivation of the volume of a triclinic unit cell:

The cell dimensions of a triclinic unit cell is $a\ne b\ne cand\alpha =\beta =\gamma ={90}^{\circ }$.

There are many choices for the primitive vectors in the triclinic system. So we are taking

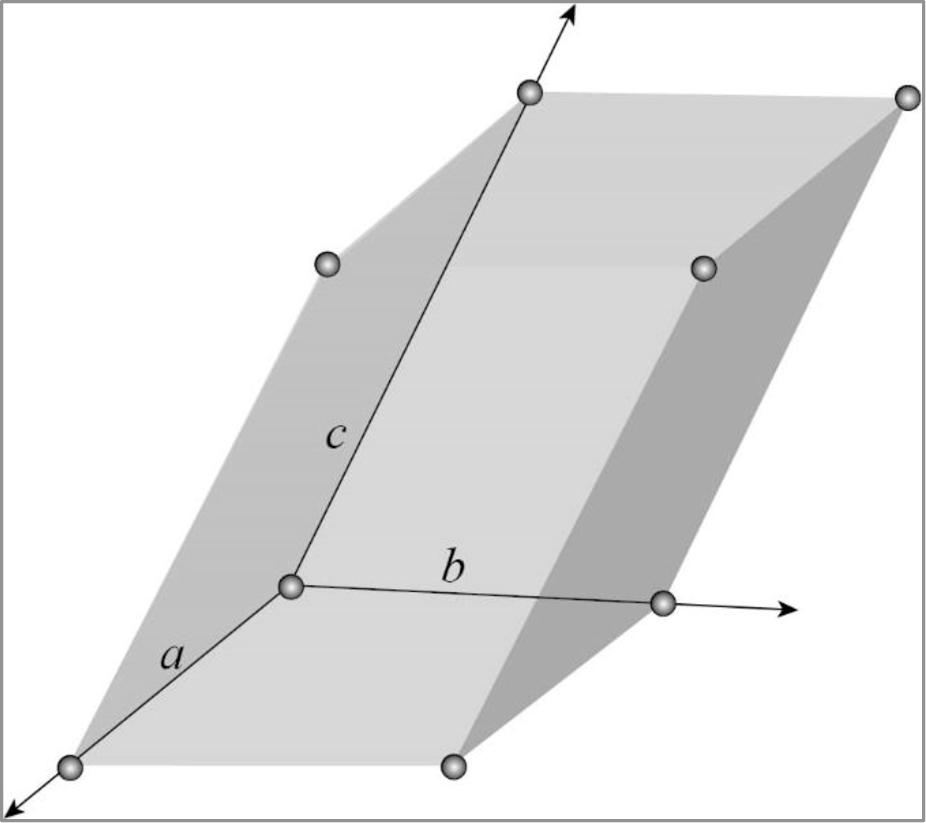
Figure.1

  $\begin{array}{l}a=a_x\widehat{i}+a_y\widehat{j}+a_z\widehat{k}\\ \\ b=b_x\widehat{i}+b_y\widehat{j}+b_z\widehat{k}\\ \\ c=c_x\widehat{i}+c_y\widehat{j}+c_z\widehat{k}\end{array}$

Then,

  $V=a.b\times c=\begin{array}{ccc}{a}_x& a_y& a_z\\ b_x& b_y& b_z\\ c_x& c_y& c_z\end{array}$

Therefore,

  $\begin{array}{c}{V}^2=\begin{array}{ccc}{a}_x& a_y& a_z\\ b_x& b_y& b_z\\ c_x& c_y& c_z\end{array}\begin{array}{ccc}{a}_x& a_y& a_z\\ b_x& b_y& b_z\\ c_x& c_y& c_z\end{array}\\ \\ =\begin{array}{ccc}{a}_x& a_y& a_z\\ b_x& b_y& b_z\\ c_x& c_y& c_z\end{array}\begin{array}{ccc}{a}_x& b_x& c_x\\ a_y& b_y& c_y\\ a_z& b_z& c_z\end{array}\left[Interchangerowsandcolumns\right]\\ \\ =\begin{array}{ccc}{a}_x{a}_x+a_y{a}_y+a_z{a}_z& a_x{b}_x+a_y{b}_y+a_z{b}_z& a_x{c}_x+a_y{c}_y+a_z{c}_z\\ b_x{a}_x+b_y{a}_y+b_z{a}_z& b_x{b}_x+b_y{b}_y+b_z{b}_z& b_x{c}_x+b_y{c}_y+b_z{c}_z\\ c_x{a}_x+c_y{a}_y+c_z{a}_z& c_x{b}_x+c_y{b}_y+c_z{b}_z& c_x{c}_x+c_y{c}_y+c_z{c}_z\end{array}\\ \\ =\begin{array}{ccc}{a}^2& a.b& a.c\\ b.a& b^2& b.c\\ c.a& c.b& c^2\end{array}=\begin{array}{ccc}{a}^2& ab\cos \gamma & ac\cos \beta \\ ab\cos \gamma & b^2& bc\cos \alpha \\ ac\cos \beta & bc\cos \alpha & c^2\end{array}\\ \\ =a^2{b}^2{c}^2\left(1-{\cos }^2\alpha -{\cos }^2\beta -{\cos }^2\gamma +2\cos \alpha \cos \beta \cos \gamma \right)\\ \\ Hence,V=abc{\left(1-{\cos }^2\alpha -{\cos }^2\beta -{\cos }^2\gamma +2\cos \alpha \cos \beta \cos \gamma \right)}^{1/2}\end{array}$

This is the expression for the volume of a triclinic unit cell.

Derivation of the volume of a hexagonal unit cell:

The cell dimensions of a hexagonal unit cell is $a=b\ne cand\alpha =\beta ={90}^{\circ },\gamma ={120}^{\circ }$.

Now substituting these values in the expression of the volume of a triclinic unit cell, we can get the exact expression for the hexagonal unit cell.

  $\begin{array}{c}V=abc{\left(1-{\cos }^2\alpha -{\cos }^2\beta -{\cos }^2\gamma +2\cos \alpha \cos \beta \cos \gamma \right)}^{1/2}\\ \\ =a.a.c{\left[1-{\cos }^2\left({90}^{\circ }\right)-{\cos }^2\left({90}^{\circ }\right)-{\cos }^2\left({120}^{\circ }\right)+2\cos \left({90}^{\circ }\right)\cos \left({90}^{\circ }\right)\cos \left({120}^{\circ }\right)\right]}^{1/2}\\ \\ =a^{2}c{\left[1-{\cos }^2\left({120}^{\circ }\right)\right]}^{1/2}=a^{2}c\sin \left({120}^{\circ }\right)=a^{2}c\sin \left({60}^{\circ }\right).\left[\begin{array}{l}\because \cos \left({90}^{\circ }\right)=0\\ 1-{\cos }^2\beta ={\sin }^2\beta \end{array}\right]\end{array}$

The above expression is for the volume of a hexagonal unit cell.