A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
13th Edition
ISBN: 9780135183885
Author: Rick Billstein, Shlomo Libeskind, Johnny Lott, Barbara Boschmans
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 14.1, Problem 11MC
The following figure is a partial tessellation of the plane with the trapezoid
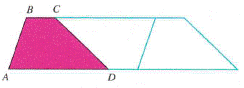
a. Tessellate the plane with a triangle and show how the tessellation can be used to find the relationship between the length of the segment connecting the midpoints of the two sides of a triangle and the length of the third side(the Midsegment Theorem of Chapter 12).
b. Explain how the tessellation can be used to find a relationship between the midsegment of the trapezoid and the bases.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
9. (a) Use pseudocode to describe an algo-
rithm for determining the value of a
game tree when both players follow a
minmax strategy.
(b) Suppose that T₁ and T2 are spanning
trees of a simple graph G. Moreover,
suppose that ₁ is an edge in T₁ that is
not in T2. Show that there is an edge
2 in T2 that is not in T₁ such that
T₁ remains a spanning tree if ₁ is
removed from it and 2 is added to it,
and T2 remains a spanning tree if 2 is
removed from it and e₁ is added to it.
(c) Show that a
degree-constrained
spanning tree of a simple graph in
which each vertex has degree not
exceeding 2 2 consists of a single
Hamiltonian path in the graph.
Chatgpt give wrong answer
No chatgpt pls will upvote
@when ever one Point sets in x are
closed a collection of functions which
separates Points from closed set
will separates Point.
18 (prod) is product topological
space then VaeA (xx, Tx) is homeomorphic
to sul space of the Product space
(Txa, prod).
KeA
© The Bin Projection map
B: Tx XP is continuous and open
but heed hot to be closed.
A collection (SEA) of continuos function
oha topolgical Space X se partes Points
from closed sets inx iff the set (v)
for KEA and Vopen set in Xx
from a base for top on x.
Chapter 14 Solutions
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Ch. 14.1 - Prob. 1MCCh. 14.1 - Prob. 3MCCh. 14.1 - Prob. 5MCCh. 14.1 - Prob. 6MCCh. 14.1 - Prob. 7MCCh. 14.1 - A drawing of a cube, shown in the following...Ch. 14.1 - Wall stenciling has been used to obtain an effect...Ch. 14.1 - Prob. 10MCCh. 14.1 - The following figure is a partial tessellation of...Ch. 14.1 - Prob. 12MC
Ch. 14.1 - Prob. 13MCCh. 14.1 - Prob. 14MCCh. 14.1 - Prob. 15MCCh. 14.1 - Prob. 18MCCh. 14.1 - Prob. 19MCCh. 14.1 - Prob. 20MCCh. 14.1 - Prob. 21MCCh. 14.1 - Karrin claims that centers of rotation must be at...Ch. 14.1 - A student asks if the image seen through a...Ch. 14.1 - Jillian wants to know why a regular pentagon will...Ch. 14.1 - Prob. 26MCCh. 14.1 - Prob. 1NAEPCh. 14.1 - Prob. 2NAEPCh. 14.1 - Prob. 3NAEPCh. 14.1A - For each of the following, find the image of the...Ch. 14.1A - Prob. 2ACh. 14.1A - Find the coordinates of the image for each of the...Ch. 14.1A - Prob. 4ACh. 14.1A - Prob. 7ACh. 14.1A - Prob. 8ACh. 14.1A - Prob. 9ACh. 14.1A - Prob. 11ACh. 14.1A - Prob. 12ACh. 14.1A - Prob. 13ACh. 14.1A - Prob. 14ACh. 14.1A - Prob. 15ACh. 14.1A - A 1-inch blue square piece of sidewalk chalk is...Ch. 14.1A - Prob. 17ACh. 14.1A - Prob. 18ACh. 14.1A - Prob. 19ACh. 14.1A - Prob. 20ACh. 14.1A - Prob. 22ACh. 14.1A - Prob. 23ACh. 14.1A - Prob. 24ACh. 14.1A - Prob. 25ACh. 14.1A - Prob. 26ACh. 14.1A - Prob. 27ACh. 14.1A - Prob. 28ACh. 14.1B - Prob. 2ACh. 14.1B - Prob. 3ACh. 14.1B - Prob. 4ACh. 14.1B - Prob. 7ACh. 14.1B - Prob. 11ACh. 14.1B - Prob. 12ACh. 14.1B - Prob. 13ACh. 14.1B - Prob. 14ACh. 14.1B - Prob. 15ACh. 14.2 - Prob. 1MCCh. 14.2 - Prob. 2MCCh. 14.2 - Prob. 3MCCh. 14.2 - Prob. 4MCCh. 14.2 - Prob. 5MCCh. 14.2 - Prob. 6MCCh. 14.2 - Prob. 7MCCh. 14.2 - Prob. 8MCCh. 14.2 - Prob. 9MCCh. 14.2 - Prob. 13MCCh. 14.2 - Prob. 15MCCh. 14.2 - Prob. 17MCCh. 14.2 - Prob. 18MCCh. 14.2 - Prob. 19MCCh. 14.2 - Prob. 20MCCh. 14.2 - Prob. 22MCCh. 14.2 - Prob. 1NAEPCh. 14.2 - Prob. 2NAEPCh. 14.2 - Prob. 3NAEPCh. 14.2 - Prob. 4NAEPCh. 14.2 - Prob. 5NAEPCh. 14.2A - Assessment 14-2A Describe how to find the image of...Ch. 14.2A - Prob. 2ACh. 14.2A - Assessment 14-2A Determine the final result when...Ch. 14.2A - Prob. 4ACh. 14.2A - Assessment 14-2A a. Refer to the following figure...Ch. 14.2A - Prob. 6ACh. 14.2A - a. Reflect triangle ABC across line j, then across...Ch. 14.2A - Assessment 14-2A Given ABC and its reflection...Ch. 14.2A - Prob. 9ACh. 14.2A - Prob. 10ACh. 14.2A - Decide whether a reflection, a translation, a...Ch. 14.2A - a. Conjecture what the image of a point with...Ch. 14.2A - Prob. 16ACh. 14.2A - Prob. 17ACh. 14.2A - Prob. 18ACh. 14.2A - Point P is the image of P not shown under a glide...Ch. 14.2A - Consider the glide reflection determined by the...Ch. 14.2B - Prob. 1ACh. 14.2B - Prob. 2ACh. 14.2B - Determine the final result when ABCis reflection...Ch. 14.2B - Prob. 4ACh. 14.2B - Prob. 6ACh. 14.2B - Prob. 7ACh. 14.2B - Prob. 8ACh. 14.2B - Prob. 9ACh. 14.2B - Prob. 10ACh. 14.2B - Prob. 11ACh. 14.2B - Prob. 12ACh. 14.2B - Prob. 13ACh. 14.2B - Prob. 14ACh. 14.2B - Prob. 15ACh. 14.2B - In which line will the two intersecting circles...Ch. 14.2B - Prob. 18ACh. 14.2B - If PQ is the image PQ not shown under a glide...Ch. 14.2B - Prob. 20ACh. 14.2B - Prob. 21ACh. 14.3 - Prob. 1MCCh. 14.3 - Prob. 2MCCh. 14.3 - Prob. 3MCCh. 14.3 - Prob. 5MCCh. 14.3 - Prob. 6MCCh. 14.3 - Prob. 7MCCh. 14.3 - Prob. 8MCCh. 14.3 - Prob. 9MCCh. 14.3 - Prob. 10MCCh. 14.3 - Prob. 12MCCh. 14.3 - Prob. 13MCCh. 14.3 - Prob. 14MCCh. 14.3 - Prob. 15MCCh. 14.3 - Prob. 16MCCh. 14.3 - Prob. 17MCCh. 14.3A - In the following figures, describe a sequence of...Ch. 14.3A - Prob. 2ACh. 14.3A - In each of the following drawings, find...Ch. 14.3A - Prob. 4ACh. 14.3A - AB is the image of a candle AB produced by a box...Ch. 14.3A - Prob. 6ACh. 14.3A - Prob. 7ACh. 14.3A - Prob. 8ACh. 14.3A - Prob. 9ACh. 14.3A - Prob. 10ACh. 14.3A - Prob. 11ACh. 14.3A - Prob. 12ACh. 14.3A - Prob. 13ACh. 14.3B - Prob. 1ACh. 14.3B - Prob. 2ACh. 14.3B - Prob. 4ACh. 14.3B - Prob. 5ACh. 14.3B - Prob. 6ACh. 14.3B - Prob. 7ACh. 14.3B - Prob. 8ACh. 14.3B - Prob. 9ACh. 14.3B - Prob. 11ACh. 14.3B - Prob. 12ACh. 14.3B - Prob. 13ACh. 14.CR - Prob. 1CRCh. 14.CR - Prob. 2CRCh. 14.CR - Prob. 3CRCh. 14.CR - Prob. 4CRCh. 14.CR - Given that STAR in the figure shown is a...Ch. 14.CR - Prob. 6CRCh. 14.CR - Given that SNOSWO in the following figure,...Ch. 14.CR - Prob. 8CRCh. 14.CR - Prob. 9CRCh. 14.CR - Prob. 10CRCh. 14.CR - If a translation determined by (x,y)(x+3,y2) is...Ch. 14.CR - Prob. 12CRCh. 14.CR - Prob. 13CRCh. 14.CR - On a 1-m equilateral triangle pool table, a ball...Ch. 14.CR - Prob. 15CRCh. 14.CR - Prob. 16CRCh. 14.CR - Prob. 17CRCh. 14.CR - Prob. 18CRCh. 14.CR - Prob. 19CRCh. 14.CR - Prob. 21CRCh. 14.CR - Prob. 22CRCh. 14.CR - Prob. 23CRCh. 14.CR - Prob. 24CRCh. 14.CR - Prob. 25CRCh. 14.CR - Prob. 26CRCh. 14.CR - What dilation, if any, allows a line with equation...Ch. 14 - Prob. 1NT
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Simply:(p/(x-a))-(p/(x+a))arrow_forwardMake M the subject: P=2R(M/√M-R)arrow_forwardExercice 2: Soit & l'ensemble des nombres réels. Partie A Soit g la fonction définie et dérivable sur R telle que, pour tout réel x. g(x) = - 2x ^ 3 + x ^ 2 - 1 1. a) Étudier les variations de la fonction g b) Déterminer les limites de la fonction gen -oo et en +00. 2. Démontrer que l'équation g(x) = 0 admet une unique solution dans R, notée a, et que a appartient à | - 1 ;0|. 3. En déduire le signe de g sur R. Partie B Soit ƒ la fonction définie et dérivable sur R telle que, pour tout réel s. f(x) = (1 + x + x ^ 2 + x ^ 3) * e ^ (- 2x + 1) On note f la fonction dérivée de la fonction ƒ sur R. 1. Démontrer que lim x -> ∞ f(x) = - ∞ 2. a) Démontrer que, pour tout x > 1 1 < x < x ^ 2 < x ^ 3 b) En déduire que, pour x > 1 0 < f(x) < 4x ^ 3 * e ^ (- 2x + 1) c) On admet que, pour tout entier naturel n. lim x -> ∞ x ^ n * e ^ (- x) = 0 Vérifier que, pour tout réel x, 4x ^ 3 * e ^ (- 2x + 1) = e/2 * (2x) ^ 3 * e ^ (-2x) puis montrer que: lim x -> ∞ 4x ^ 3 * e…arrow_forward
- Please explain the pass-to-passarrow_forwardMinistry of Higher Education & Scientific Research Babylon University College of Engineering - Al musayab Automobile Department Subject :Engineering Analysis Time: 2 hour Date:27-11-2022 کورس اول تحليلات تعمیر ) 1st month exam / 1st semester (2022-2023)/11/27 Note: Answer all questions,all questions have same degree. Q1/: Find the following for three only. 1- 4s C-1 (+2-3)2 (219) 3.0 (6+1)) (+3+5) (82+28-3),2- ,3- 2-1 4- Q2/:Determine the Laplace transform of the function t sint. Q3/: Find the Laplace transform of 1, 0≤t<2, -2t+1, 2≤t<3, f(t) = 3t, t-1, 3≤t 5, t≥ 5 Q4: Find the Fourier series corresponding to the function 0 -5arrow_forwardQ1lal Let X be an arbitrary infinite set and let r the family of all subsets F of X which do not contain a particular point x, EX and the complements F of all finite subsets F of X show that (X.r) is a topology. bl The nbhd system N(x) at x in a topological space X has the following properties NO- N(x) for any xX N1- If N EN(x) then x€N N2- If NEN(x), NCM then MeN(x) N3- If NEN(x), MEN(x) then NOMEN(x) N4- If N = N(x) then 3M = N(x) such that MCN then MeN(y) for any уем Show that there exist a unique topology τ on X. Q2\a\let (X,r) be the topology space and BST show that ẞ is base for a topology on X iff for any G open set xEG then there exist A Eẞ such that x E ACG. b\Let ẞ is a collection of open sets in X show that is base for a topology on X iff for each xex the collection B, (BEB\xEB) is is a nbhd base at x. - Q31 Choose only two: al Let A be a subspace of a space X show that FCA is closed iff F KOA, K is closed set in X. الرياضيات b\ Let X and Y be two topological space and f:X -…arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
Algebra for College StudentsAlgebraISBN:9781285195780Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Algebra for College Students
Algebra
ISBN:9781285195780
Author:Jerome E. Kaufmann, Karen L. Schwitters
Publisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Area Between The Curve Problem No 1 - Applications Of Definite Integration - Diploma Maths II; Author: Ekeeda;https://www.youtube.com/watch?v=q3ZU0GnGaxA;License: Standard YouTube License, CC-BY