Chapter 14, Problem 9PA

Sub part (a):

To determine

Diminishing marginal utility.

Explanation of Solution

The utility function is ${\text{W}}^{\frac{1}{2}}$. Since the power function is less than one, the marginal utility will be diminishing. It implies that the person is risk averse.

Figure 1 illustrates the diminishing marginal utility.

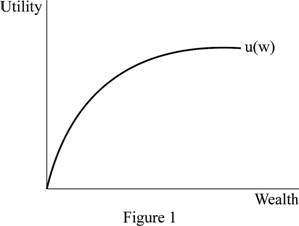
In Figure 1, the horizontal axis measures the quantity of wealth and the vertical axis measures the utility. When the quantity of wealth increases then the additional utility decreases.

Economics Concept Introduction

Concept introduction:

Marginal utility: Marginal utility refers to the additional units of satisfaction derived from one more additional unit of goods and services.

Diminishing marginal utility: Diminishing marginal utility refers to a decrease in the additional satisfaction as a result of increasing the consumption.

Sub Part (b):

To determine

Expected value.

Explanation of Solution

Since the value is sure, the probability is 1. Expected value of A can be calculated as follows:

$\begin{array}{c}\text{Expected value}=\text{Probability}\times \text{Wealth}\\ =1\times 4,000,000\\ =4,000,000\end{array}$

Expected value of A is $4,000,000.

Expected value of B can be calculated as follows.

$\begin{array}{c}\text{Expected value}=\left({\text{Probability}}_1\times {\text{Wealth}}_1\right)+\left({\text{Probability}}_2\times {\text{Wealth}}_2\right)\\ =\left(0.6\times 1,000,000\right)+\left(0.4\times 9,000,000\right)\\ =600,000+3,600,000\\ =4,200,000\end{array}$

Expected value of B is $4,200,000. Thus, B offers higher value.

Economics Concept Introduction

Concept introduction:

Risk is the future uncertainty about deviation from expected earnings or expected outcome. Risk measures the uncertainty situation that an investor is willing to take to realize a gain from an investment.

Risk aversion: Risk aversion can be defined as it is a dislike of an uncertainty.

Marginal utility: Marginal utility refers to the additional units of satisfaction derived from one more additional unit of goods and services.

Diminishing marginal utility: Diminishing marginal utility refers to a decrease in the additional satisfaction as a result of increasing the consumption.

Sub part (c):

To determine

Expected utility.

Explanation of Solution

Expected utility of A can be calculated as follows:

$\begin{array}{c}\text{Expected value}={\text{Wealth}}^{\frac{1}{2}}\\ =4,000,{000}^{\frac{1}{2}}\\ =2,000\end{array}$

Expected utility of A is $2,000.

Expected utility of B can be calculated as follows.

$\begin{array}{c}\text{Expected value}=\left({\text{Probability}}_1\times {\text{Wealth}}_1^{\frac{1}{2}}\right)+\left({\text{Probability}}_2\times {\text{Wealth}}_2^{\frac{1}{2}}\right)\\ =\left(0.6\times 1,000,{000}^{\frac{1}{2}}\right)+\left(0.4\times 9,000,{000}^{\frac{1}{2}}\right)\\ =\left(0.6\times 1,000\right)+\left(0.4\times 3,000\right)\\ =600+1,200\\ =1,800\end{array}$

Expected utility of B is $1,800.

Economics Concept Introduction

Concept introduction:

Risk is the future uncertainty about deviation from expected earnings or expected outcome. Risk measures the uncertainty situation that an investor is willing to take to realize a gain from an investment.

Risk aversion: Risk aversion can be defined as it is a dislike of an uncertainty.

Marginal utility: Marginal utility refers to the additional units of satisfaction derived from one more additional unit of goods and services.

Diminishing marginal utility: Diminishing marginal utility refers to a decrease in the additional satisfaction as a result of increasing the consumption.

Sub part (d):

To determine

greaterExpected utility.

Explanation of Solution

Since the expected utility from B is greater than A, the person should select A.

Economics Concept Introduction

Concept introduction:

Risk is the future uncertainty about deviation from expected earnings or expected outcome. Risk measures the uncertainty situation that an investor is willing to take to realize a gain from an investment.

Risk aversion: Risk aversion can be defined as it is a dislike of an uncertainty.

Marginal utility: Marginal utility refers to the additional units of satisfaction derived from one more additional unit of goods and services.

Diminishing marginal utility: Diminishing marginal utility refers to a decrease in the additional satisfaction as a result of increasing the consumption.