Chapter 14, Problem 8P

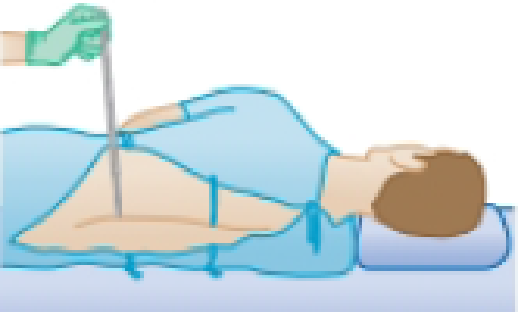
The human brain and spinal cord are immersed in the cerebrospinal fluid. The fluid is normally continuous between the cranial and spinal cavities and exerts a pressure of 100 to 200 mm of H₂O above the prevailing atmospheric pressure. In medical work, pressures are often measured in units of millimeters of H₂O because body fluids, including the cerebrospinal fluid, typically have the same density as water. The pressure of the cerebrospinal fluid can be measured by means of a spinal tap as illustrated in Figure P14.8. A hollow tube is inserted into the spinal column, and the height to which the fluid rises is observed. If the fluid rises to a height of 160 mm, we write its gauge pressure as 160 mm H₂O. (a) Express this pressure in pascals, in atmospheres, and in millimeters of mercury. (b) Some conditions that block or inhibit the flow of cerebrospinal fluid can be investigated by means of Queckenstedt’s test. In this procedure, the veins in the patient’s neck are compressed to make the blood pressure rise in the brain, which in turn should be transmitted to the cerebrospinal fluid. Explain how the level of fluid in the spinal tap can be used as a diagnostic tool for the condition of the patient’s spine.

Figure P14.8