
(a)
Design a circuit which produces a transfer function of
(a)
Explanation of Solution
Problem design:
Synthesize a circuit that will yield the transfer function
Calculation:
The transfer function of the circuit is,
The above equation is written as,
For the above transfer function, it has two repeated zeros at
The Figure 14.39 (b) in the textbook, that shows a cascade two stages of the circuit with a zero at
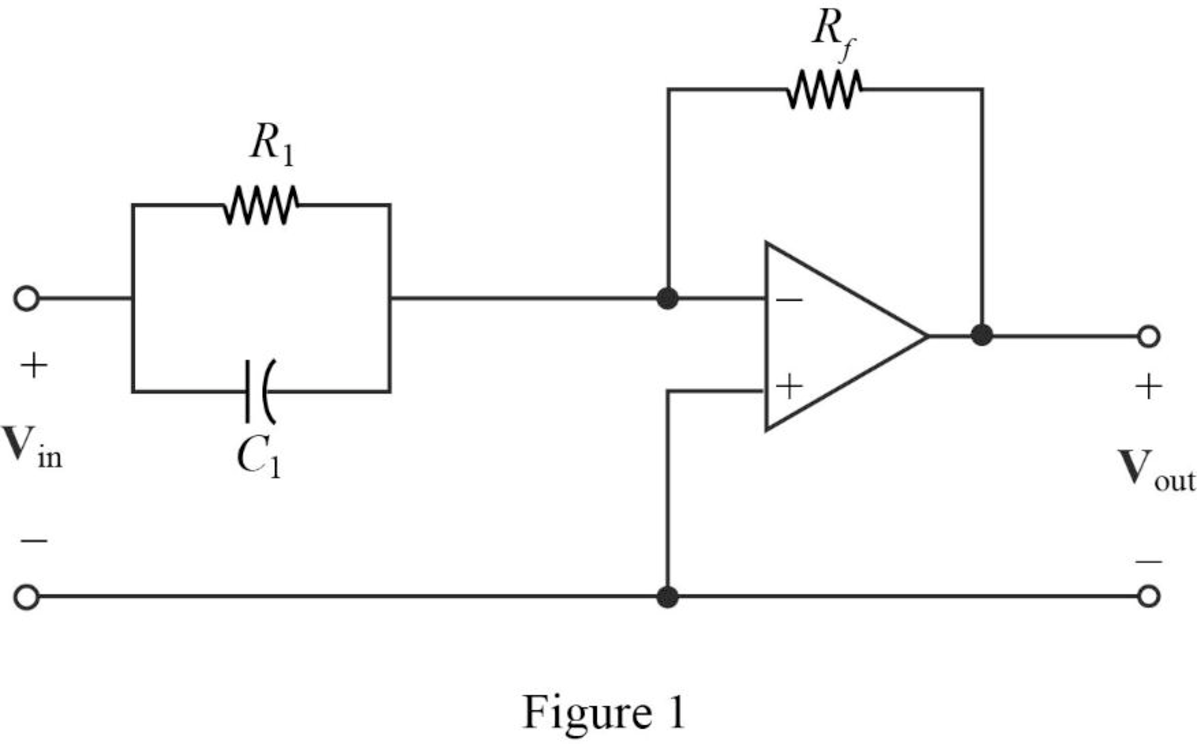
For a single zero,
Substitute
Let arbitrarily consider
Substitute
Transfer function:
The input impedance of the cascaded circuit is,
Then, write the Formula for the transfer function for the cascaded two stage amplifier.
Substitute
Thus, consider that the transfer function for
Substitute 1 for
Completing the design by letting
Since, two repeated zeros at
Therefore,
Substitute
Thus, the final design of the circuit is,
Conclusion:
Thus, a circuit is designed which produces a transfer function of
(b)
Design a circuit which produces a transfer function of
(b)
Explanation of Solution
Problem design:
Synthesize a circuit that will yield the transfer function
Calculation:
The transfer function of the circuit is,
Consider the transfer function for the cascaded circuit as below.
The above transfer function, it has two poles at
The Figure 14.39 (a) in the textbook, that shows a cascade two stages of the circuit with pole at
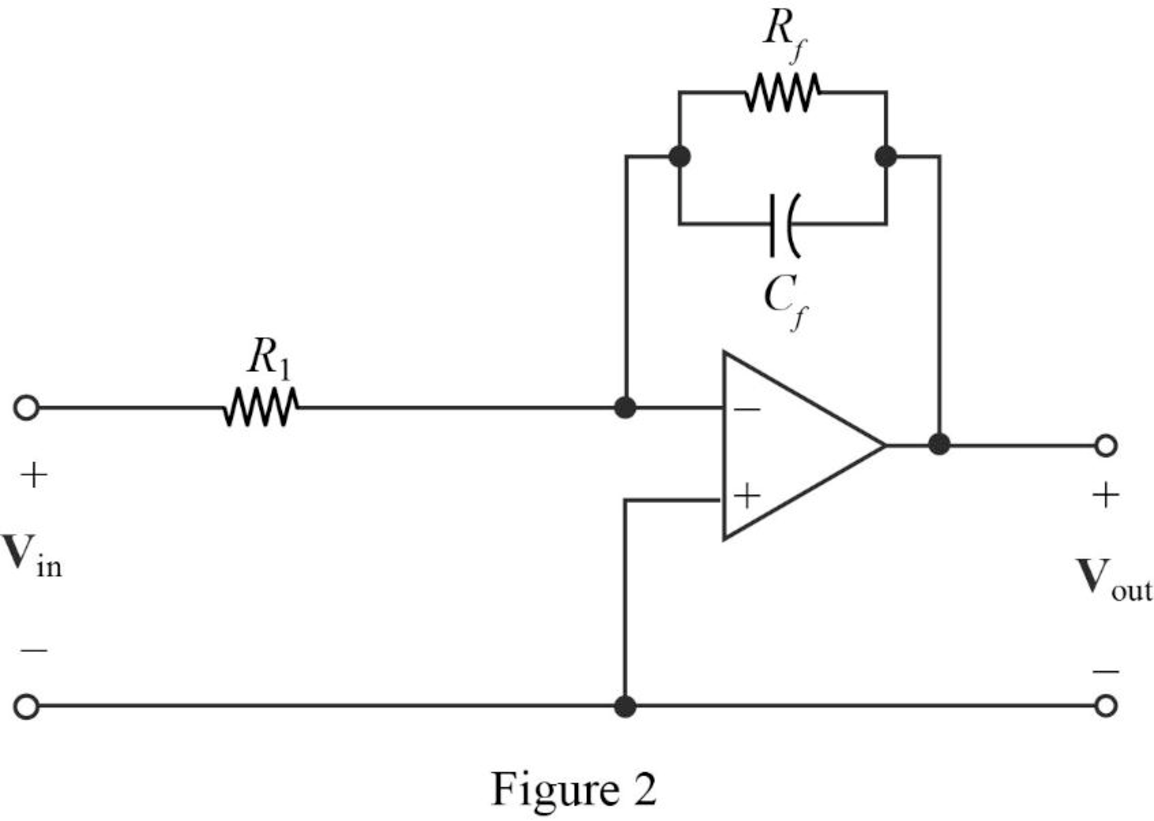
The above Figure 2, is the representation for the first stage and second stage of a cascaded circuit to be drawn.
Consider the denominator of given transfer function and the first pole as
Where,
Substitute
Let arbitrarily consider
Substitute
Transfer function:
Find the feedback impedance of the cascaded circuit in Figure 2.
Write the formula for the transfer function of the cascaded circuit in Figure 2 as follows
Substitute
Therefore, consider the transfer function for the first pole
Substitute 500 for
Completing the design by letting
Consider the denominator of given transfer function and the first pole as
Where,
Substitute
Arbitrarily consider
Substitute
Therefore, consider the transfer function for the second pole
Substitute 100 for
Completing the design by letting
Then, from the transfer function of the two stages write the complete transfer function as follows.
Substitute
Thus, the final design of the circuit is,
Conclusion:
Thus, a circuit is designed which produces a transfer function of
Want to see more full solutions like this?
Chapter 14 Solutions
ENGINEERING CIRCUIT...(LL)>CUSTOM PKG.<
- Suppose we have the following transfer function: K(s² – 10s + 1) 2s4 + 4s3 – s + 11 + K` Gp(8) a. Express the system in state-space form. b. Translate the state-space form into block diagram format.arrow_forwardPlease explain with details on why. Thank you.arrow_forwardClassify the response of the system and write ihe transfer function of the step response: (t) = A+ Be 161 cos(12t + p) %3Darrow_forward
- Crossover/damped vs. damping ratio A second order system is define as: 1.3000 1.2000 R(s) k C(s) 1.1000 s(s + 23wn) 1.0000 0.9000 k 0.8000 1) What is the closed loop transfer function? 0.7000 0.0 0.2 0.4 0.6 0.8 1.0 2) What is the open loop transfer function? Phase Margin vs. damping ratio 90.0 80.0 1007 3) Using the open-loop transfer function, derive an equation for the ratio w/w. where c indicates the unity gain crossover frequency and d indicates the damped natural frequency. Plot the results for a damping ratio of 0 to .9 70.0 60.0 50.0 40.0 30.0 4) Using the open-loop transfer function, derive an equation for the phase margin at the crossover frequency. Plot the results for a damping ratio of 0 to .9 20.0 10.0 0.0 0.0 0.2 0.4 0.4 0.6 0.8 1.0arrow_forwardb) The unit step response of a first order system is shown below: Develop the transfer function of this system. Please include detailed steps. Hint: Please find the time constant and the constant gain (the numerator).arrow_forward2s-0.45 14, The system, having its transfer function H(s) = is considered as: A. Marginally Stable B. Stable C. Unstable D. Stability cannot be defined 8. | 4arrow_forward
- A system transfer function is given as: What is the DC gain of the system H(s) = 250 0.01(s+50)arrow_forwardPlease don't provide handwritten solution .... ...arrow_forward2. Consider the following transfer function model W(s) = 1 s5 +10s +35³ +50s² +24s +11 Use the Hurwitz criterion to determine if the closed-loop system is stable: W(s)arrow_forward
- Given the circuit below, with R=2 ohms and C=0.2 Farads, compute for the transfer function Vo(s)/Vin(s). Express your answers in 2 decimal places. Vin (t) i(t) vo(t) R Fill in the blanks the numerical coefficients to the TF shown below that corresponds to A , & D V.(8) Vin (s) As+Bs Cs+Ds+1 B.arrow_forwardPlease help and explain the answer. NEED ASAP.arrow_forwardDetermine a) The transfer function H(s) = Vo(s) / lo(s) for the circuit shown below b) Find the zeroes and the poles of this transfer function. T, (s) www. 3s Vo(s)arrow_forward
 Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON
Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning
Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education
Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON
Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,
Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,





