Chapter 13.P, Problem 4P

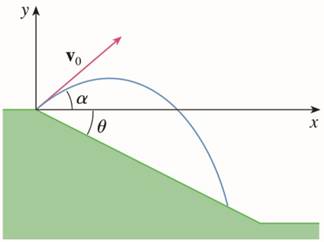
(a) A projectile is fired from the origin down an inclined plane that makes an angle $\theta$ with the horizontal. The angle of elevation of the gun and the initial speed of the projectile are $\alpha$ and ${\nu }_0$, respectively. Find the position vector of the projectile and the parametric equations of the path of the projectile as functions of the time t. (Ignore air resistance.)

(b) Show that the angle of elevation $\alpha$ that will maximize the downhill range is the angle halfway between the plane and the vertical.

(c) Suppose the projectile is fired up an inclined plane whose angle of inclination is $\theta$. Show that, in order to maximize the (uphill) range, the projectile should be fired in the direction halfway between the plane and the vertical.

(d) In a paper presented in 1686, Edmond Halley summarized the laws of gravity and projectile motion and applied them to gunnery. One problem he posed involved firing a projectile to hit a target a distance R up an inclined plane. Show that the angle at which the projectile should be fired to hit the target but use the least amount of energy is the same as the angle in part (c). (Use the fact that the energy needed to fire the projectile is proportional to the square of the initial speed, so minimizing the energy is equivalent to minimizing the initial speed.)